4.2.4　矩阵的逆

4.2.4　矩阵的逆

如果B∗A＝A∗B＝E，那么矩阵A的逆矩阵为B，那么，即一个矩阵和它的逆矩阵左乘或者右乘结果都是单位矩阵.易知，只有方阵才具有逆矩阵.MATLAB中可以通过函数inv求矩阵的逆.

矩阵的逆在求解线性方程组时是重要的，对于一般的给定线性方程组A∗X＝b，其解就可以通过X＝inv（A）b求得.

例4.3　求方阵的逆矩阵，验证A与A-1是否是互逆的；求解线性方程组.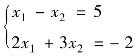

解：

上述计算中可见A⋅B＝B⋅A，即A⋅A-1＝A-1⋅A，故A与A-1是互逆的.需要注意的是，对于严重病态的矩阵或奇异矩阵，inv求解时会出警告提示，因为这时候其逆矩阵本来就不存在，或者非常容易受扰动而使求解不精确，例如：

如果矩阵A不是一个方阵，或者A是一个非满秩的方阵，矩阵A没有逆矩阵，但可以找到一个与A的转置矩阵同型的矩阵B，使得：

A⋅B⋅A＝A

B⋅A⋅B＝B

此时称矩阵B为矩阵A的伪逆，也称为广义逆矩阵.在MATLAB中，求一个矩阵伪逆的函数是pinv（A）.例如，对上述A：