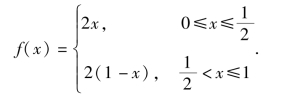7.2.3 分类结果确定及分析
依据最大隶属度原则，预设分类判定阈值λ＝0.7，若待分类样本的隶属度函数φ（vi）>λ，则对该样本进行分类识别，且将样本归为φ（vi）值最大的那一类.每次识别完成后，将识别类加入训练样本集，并重新计算聚类中心，从而形成新的分类模式.
利用上面设计的分类器，取每类样本的前30个样本作为训练样本集，得到4个聚类中心：（0.712 305，0.164 326）、（0.606 750，0.220 935）、（0.307 802，0.110 198）、（1.004 579，0.365 064）.程序如下：
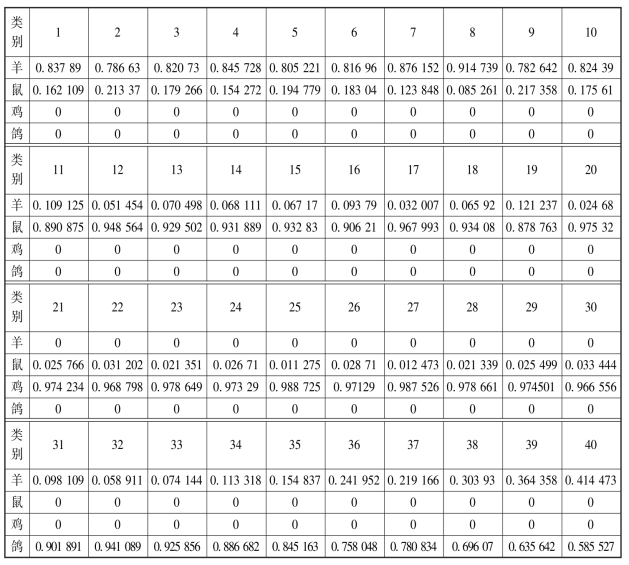
取每类样本的十个样本作为识别样本，得到每个样本对各类的隶属度，见表7-5（其中1～10为羊、11～20为鼠、21～30为鸡、31～40为鸽）.程序如下：
表7-5 每个样本对各类的隶属度
由以上数据可得，分类器对四种样品全血光谱数据的分类正确识别率见表7-6.
表7-6 分类器对四种样品全血光谱数据的分类正确识别率 %
可知，基于MATLAB程序设计的模糊模式分类器及隶属函数，对动物血液发射光谱的识别达到了令人满意的效果.
第7章练习题
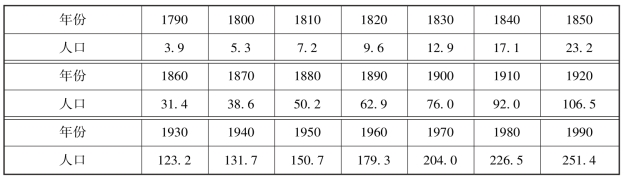
1.1790—1990年间美国每隔10年的人口记录见表7-7.
表7-7 1790—1990年间美国每隔10年的人口记录 ×106
用以上数据检验马尔萨斯（Malthus）人口指数增长模型，根据检验结果进一步讨论马尔萨斯人口模型的改进，并利用至少两种模型来预测美国2010年的人口数量.
提示1：Malthus模型的基本假设是：人口的增长率为常数，记为r，记时刻t的人口为x（t）（即x（t）为模型的状态变量），且初始时刻的人口为x0，于是得到如下微分方程：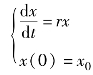
.
提示2：阻滞增长模型（或Logistic模型）由于资源、环境等因素对人口增长的阻滞作用，人口增长到一定数量后，增长率会下降.假设人口的增长率为x的减函数，如设r（x）＝r（1-x/xm），其中r为固有增长率（x很小时），xm为人口容量（资源、环境能容纳的最大数量），于是得到如下微分方程：
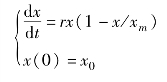
2.对于迭代方程
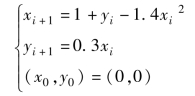
先编写求解方程的函数文件，然后调用该函数文件求30 000个点上的x、y，最后在所有的（xi，yi）坐标处标记一个点（不要连线）绘出图形，这种图形又称为埃农（Henon）引力线图，它将迭代出来的随机点吸引到一起，最后得出貌似连贯的引力线图.
3.有一周期为4π的正弦波上叠加了方差为0.1的正态分布的随机噪声的信号，用循环结构编制一个三点线性滑动平均的程序.
提示：①用0.1∗randn（1，n）产生方差为0.1的正态分布的随机噪声；②三点线性滑动平均就是依次取每三个相邻数的平均值作为新的数据，如x1（2）＝（x（1）＋x（2）＋x（3））/3，x1（3）＝（x（2）＋x（3）＋x（4））/3，….
4.编写一段程序，能够把输入的摄氏温度转化成华氏温度，也能把华氏温度转换成摄氏温度，实现如图7-12所示的功能.
图7-12 习题4图
提示：摄氏温度＝（华氏温度-32）×5/9.
5.利用迭代思想解决问题：
（1）求出分式线性函数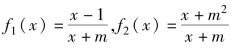
的不动点，再编程判断它们的迭代序列是否收敛.
（2）下面函数的迭代是否会产生混沌？
