5.2.2 二重积分与三重积分计算
一、二重积分
函数f(x,y)在有界闭区域D上的二重积分定义为
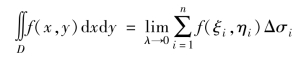
其中,Δσ1,Δσ2,…,Δσn是由区域D任意分割成的n个小闭区域,同时也表示它们的面积;(ξi,ηi)∈Δσi,i=1,2,…,n;![]() .
.
设积分区域D可以用不等式
φ1(x)≤y≤φ2(x),a≤x≤b
来表示(如图5-5(a)所示),则上述二重积分可以化为如下累次积分
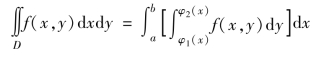
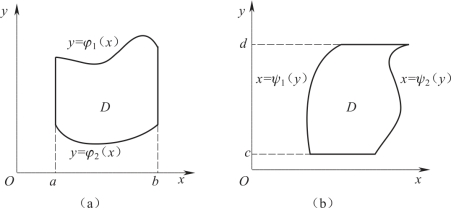
图5-5 X型和Y型区域
类似地,如果积分区域D可以用不等式
ψ1(y)≤x≤ψ2(y),c≤y≤d
来表示(如图5-5(b)所示),则上述二重积分可以化为如下累次积分
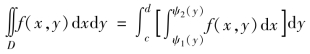
1.二重积分符号解
将二重积分化为累次积分后,可以通过嵌套调用MATLAB提供的int函数来求解二重积分.
例5.10 求下列二重积分.
①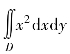 ,其中D是由抛物线y=x2和y=2-x2所围成的区域;
,其中D是由抛物线y=x2和y=2-x2所围成的区域;
②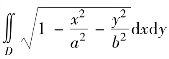 ,其中D是由椭圆
,其中D是由椭圆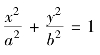 所围成的区域,a>0,b>0.
所围成的区域,a>0,b>0.
解:
①首先,绘制积分区域D.
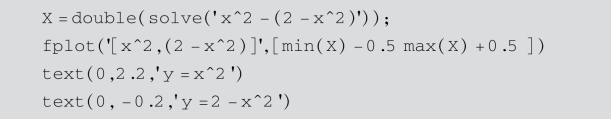
运行结果如图5-6所示.
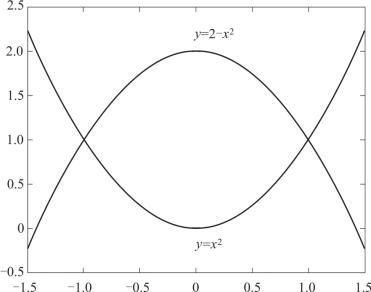
图5-6 二重积分区域示意图
然后,观察积分区域示意图,可知积分区域为
![]()
最后,计算该二重积分:
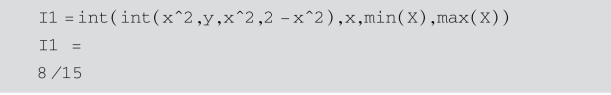
②若直接在直角坐标系中计算该二重积分比较麻烦,考虑做如下广义极坐标变换
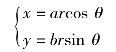
其中,r≥0;0≤θ≤2π.在该变换下,积分区域化为
![]()
编写如下语句计算该二重积分:

2.二重积分数值解
MATLAB提供了函数quad2d来计算一般区域上二重积分的数值解,该函数的调用格式为
![]()
其中,fun是被积函数的符号表达式、内联函数、匿名函数或M函数;[a,b]×[c(x),d(x)]构成积分区域;param1,val1,param2,val2,…是可选的参数名及参数值;I是返回的数值积分值.
例5.11 求解二重积分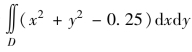 ,其中D是由单位圆x2+y2≤1所围成的区域.
,其中D是由单位圆x2+y2≤1所围成的区域.
解:积分区域D为
![]()
(1)符号积分法
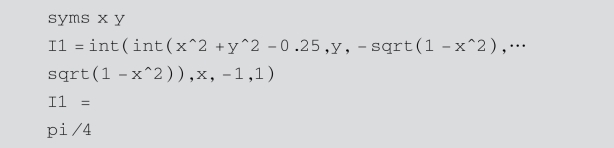
(2)数值积分法

二、三重积分
函数f(x,y,z)在空间有界闭区域Ω上的三重积分定义为
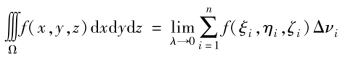 (https://www.daowen.com)
(https://www.daowen.com)
其中,Δν1,Δν2,…,Δνn是由区域Ω任意分割成的n个小闭区域,同时也表示它们的体积;(ξi,ηi,ζi)∈Δνi,i=1,2,…,n;![]() .
.
1.三重积分符号解
与二重积分类似,可以将三重积分化为累次积分后,通过嵌套调用MATLAB提供的int函数来求解三重积分.
例5.12 计算三重积分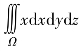 ,其中Ω由曲面z=xy、平面x+y+z=1及平面z=0所围成.
,其中Ω由曲面z=xy、平面x+y+z=1及平面z=0所围成.
解:
首先,绘制积分区域Ω:

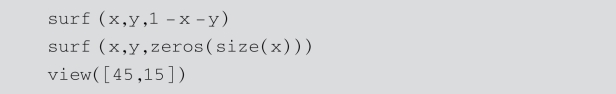
运行结果如图5-7所示.
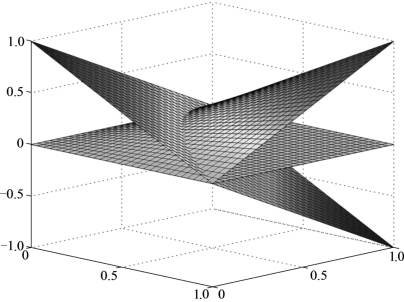
图5-7 三重积分区域示意图
然后,观察积分区域示意图,可以发现积分区域为
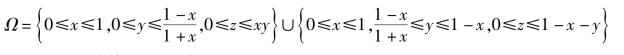
最后,计算三重积分:

例5.13 计算三重积分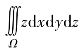 ,其中Ω为曲面
,其中Ω为曲面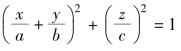 在第一卦限的部分,其中,a>0,b>0,c>0.
在第一卦限的部分,其中,a>0,b>0,c>0.
解:
(1)直角坐标系法
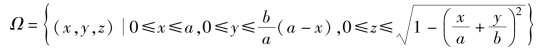

(2)广义柱坐标系法
令x=arcosθ,y=brsinθ,z=z,则
![]()

(3)广义球坐标系法
令x=arsinφcosθ,y=brsinφsinθ,z=z,则
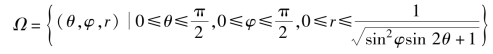


2.三重积分数值解
MATLAB提供了函数triplequad来求解长方体区域上三重积分的数值解,该函数调用格式为
![]()
其中,fun是被积函数的字符表达式、内联函数、匿名函数或M函数;[a,b]×[c,d]×[e,f]构成长方体积分区域;tol是指定的误差限(默认值为10-6);method为选择使用的求解一元定积分的数值函数(默认为@quadl,也可以选择@quad,甚至是用户自己编写的数值积分求解函数);I是返回的数值积分值.
例5.14 计算三重积分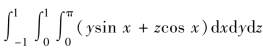 .
.
解:

MATLAB目前没有提供专门的用来求解一般区域上三重积分数值解的函数,但是可以将三重积分化为累次积分后,通过嵌套调用quad和quad2d函数来求解三重积分的数值解.现分别给出三重积分相应的三种累次积分形式的MATLAB语句格式,见表5-1.
表5-1 一般区域上三重积分的数值求解方法

续表

例5.15 计算三重积分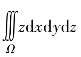 的数值解,其中Ω为曲面
的数值解,其中Ω为曲面![]()
![]() 在第一卦限的部分.
在第一卦限的部分.
解:
(1)先一后二

(2)先二后一

(3)三次定积分

