5.4.1 常微分方程的运算
1.常微分方程符号解运算
微分方程中所出现的未知函数的最高阶导数的阶数叫作微分方程的阶.n阶常微分方程的一般形式为
F(x，y，y′，y″，…，y(n))＝0
设函数y＝f（x）在区间I上有n阶连续导数，如果在区间I上，有
F(x，f(x)，f′(x)，f″(x)，…，f(x)(n))≡0
则称函数y＝f（x）为微分方程F（x，y，y′，y″，…，y（n））＝0在区间I上的解.
如果微分方程的解中含有任意常数，且任意常数的个数与微分方程的阶数相同，则称这样的解为微分方程的通解.如果根据一定的条件确定了通解中的任意常数，就可以得到微分方程的特解.
微分方程的解的图形是一条曲线，称为微分方程的积分曲线.
MATLAB提供了dsolve函数求解常微分方程（组）.该函数允许用字符串的形式描述微分方程及指定的边界或初始条件，然后给出微分方程的符号解（解析解）.该函数的一般调用格式为
其中，‘eqn1，…，eqnN’是微分方程（组）的符号表达式；‘cond1，…，condN’是指定的边界或初始条件；‘v’是常微分方程（组）中指定的符号自变量，其默认值为‘t’；Y是返回的符号解.
在微分方程（组）的符号表达式中，大写的字母D表示对自变量的微分算子，微分算子D后面的数字表示微分的阶数，而字母则表示因变量，即待求解的未知函数，例如，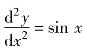
可以写为D2y＝sin（x）.
初始条件和边界条件的表达式类似，例如，y′（a）＝b可以写为Dy（a）＝b.
当初始条件和边界条件的个数少于微分方程的阶数时，在所求的符号解Y中将出现任意常数符号C1、C2等.
例5.30 求二阶微分方程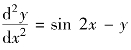
的通解及在条件y（0）＝0，y′（π）＝0下的特解.
解：
运行结果如图5-11所示.
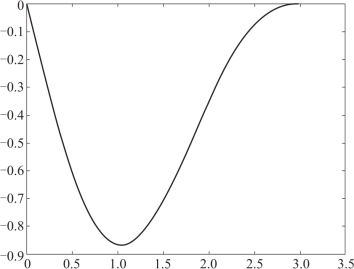
图5-11 微分方程符号解的积分曲线
2.常微分方程初值问题数值解运算
求n阶微分方程F（x，y，y′，y″，…，y（n））＝0满足条件
的特解的这样一个问题，称为n阶微分方程的初值问题.
MATLAB提供了一系列用来求解微分方程初值问题数值解的函数，包括ode系列函数ode45、ode23、ode15s、ode23s、ode15i等，它们所解决的常微分方程的问题类型、精度和所用算法见表5-2.
表5-2 常微分方程初值问题解算指令比较
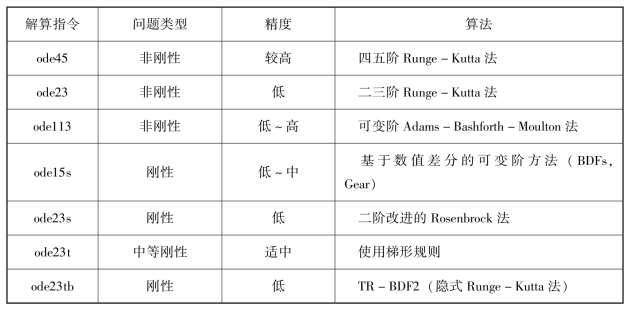
上述解算器的一般调用格式为
[T，Y]＝odesolver(odefun，tspan，y0，options，p1，p2，…)
各个参数的解释如下：
odefun：微分方程的MATLAB语言描述函数，必须是函数句柄或者字符串，且必须写成MATLAB规范格式，即一阶显式微分方程（组）形式.
tspan：给出变量的求解区间，当tspan表示二元向量[t0，tf]时，tspan用来给出求解数值解的时间区间；当tspan表示多元向量[t0，t1，…，tf]时，给出tspan定义的时间点上的数值解.注意后者tspan必须严格单调.
y0：初值条件，依次输入所有状态变量的初值.
options：微分方程的优化参数，使用odeset可以设置具体参数，详细内容查看MATLAB的帮助文档.
T：所求数值解的自变量列向量，也就是odesolver计算微分方程的值的点.
Y：所求微分方程的因变量矩阵，第i列表示第i个状态变量的值，行数与T的一致.
应用odesolver解算器求解常微分方程初值问题数值解的一般求解过程为：
（1）将待求问题化为标准形式
如果微分方程由一个或多个高阶微分方程给出，应先将其变换成一阶显式常微分方程组，这只需为每一个因变量除最高阶外的每一阶微分式选择一个状态变量即可，具体做法参考下面的例子.
（2）编写微分方程的描述函数
微分方程的描述可以是函数句柄、字符表达式，也可以是一个单独的MATLAB函数文件.作为整个求解程序的一个子函数，MATLAB提供了odefile的模板，采用type odefile命令显示其详细内容，然后将其复制到脚本编辑窗口，在合适的位置填入所需内容即可.
（3）选择合适的解算指令求解问题
根据微分方程问题所要求的求解精度与速度及微分方程是否为刚性方程等要求，参照表5-2的介绍选择合适的解算指令来求解常微分方程的初值问题.
例5.31 求二阶微分方程y″＋3y＝4sin 8t在区间[0，6]上的解，初始条件为y（0）＝0，y′（0）＝1.
解：令y1＝y，y2＝y′，则所求高阶微分方程可以转化为如下的一阶微分方程组
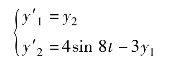
编写如下语句：
运行结果如图5-12所示.
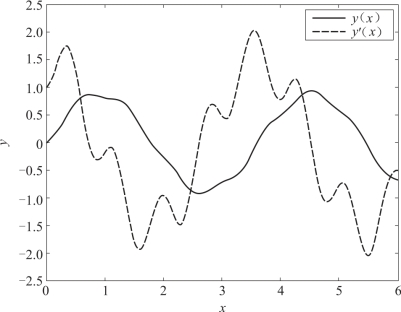
图5-12 微分方程初值问题数值解的积分曲线
例5.32 已知阿波罗卫星的运动轨迹满足下面的微分方程：
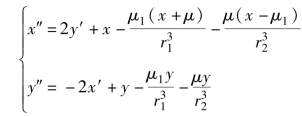
其中，
，x（0）＝1.2，x′（0）＝0，y（0）＝0，y′（0）＝-1.049 357 51，试绘制阿波罗卫星的运动轨迹图.
解：令u1＝x，u2＝x′，u3＝y，u4＝y′，则将所求高阶微分方程组转化为如下的一阶微分方程组
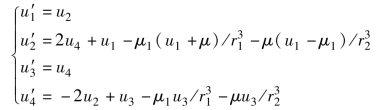
编写如下语句：
运行结果如图5-13所示.
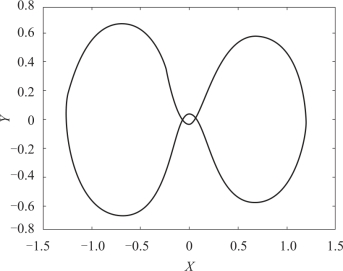
图5-13 阿波罗卫星运动轨迹
3.常微分方程边值问题数值解运算
对n阶微分方程F（x，y，y′，y″，…，y（n））＝0，如果能在不同的两点a和b处，唯一刻画n个附加条件φ[y（a），y（b）]＝0，并且在区间a≤t≤b上求解该微分方程，则称此问题为n阶微分方程的边值问题.
MATLAB提供了bvp4c和bvp5c函数来求解微分方程边值问题的数值解，它们的使用方法类似，这里仅以bvp4c函数为例给出求解常微分方程边值问题数值解的一般求解过程.
（1）微分方程与边值条件的MATLAB描述
微分方程函数的描述与初值问题情形完全类似，边值条件函数描述出φ[y（a），y（b）]＝0中的各个表达式即可.
（2）初始化参数
调用bvpinit函数生成bvp系列函数所必需的猜测数据网格，该函数的调用格式为
其中，x是初始网格点的估计值；yinit是数值解的初始猜测值；[anew，bnew]用于扩展解sol的范围；parameters是其他未知参数；solinit返回猜测数据网格，其中solinit.x为初始网格点，solinit.y给出网格点上微分方程解的猜测值，solinit.y（：，i）表示节点solinit.x（i）处的解的猜测值.
（3）求解边值问题
直接调用函数bvp4c求解边值问题，其一般调用格式为
这里，odefun是微分方程的描述函数；bcfun是边值条件的描述函数；solinit为生成的猜测数据网格；options是微分方程的优化参数.返回值中，sol.x是指令bvp4c所采用的网格节点；sol.y是y（x）在sol.x网点上的近似解值；sol.yp是y′（x）在sol.x网点上的近似解值；sol.parameters是微分方程所包含的未知参数的近似解值，当所求微分方程包含未知参数时，该域存在.
例5.33 求解边值问题
边值条件为y（0）＝0，y（4）＝-2.
解：令y1＝y，y2＝y′，则所求高阶微分方程可以转化为如下一阶微分方程组
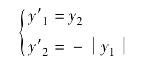
编写如下语句：
运行结果如图5-14所示.
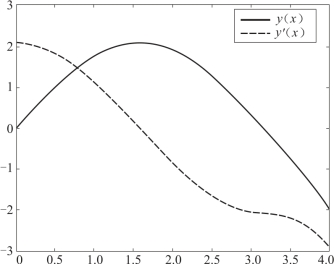
图5-14 微分方程边值问题数值解的积分曲线