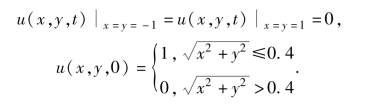5.4.2 偏微分方程的运算
1.一般偏微分方程的数值解运算
MATLAB语言提供了pdepe函数,可以直接求解一般的偏微分方程(组),它的调用格式为:
sol=pdepe(m,@pdefun,@icfun,@bcfun,xmesh,tspan)
参数说明:
m:与方程的对称性有关的一个参数,取值为0、1或2.
@pdefun:是偏微分方程(组)的描述函数,必须先将微分方程转换成下面的标准形式:
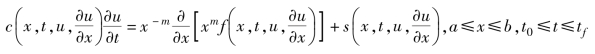
然后对偏微分方程(组)编写下面的入口函数:
![]()
其中,du是u的一阶导数,由给定的输入变量即可表示出c、f、s这三个函数.
@icfun:是偏微分方程(组)的初值条件描述函数,必须先转换为下面的标准形式:
u(x,t0)=u0(x),a≤x≤b
然后编写下面的函数即可.
![]()
@bcfun:是偏微分方程(组)的边界条件描述函数,必须先转换为下面的标准形式:
![]()
边值条件可以通过下面的函数描述为:
![]()
其中,ul和ur分别是左边界xl=a和右边界xr=b处的近似解;pl、ql和pr、qr分别返回xl=a和xr=b时函数p、q的值.
xmesh:给出需要进行数值解的空间节点.
tspan:给出需要进行数值解的时间节点.
options:给出微分方程的部分优化参数.
sol:一个三维数组,sol(i,j,k)给出解u(k)在xmesh(i)和tspan(j)处的值.
例5.34 求解下面的偏微分方程组:
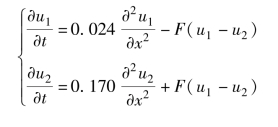
其中,F(y)=e5.73y-e-11.46y,初值条件和边值条件分别为
u1(x,0)≡1,u2(x,0)≡0
和
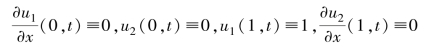
解:首先将给定的微分方程组、初值条件、左边界条件和右边界条件分别转换为如下的标准形式:
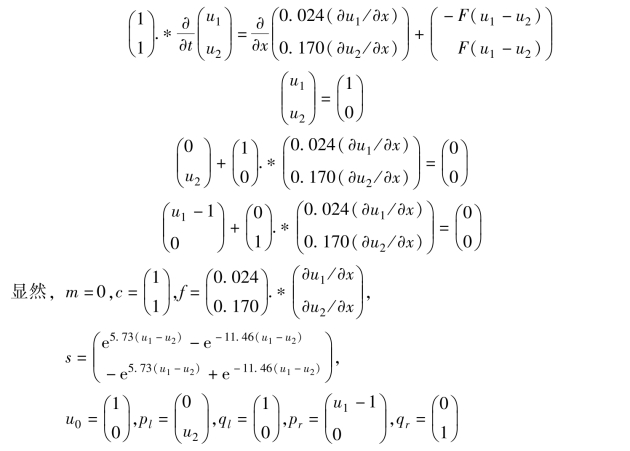
然后编写如下的代码进行MATLAB求解:


运行结果如图5-15所示.
2.特殊偏微分方程的数值解运算
MATLAB提供了专门用于求解二维偏微分方程的工具箱(PDE toolbox).
PDE toolbox提供了GUI可视交互界面pdetool,在pdetool中可以很方便地求解一个PDE问题,并且可以直接生成M代码.
下面给出MATLAB pdetool能够计算的四种特殊的二阶偏微分方程:
(1)椭圆型
-∇⋅(c∇u)+au=f.
(2)抛物型
![]()
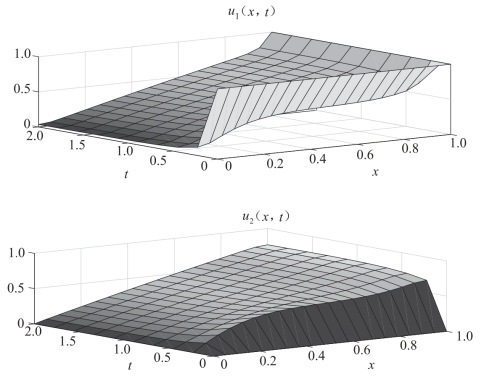
图5-15 一般偏微分方程数值解图像
(3)双曲型
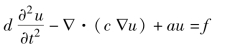
(4)特征值型
-∇⋅(c∇u)+au=λdu
上述所有方程都是在二维平面区域Ω上,方程中∇是梯度算子,u是待解的未知函数,c、a、f和d是已知的方程系数.在椭圆型方程中,这些系数可以是常数或者函数,但在抛物型和双曲型方程中必须为常数,λ是未知的特征值.
在MATLAB pdetool中处理的偏微分方程的边界条件包括Dirichlet条件和Neumann条件:
(1)Dirichlet条件
![]()
其中,∂Ω表示求解域的边界;r和q可以是常数,也可以是给定的函数.
(2)Neumann条件
![]()
其中,![]() 表示u的法向偏导数.
表示u的法向偏导数.
在MATLAB命令窗口中键入“pdetool”,打开“pdetool”窗口,即可使其进入工作状态,如图5-16所示.工具栏中的图形按钮功能如图5-17所示.下面以例题形式给出应用pdetool求解偏微分方程数值解的一般过程.
图5-16 pdetool工作界面
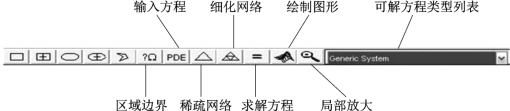
图5-17 pdetool工具栏介绍
例5.35 求解下面的双曲型偏微分方程:
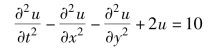
求解区域为Ω=(Ω1∪Ω2)-(Ω1∩Ω2),其中Ω1:x2+y2≤9,Ω2: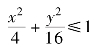
![]() .(https://www.daowen.com)
.(https://www.daowen.com)
解:应用pdetool求解该问题过程如下.
(1)绘制求解区域
pdetool工具栏的前五个按钮,边界条件为![]() 可以分别绘制矩形、椭圆形和多边形区域.其中带“+”号表示区域从图形中心开始绘制.选中相应按钮后,按住鼠标左键即可在适当位置绘制相应图形,而按住鼠标右键可分别绘制正方形和圆.pdetool自动分配给每个图形一个编号,通过双击相应图形可以在弹出的对话框中修改图形参数和名称.另外,可以在工具栏下方的公式设置框中通过图形的名称设置组合图形.
可以分别绘制矩形、椭圆形和多边形区域.其中带“+”号表示区域从图形中心开始绘制.选中相应按钮后,按住鼠标左键即可在适当位置绘制相应图形,而按住鼠标右键可分别绘制正方形和圆.pdetool自动分配给每个图形一个编号,通过双击相应图形可以在弹出的对话框中修改图形参数和名称.另外,可以在工具栏下方的公式设置框中通过图形的名称设置组合图形.
在本题中,首先绘制圆C1和椭圆E1,并修改其参数,使之符合题目中Ω1和Ω2的要求.然后通过在公式框中输入“(C1-E1)+(E1-C1)”,即可得到本题求解区域Ω,如图5-18所示.
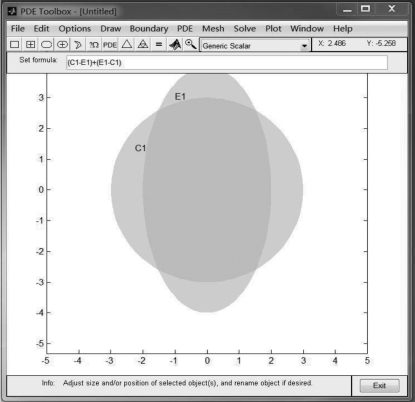
图5-18 求解区域
(2)输入边界条件
首先,单击工具栏第六个按钮![]() ,生成求解区域的边界曲线.然后通过“Boundary”菜单下的“Remove All Subdomain Borders”命令移除所有子区域的边界,得到所有子区域合并后的求解区域.最后,选中相应边界后(选中的边界为黑色,Dirichlet边界为红色,Neumann边界为蓝色),双击该边界,在弹出的边界条件对话框中输入该边界标准形式下的系数即可.本题中,所有边界均为Dirichlet边界,系数h=1,r=5,生成的边界如图5-19所示.
,生成求解区域的边界曲线.然后通过“Boundary”菜单下的“Remove All Subdomain Borders”命令移除所有子区域的边界,得到所有子区域合并后的求解区域.最后,选中相应边界后(选中的边界为黑色,Dirichlet边界为红色,Neumann边界为蓝色),双击该边界,在弹出的边界条件对话框中输入该边界标准形式下的系数即可.本题中,所有边界均为Dirichlet边界,系数h=1,r=5,生成的边界如图5-19所示.
(3)输入微分方程
单击工具栏第七个按钮![]() ,在弹出的对话框中选择相应的偏微分方程类型,并按照其标准形式输入方程的系数.本题中,偏微分方程为双曲型,系数分别为d=1、c=1、a=2和f=10.
,在弹出的对话框中选择相应的偏微分方程类型,并按照其标准形式输入方程的系数.本题中,偏微分方程为双曲型,系数分别为d=1、c=1、a=2和f=10.
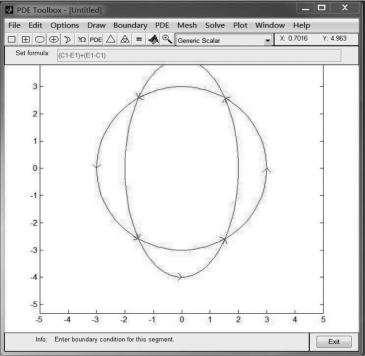
图5-19 求解区域边界
(4)划分有限元网格
单击工具栏的第8个和第9个按钮![]() ,可以对求解区域进行三角剖分.多次单击精细网格按钮,可以在原来基础上多次细化网格.另外,可以通过“Mesh”菜单对网格进行精确控制.本题中,网格剖分后如图5-20所示.
,可以对求解区域进行三角剖分.多次单击精细网格按钮,可以在原来基础上多次细化网格.另外,可以通过“Mesh”菜单对网格进行精确控制.本题中,网格剖分后如图5-20所示.
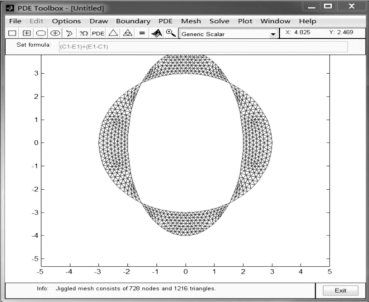
图5-20 求解区域网格剖分
(5)求解微分方程
单击工具栏的第10个按钮![]() ,求解微分方程.
,求解微分方程.
(6)可视化数值解
单击工具栏的第11个按钮![]() ,在弹出的对话框中可以设置绘制微分方程数值解图形的各种参数.本题求解结果如图5-21所示.
,在弹出的对话框中可以设置绘制微分方程数值解图形的各种参数.本题求解结果如图5-21所示.
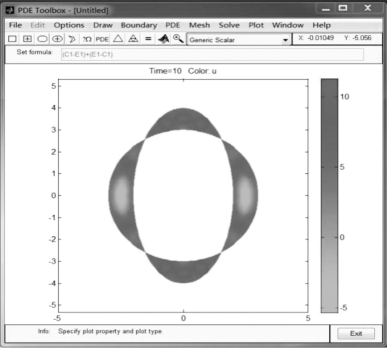
图5-21 数值解图形
第5章练习题
1.求下列极限.
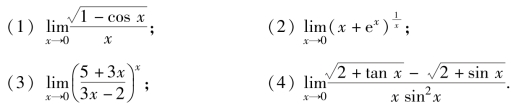
2.确定下列函数的间断点并判断其类型.

3.求下列函数的导数.
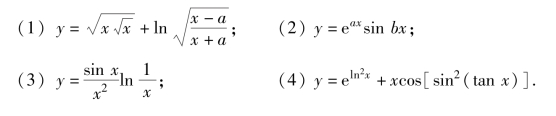
4.在曲线y=1-x2(x>0)上求一点P的坐标,使曲线在该点处的切线与两坐标轴所围的三角形的面积最小.
5.求下列定积分.
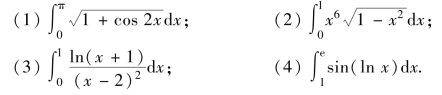
6.求下列二重积分.
(1)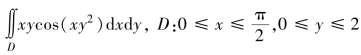 ;
;
(2)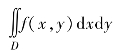 ,其中
,其中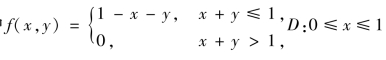 ,0≤y≤1;
,0≤y≤1;
(3)![]() ;
;
(4)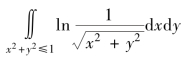 .
.
7.求下列三重积分.
(1)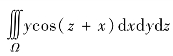 ,Ω:由
,Ω:由![]() 围成;
围成;
(2)![]() ,Ω:由x2+y2-z2=0,z=1围成;
,Ω:由x2+y2-z2=0,z=1围成;
(3)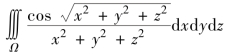 ,Ω:π2≤x2+y2+z2≤4π2;
,Ω:π2≤x2+y2+z2≤4π2;
(4)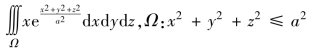 在第一卦限的部分.
在第一卦限的部分.
8.求下列曲线积分.
(1)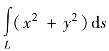 ,L为曲线x=a(cos t+t sin t),y=a(sin t-tcos t),0≤t≤2π;
,L为曲线x=a(cos t+t sin t),y=a(sin t-tcos t),0≤t≤2π;
(2)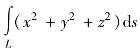 ,L为螺线x=acos t,y=asin t,z=bt,0≤t≤2π;
,L为螺线x=acos t,y=asin t,z=bt,0≤t≤2π;
(3)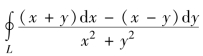 ,L为圆周x2+y2=4(按逆时针方向绕行);
,L为圆周x2+y2=4(按逆时针方向绕行);
(4)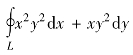 ,L为直线x=1与抛物线x=y2所围区域边界(按逆时针方向绕行).
,L为直线x=1与抛物线x=y2所围区域边界(按逆时针方向绕行).
9.求下列曲面积分.
(1)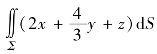 ,Σ为平面
,Σ为平面![]() 在第一卦限的部分;
在第一卦限的部分;
(2)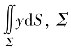 为上半球面
为上半球面![]() ;
;
(3)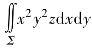 ,Σ为球面x2+y2+z2=a2的下半部分的下侧;
,Σ为球面x2+y2+z2=a2的下半部分的下侧;
(4)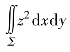 ,Σ为平面x+y+z=1在第一卦限部分的上侧.
,Σ为平面x+y+z=1在第一卦限部分的上侧.
10.判别下列级数的敛散性.
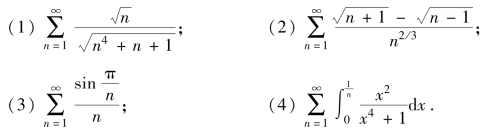
11.求下列幂级数的收敛半径与收敛域
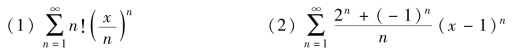
12.将函数f(x)=x2,x∈[0,2π]展开成傅里叶级数.
13.求解下面的微分方程组:
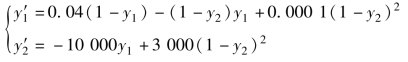
其中,y2(0)=y1(0)=1,t∈[0,100].
14.求解下列热传导定解问题:
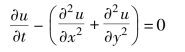
其中满足: