5.3.2 幂级数与傅里叶级数
一、幂级数
给定一个定义在区间I上的函数列un（x）（n＝1，2，3，…），称
为一个函数项级数.
形如
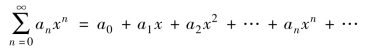
的函数项级数称为幂级数，常数a0，a1，a2，…，an，…称为幂级数的系数.
如果
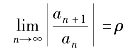
令
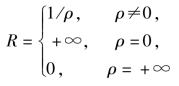
则
时，幂级数绝对收敛；
当
当
时，幂级数发散；
当x＝R与x＝-R时，幂级数可能收敛也可能发散.
R称为幂级数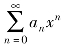
的收敛半径.
例5.27 求下列幂级数的收敛半径.
(1)
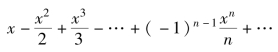
(2)
(3)1＋x＋2!x2＋3!x3＋…＋n!xn＋…
解：
如果函数f（x）在点x0的某邻域内能展开成如下幂级数
f(x)＝a0＋a1(x-x0)＋a2(x-x0)2＋…＋an(x-x0)n＋…
则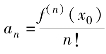
，即
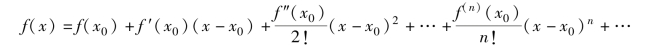
上述幂级数称为函数f（x）在点x0的处的泰勒级数.特别地，当x0＝0时，该级数称为函数f（x）的Maclaurin级数.
MATLAB提供了函数taylor来求解函数的泰勒展开式，其调用格式为
其中，f是待展开函数的符号表达式；v是函数的符号变量；Name和Value用来给出参数选项，如，‘ExpansionPoint’可以给出泰勒展开的位置（默认为0），‘Order’可以给出泰勒展开的项数（默认为6）.
例5.28 求函数f（x）＝ex在点x＝1处的1～3阶泰勒展开式.
解：首先计算f（x）的1～3阶泰勒展开式：
下面绘制f（x）及其1～3阶泰勒展开式的图形：
运行结果如图5-9所示.
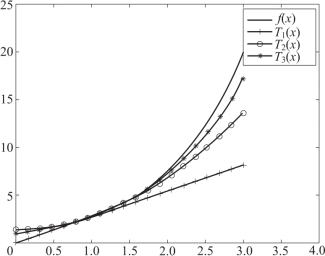
图5-9 函数及其泰勒展开式图形
二、傅里叶级数
设f（x）是以2l为周期的周期函数，如果积分
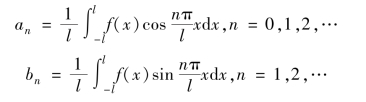
都存在，则称三角级数
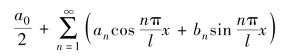
为函数f（x）的傅里叶级数.
MATLAB目前没有提供专门的求解函数的傅里叶级数的命令，但是通过上述公式可以通过调用int函数编写如下的求解函数的傅里叶级数的函数文件，代码如下：
注意：也可以通过调用数值积分函数quad来求解函数的傅里叶级数，此时得到的不再是傅里叶级数的展开式，而是傅里叶级数在指定点上的值，这里不再赘述.
例5.29 分别用1、10和20阶傅里叶级数对[-1，1]上的方波信号
进行拟合.
解：首先，通过调用fourierseries函数可以分别计算f（x）的1阶、10阶和20阶傅里叶级数展开式F1（x）、F10（x）、F20（x），执行如下语句：
然后绘制f（x）及F1（x）、F10（x）、F20（x）的图形：
运行结果如图5-10所示.
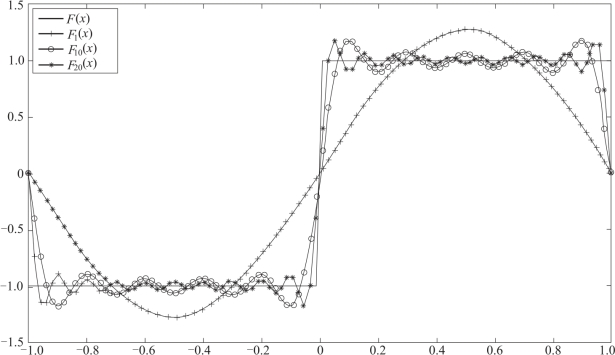
图5-10 方波及其傅里叶级数拟合