5.1.1　函数极限与间断点的计算

5.1.1　函数极限与间断点的计算

一、函数的极限

当自变量x趋于有限数x0时，函数f（x）的极限及其左极限和右极限的定义可以分别表述为

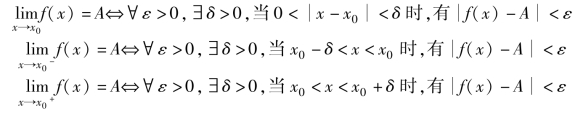
当自变量x趋于无穷大时，函数f（x）的极限的定义可以表述为

对于二元函数f（x，y），当自变量（x，y）趋于（x0，y0）时，函数f（x，y）的极限的定义可以表述为

时，有

若二重极限存在，则两个二次极限和也存在，且三者相等.

在MATLAB中，提供了limit函数来求解函数的极限，其调用格式为

其中，L是返回的极限值；expr为极限的符号表达式；x为符号自变量（expr只含一个符号变量时可省略）；x0为极限点（默认值为0），可以是确定的数、符号表达式或无穷大；‘left’和‘right’分别为左、右单侧极限选项.

例5.1　求下列函数极限：

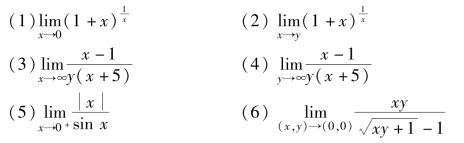
解：

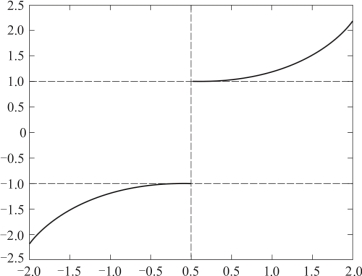
此外，也可以借助MATLAB强大的绘图功能，通过函数的图形来直观地观察函数的极限.以为例，编写如下语句实现在图形上直观地观察出函数极限：

运行结果如图5-1所示.

图5-1　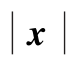/sin x及其在0点的左、右极限

二、函数的间断点

如果函数f（x）在点x0处满足下列3种情形之一：

①在x＝x0处没有定义；

②不存在；

③存在，但.

则称函数f（x）在点x0处不连续，而点x0称为f（x）的间断点.

间断点一般可以分为：

①第一类间断点，又可以分为

（i）可去间断点：；

（ii）跳跃间断点：和都存在，但.

②第二类间断点，不是第一类间断点的任何间断点都称为第二类间断点.

可以编写程序用来判断点x0是否是函数f（x）的间断点，并给出间断点类型，程序如下：

通过调用上述函数文件即可判定函数的间断点类型.

例5.2　判定下列函数间断点的类型.

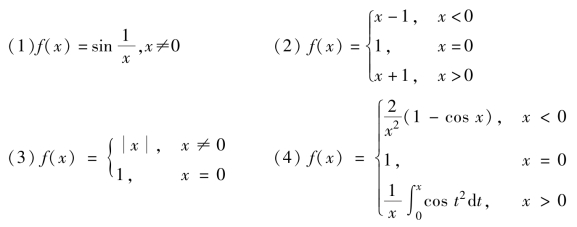
解：