7.1.2 关键参数蒙特卡洛估计的MATLAB实现
2026年01月14日
7.1.2 关键参数蒙特卡洛估计的MATLAB实现
研究数据来自中国卫生部网站公布的2009年6月14日—7月11日的甲型H1N1流感疫情数据,见表7-1.
表7-1 疫情数据
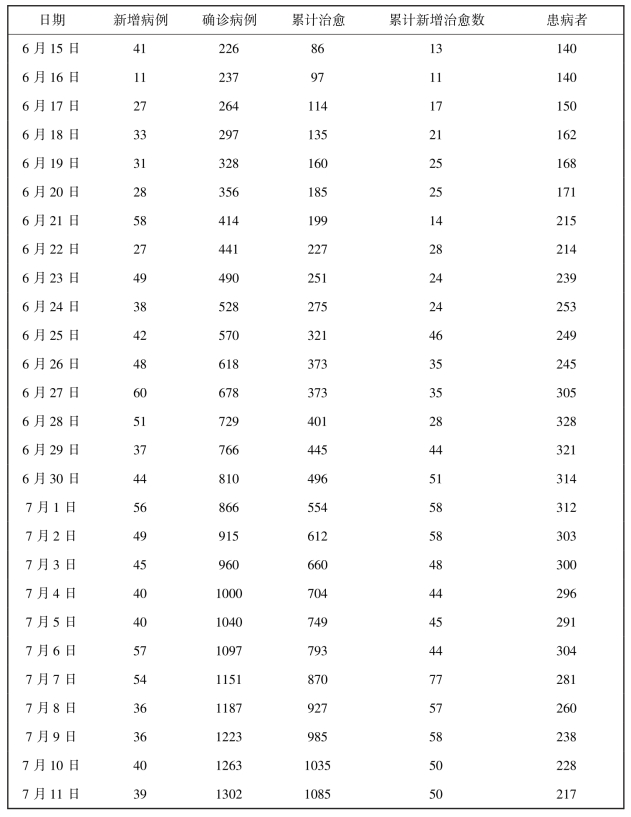
四类人群的初值见表7-2。
表7-2 四类人群的初值

据统计,2009年全国自然出生率为12.13‰,自然死亡率为7.08‰,甲流的病死率是0.54%.假定总人口恒定,计算可得A=116人.甲流患者一般需要1周左右的时间痊愈,甲流的潜伏期为1~7天,本章取中位数4天作为甲流潜伏期.部分参数值见表7-3.
表7-3 部分参数值

利用表7-1的数据、表7-2的初值及表7-3的参数值,通过非线性最小二乘法估计出参数β值为1.194×10-7,拟合曲线如图7-3所示.MATLAB程序如下:

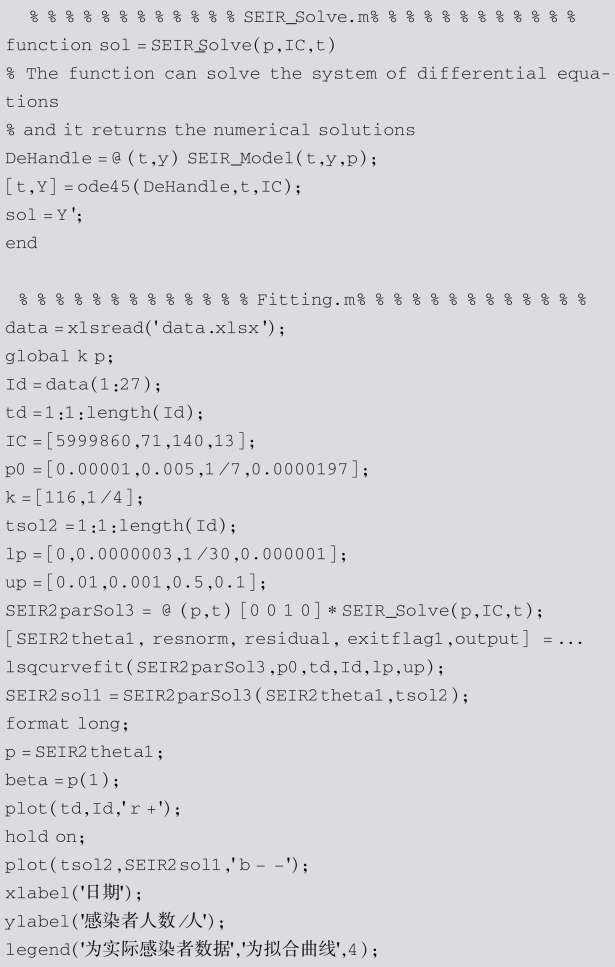

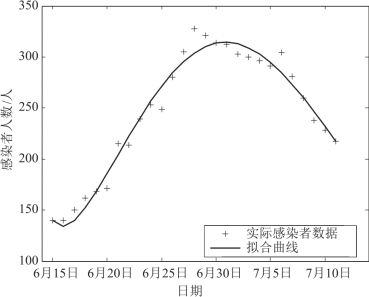
图7-3 参数拟合曲线(https://www.daowen.com)
基于上面的结果,用Bootstrap蒙特卡洛方法对β进行区间估计,具体步骤如下.
①定义残差:
![]()
从而有
![]()
②通过从{ε1,ε2,…,εn}中均匀随机抽样,产生一个Bootstrap样本![]() ,同时用最小二乘法估计β值,得到
,同时用最小二乘法估计β值,得到![]() .
.
③重复过程②N次,得到![]() .
.
④用百分位法来确定置信区间.对![]() 按从小到大进行排序,得到
按从小到大进行排序,得到![]() .令β的置信水平为1-α,取
.令β的置信水平为1-α,取![]() ,
,![]() ],以
],以![]() 分别作为
分别作为![]() 的估计,从而得到β的置信水平为1-α的近似置信区间为
的估计,从而得到β的置信水平为1-α的近似置信区间为![]() .
.
⑤通过MATLAB编程实现上述过程,程序如下.
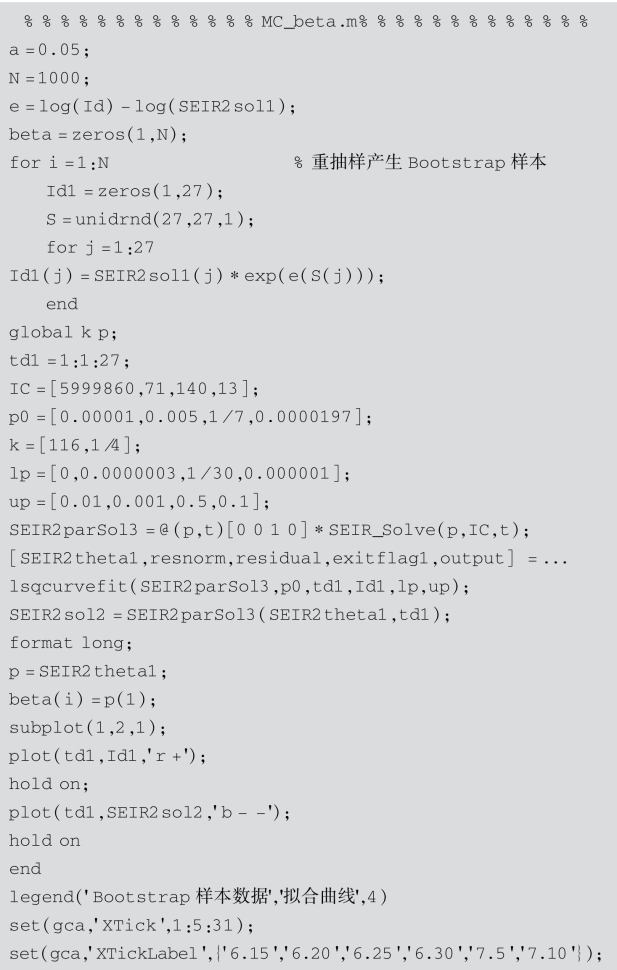
当抽样执行1 000次,即N=1 000时,得到β的95%置信度的置信区间为[1.013 5×10-7,1.430 5×10-7].图7-4(a)为Bootstrap样本和拟合的数据图像,对每个Bootstrap样本运用非线性最小二乘法产生的β的频率分布直方图如图7-4(b)所示.
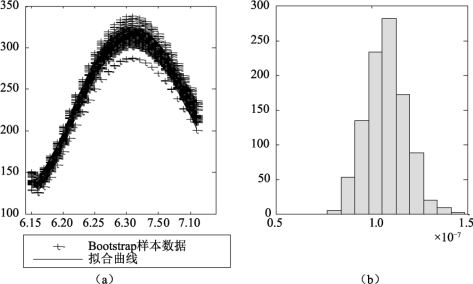
图7-4 Bootstrap方法估计β的置信区间
