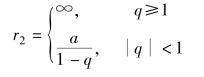5.3.1 常数项级数的收敛性判别与级数求和
一、常数项级数的收敛性判别
一般地,如果给定一个数列
u1,u2,u3,…,un,…
则由这个数列构成的表达式
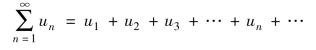
称为常数项级数.其中,第n项un叫作级数的一般项;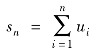 ,称为级数的部分和.
,称为级数的部分和.
如果级数![]() 的部分和数列{sn}有极限s,即
的部分和数列{sn}有极限s,即![]() ,则称无穷级数
,则称无穷级数![]() 收敛,这时s叫作级数的和,并记为
收敛,这时s叫作级数的和,并记为
s=u1+u2+u3+…+un+…
如果{sn}极限不存在,则称无穷级数![]() 发散.
发散.
(1)正项级数比较判别法
设![]() 和
和![]() 都是正项级数,如果
都是正项级数,如果
①![]() ,且级数
,且级数![]() 收敛,则级数
收敛,则级数![]() 也收敛;
也收敛;
②![]() ,且级数
,且级数![]() 发散,则级数
发散,则级数![]() 也发散.
也发散.
例5.20 判定级数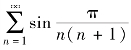 的敛散性.
的敛散性.
解:利用比较判别法,与级数![]() 进行比较得
进行比较得
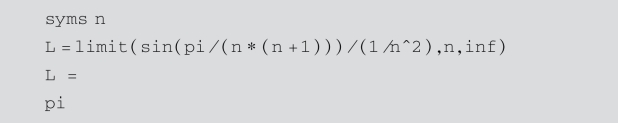
由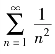 收敛知,原级数收敛.
收敛知,原级数收敛.
(2)正项级数比值判别法
设![]() 是正项级数,如果
是正项级数,如果
①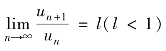 ,则级数
,则级数![]() 收敛;
收敛;
②![]() ,则级数
,则级数![]() 发散;
发散;
③![]() ,则级数
,则级数![]() 可能收敛也可能发散.
可能收敛也可能发散.
例5.21 判定级数![]() 的敛散性.
的敛散性.
解:利用比值判别法,由

可知级数收敛.
(3)正项级数根值判别法
设![]() 是正项级数,如果
是正项级数,如果
①![]() ,则级数
,则级数![]() 收敛;
收敛;
②![]() ,则级数
,则级数![]() 发散;
发散;
③![]() ,则级数
,则级数![]() 可能收敛也可能发散.
可能收敛也可能发散.
例5.22 判定级数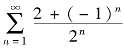 的敛散性.
的敛散性.
解:利用根值判别法,由

可知级数收敛.
(4)交错级数判别法(莱布尼茨定理)
如果交错级数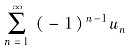 (不妨设u1,u2,…,un,…都是正数)满足条件
(不妨设u1,u2,…,un,…都是正数)满足条件
①un≥un+1(n=1,2,3,…);(https://www.daowen.com)
②![]() ,
,
则级数收敛.
例5.23 判定级数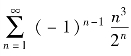 的敛散性.
的敛散性.
解:首先绘制正项级数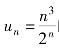 的图像:
的图像:

运行结果如图5-8所示.
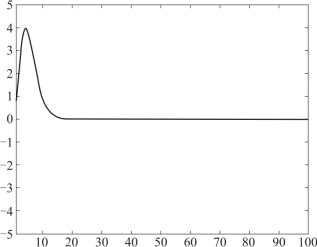
图5-8 级数单调性示意图
可以看出,un在n>10以后单调递减,再计算un的极限:

由莱布尼茨定理知,原级数收敛.
(5)阿贝尔判别法
如果级数![]() 满足条件:
满足条件:
①数列{an}单调有界;
②级数![]() 收敛,则级数收敛.
收敛,则级数收敛.
例5.24 判定级数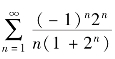 的敛散性.
的敛散性.
解:令![]() ,由
,由

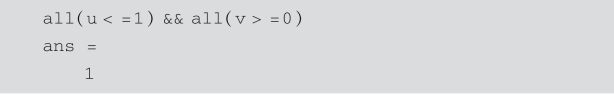
知,an单调递增且有上界1,而由莱布尼茨定理知![]() 收敛,故由阿贝尔判别法知,原级数收敛.
收敛,故由阿贝尔判别法知,原级数收敛.
(6)狄利克雷判别法
如果级数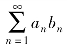 满足条件:
满足条件:
①数列{an}单调趋于零;
②级数![]() 的部分和Bn有界,则级数收敛.
的部分和Bn有界,则级数收敛.
例5.25 判定级数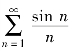 的敛散性.
的敛散性.
解:令![]() ,由
,由

知bn的部分和有界,而an显然单调趋于0,由狄利克雷判别法知,原级数收敛.
二、级数求和
![]()
MATLAB符号运算工具箱提供了函数symsum来求解数项级数的和,该函数的调用格式为其中,expr是级数一般项的字符表达式;v是级数的自变量;a和b分别是级数求和的起始项和终止项;r是返回的级数和.
例5.26 求下列数项级数的和.

解:

注意:piecewise([1<=q,a∗Inf],[abs(q)<1,-a/(q-1)])是MATLAB中定义的分段函数,其数学表达式为