4.4.2 线性方程组的MATLAB求解
求解线性方程组有多种方法，在MATLAB中可以通过高斯消元法、矩阵除法、矩阵求逆等方法求解.
1.高斯消元法
求解线性方程组可以通过高斯消元法，即将增广矩阵[A b]通过行方向的线性运算变形为[D nb]形式，其中D是A的标准形，即和A大小相同且其最左上部分是一个单位矩阵，其他元素都为0.
①对于恰定方程组，D是和A同尺寸的单位矩阵，此时方程组的解的每一个分量可以通过X（i）＝nb（i）/D（i，i）计算得到.
②对于欠定方程组，D的左上部是一个比A小的k×k的单位矩阵，这时候把i>k的X（i）置为0，i≤k的X（i）就可以通过X（i）＝nb（i）/D（i，i）计算得到（一个特解）.
③对于超定方程组，高斯消元后只能看出该方程组没有解.
MATLAB中可以通过rref（[A b]），得到线性方程组扩展矩阵[A b]的高斯消元后的[D nb]矩阵，由此矩阵形式就可以直接计算出线性方程组的一般解.
例4.16 用高斯消元法求解线性方程组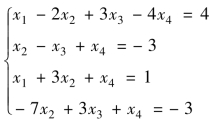
.
解：在命令窗口输入：
由D为单位阵，可知方程组为恰定方程组，且唯一解为[-8，3，6，0]′.
对于有无穷多个解的欠定方程组，要获得其一般解的形式，可以先求齐次线性方程组A∗X＝0的通解ξ＝c1ξ1＋…＋cn-rξn-r（其中，ξ1，…，ξn-r为一个基础解系，c1，…，cn-r为任意常数），再求非齐次线性方程组A∗X＝b的一个特解r0，那么A∗X＝b的一般解就可以表示为ξ＋r0.MATLAB中求解A∗X＝0，可以用null命令，null（A）返回A∗X＝0的解空间的一组标准正交基.
例4.17 用高斯消元法求解欠定方程组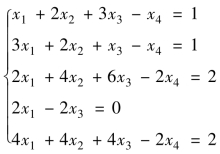
.
解：在命令窗口输入：
即基础解系
ξ1＝[-0.4314，0.7705，-0.4314，-0.1874]′；
ξ2＝[-0.0786，-0.3141，-0.0786，-0.9428]′
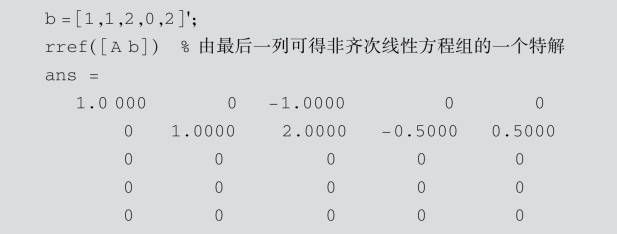
通过得到的高斯消元结果，可以看到此方程组至少有一个特解r0＝[0，0.5，0，0，0]′.
因此，欠定方程组A∗X＝b的一般解可以表示为：
对于超定方程组，高斯消元结果只能看出该方程组没有一般意义的解.通常，各种数学软件都会在最小二乘意义上给出超定方程组的解，即min‖A∗X-b‖.MATLAB中也是如此.
2.矩阵除法求解
求解线性方程组最简单的办法是用矩阵的除法.A∗X＝b的解可以由X＝A＼b得到，X∗A＝b的解可以由X＝b/A得到，注意，这里应用左除和右除对应的方程组形式的不同.
矩阵除法求解线性方程组，不会返回方程组类型的信息，即无论哪种类型的方程组，MATLAB矩阵除法都会返回一个计算结果.对于恰定方程组，这个结果就是其唯一解；对于欠定方程组，此结果是其一个特解；对于超定方程组，计算结果是方程组最小二乘意义上的解.
例4.18 用矩阵除法求解线性方程组.
解：在命令窗口输入：
A∗X＝b是一个欠定方程组，这从A的形状及rref（[A b]）的结果都可以看到，A＼b返回方程组的一个特解，根据rref（[A b]）也只能得到方程组的一个特解（可以不是同一个特解）；当B∗X＝c是一个超定方程组时，通过B＼c求得的解x就是最小二乘意义上方程组的解.因此，B∗X不精确等于c，下例通过绘图可以看出.
例4.19 解超定方程组.
如图4-3所示，圆圈代表B∗X数据点，星号代表c数据点，可以看到有偏差.
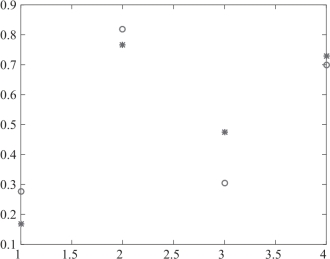
图4-3 超定方程组最小二乘意义下的解
3.矩阵求逆求解
求解线性方程组也可以通过逆矩阵的方法.对于方程组A∗X＝b.
①当A是方阵时，X＝inv（A）∗b；
②当A不是方阵时，X＝pinv（A）∗b.
这样求解得到的线性方程组的解和高斯消元法、矩阵除法得到的结果应该是一致的.
MATLAB求解线性方程组，效率最高的是矩阵除法，因为除法会自动识别系数矩阵A的特征而采用针对性的高效算法，因此，建议尽量多用矩阵除法求解线性方程组.
4.利用矩阵分解求解线性方程组
矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积.常见的矩阵分解有LU分解、QR分解、Cholesky分解、Schur分解、Hessenberg分解及奇异值（SVD）分解等.通过矩阵分解方法求解线性方程组的优点是运算速度快，可以节省存储空间.