4.6.1 线性规划
线性规划(linear programming,LP)就是对满足有限多个线性的等式或不等式约束条件的决策变量的一个线性目标函数求最大值或最小值的最优化问题.线性规划模型的一般表达式可写成
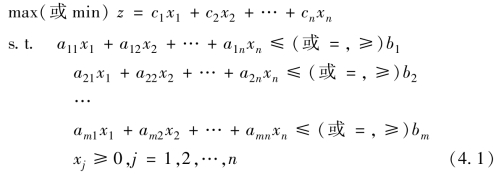
引入记号A=(aij)m×n,x=(xi)n×1,c=(ci)n×1,b=(bi)m×1,则线性规划问题可改写为:
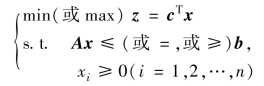
式中,x称为决策变量;z为目标函数.目标函数的变量系数c称为费用系数,约束条件的变量系数A称为约束矩阵或工艺系数,约束条件右端的常数b称为右端向量或资源限量.约束条件前的记号“s.t.”是“subject to”的缩写,意即“受约束于”.决策变量的上下界约束是线性规划模型的一类特殊的线性不等式约束条件,在实践中,一般xj≥0(即非负约束),但有时xj≤0或xj无符号限制.在理论上和计算上,决策变量的上下界约束一般要单列.
MATLAB优化工具箱函数linprog用于求解以下形式的线性规划模型:
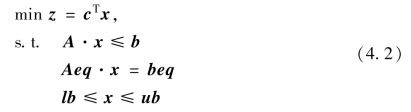
其中,A和Aeq是矩阵;x、c、b、beq、lb和ub是列向量(但MATLAB允许用行向量).
一般的线性规划问题很容易转化为形如式(4.2)的线性规划问题:
①目标函数乘以-1,可使最大值问题转化成最小值问题,最优解相同,最优值互为相反数.
②大于或等于类型的约束乘以-1,就转换成小于或等于类型约束.
函数linprog的语法格式:
(1)x=linprog(c,A,b,Aeq,beq,lb,ub)
输入项c、A、b、Aeq、beq、lb和ub分别是式(4.2)当中的向量或矩阵;输出项x是最优解.如果某个xi无下界或者无上界,可设定lb(i)=-inf或ub(i)=inf.
(2)[x,z,exitflag]=linprog(c,A,b,Aeq,beq,lb,ub,x0)
输出项z是x处的最优值,x0表示初始点,第三输出项exitflag,返回一个整数,描述linprog结束的原因:
1 目标函数在x收敛;
0 迭代次数超出options.MaxIter;
-2 问题没有可行解;
-3 问题的可行域是无界的,没有最小值;
-4 在算法执行过程中遭遇特殊值NaN;
-5 原问题和对偶问题都是不可行的;(https://www.daowen.com)
-7 搜索方向太小,不能计算下去.
(3)[x,z,exitflag,output]=linprog(c,A,b,Aeq,beq,lb,ub,x0,options)
第四输出项output返回一个包含优化信息的结构数组,输入项options表示优化参数,可选择3种算法之一:interior-point、active-set、simplex.options.缺省时默认算法interior-point,其他算法选择可通过optimset或optimoptions完成,如:

(4)[x,z,exitflag,output,lambda]=linprog(c,A,b,Aeq,beq,lb,ub)
第五输出项lambda是一个结构数组,包含在最优解处的不同约束类型的拉格朗日乘子(即影子价格)的信息.lambda具有以下4个域:
lower 决策变量的下界限制lb对应的拉格朗日乘子列向量;
upper 决策变量的上界限制ub对应的拉格朗日乘子列向量;
ineqlin 不等式约束对应的拉格朗日乘子列向量;
eqlin 等式约束对应的拉格朗日乘子列向量.
当某个约束对应的拉格朗日乘子等于0时,就说明该约束是无效约束,也就是该约束在最优解x处不等号严格成立;当某个约束对应的拉格朗日乘子不等于0时,就说明该约束是有效约束,也就是该约束在最优解x处等号严格成立.
无论是输入项还是输出项,从右往左连续缺省的若干项是可以省略的,例如:[x,z]=linprog(c,A,b,Aeq,beq,lb);,输入项的缺省项可以用[]表示.例如,没有等式约束:[x,z]=linprog(c,A,b,[],[],lb);,输出项不能从中间缺省.
例4.22 解线性规划问题.
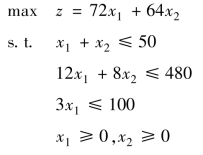
解:

MATLAB还带有优化工具箱(Optimization Toolbox),提供了包括线性规划、非线性规划和遗传算法等多种优化算法的优化工具指令optimtool,在命令窗口直接运行optimtool,将打开如图4-4所示的界面.该界面提供了优化算法选择及相应的参数设置和运算等的可视方式,如要优化的问题和约束条件等可以通过列表框直接填写,单击“Start”按钮即可开始.
下面用优化工具求解例4.22.在命令窗口运行optimtool,参照图4-4.选择填写并运行即可,求解结果与上面相同,命令窗口显示的结果如图4-5所示.
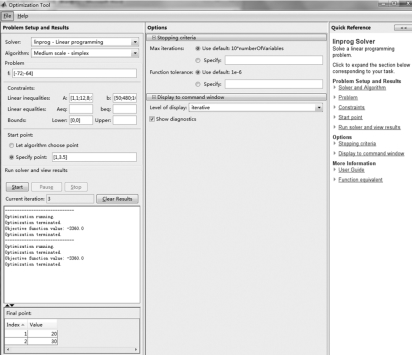
图4-4 使用优化工具箱
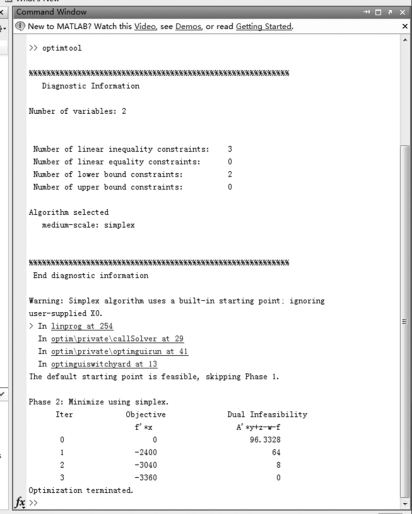
图4-5 优化工具箱使用结果
