7.2.2 血液光谱数据分类识别的MATLAB实现
光谱识别技术中，传统的模式识别方法主要基于特征模式描述的判别函数法（又叫统计模式识别法，Statistical pattern recognition）和基于基元模式描述的句法模式识别法（syntax pattern recognition）.其中，句法模式识别法以图形结构特征为基础，运用形式语言理论的技术，适用于复杂景物图像分析和理解；判别函数法以实验样本在特征空间中的类概率密度为基础.光谱识别技术主要采用的是判别函数法.
对于光谱，常利用光谱线的波长、强度和谱线宽度等特征信息，对光谱进行识别.识别方法一般是采用分类技术，将待识别光谱与已知的模板光谱匹配，从而将待识别光谱划分到相应的类别上.在实际中，由于获取光谱时的测量误差、强噪声的干扰、识别技术的限制，使得待测光谱与模板很难匹配准确，造成光谱识别率较低.
传统的统计模式分类方法是以经典统计学为基础，在假设训练样本数目足够多的前提下进行研究的，只有当训练样本无穷大时，其性能才能达到理论上的最优.然而，在很多实际的模式识别问题中，样本数目是有限的，无法获得各类的先验概率和概率分布密度函数，难以形成复杂的判别函数和分割界面等.人工神经网络分类方法（如BP网络）具有良好的容错能力和自适应性，对模式先验概率分布的要求较小，因而具有比较好的性能，但是神经网络方法也有一些缺点，如局部极值点问题、训练收敛速度太慢、分类性能对各类差别较大等.
模糊模式识别不需要对数据的概率分布做出任何假设，也不需要估计概率密度中的参数，通过对训练样本的直接统计学习，掌握样本中隐含的规律，实现对数据的划分；由于受到噪声、仪器状态、实验员人为原因等诸多因素的影响，光谱的高度重复性不强，大量数据和研究表明，很难对其进行精确分类，模糊模式识别方法是利用模糊数学的原理与方法解决分类识别的问题，以获得含有更多信息、更真实的结果.
模糊模式识别方法通过建立隶属函数，用模糊集合来标记问题论域中客观存在的不确定性，并基于模糊集理论中简便有效的集合运算来实现特征量的操作和变换，因而能够模仿人脑判别不确定性事物的机理，充分利用冗余信息，有效处理各种不确定性信息，提高识别系统的可靠性和智能程度.
以上述理论为指导，采用了糊模式识别的方法对动物全血发射光谱进行分类识别.待处理的光谱数据为羊、鼠、鸡、鸽全血发射光谱数据，是在长春理工大学激光与纳米材料实验室采集的，光谱仪的参数为：仪器（Cary Eclipse）、仪器序列号（MY13450002）、采样类型（荧光）、扫描模式（发射）、激发波长（200 nm）、激发狭缝（5 nm）、发射狭缝（10 nm）、扫描速度（600.00 nm/min）.
1.数据预处理
在光谱仪上测量到的光谱数据除有用信号外，还包含噪声，其表现为光谱图上的毛刺，具有高频特征，如图7-9所示，不利于特征提取.为消除这些毛刺，常采用数据平滑技术对原始光谱进行处理，其MATLAB程序如下：
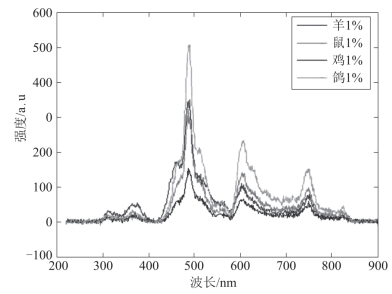
图7-9 原始数据光谱图像
目前，常用的光谱去噪方法主要有FFT（快速傅里叶变换）滤波、小波变换去噪和临域平均值法.采用这些方法并结合MATLAB程序均可以对光谱数据进行平滑处理.经比较，三种方法的平滑结果对血液光谱来说区别不大.考虑到临域平均值法在算法上较为简单，容易实现，因而，采用了临域平均值法对血液光谱数据进行平滑处理.
所谓的临域平均值法，是选取固定的点数，将各点的纵坐标值求和后除以点数，得到这一组数的中心横坐标处的平均纵坐标值.然后，去掉这一组数中左端一个点，向前移动一个采样点，重复上述平均，得到平滑曲线的下一个值.如此反复进行，就可以得到整个曲线平滑后的数据.其数学表达式为：
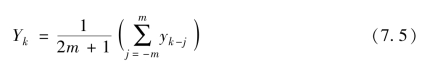
其中，k＝m＋1，m＋2，…，n-m；2m＋1为平滑窗口宽度，即2m＋1点移动平均.
例如，当m＝1时，为三点移动平均
这里，yk-j为不同点的数据值；Yk为以k点为中心的2m＋1个数的平均值.对于光谱平滑处理，光谱两端的数据没有可用信息，对平滑结果也没有影响，故可不做端点处理.
理想白噪声的平滑处理效果，随m的增大而大大改善.但m增大时，信号波形会受平滑处理的影响而产生偏移.在对光谱进行平滑时，m取值越大，谱线越趋光滑，但谱线的细微特征会被平滑掉，也会造成光谱谱线形状畸变，所以需选择合适的m值.在所选光谱仪参数的条件下，光谱平滑次数越多，光谱平滑效果越好，但当平滑次数增多时，光谱微小差别也会被平滑掉，所以平滑次数也要合适.实验表明，对血液光谱进行五点（即m＝2）一次平滑即可得到较好的平滑效果，如图7-10所示.程序如下：
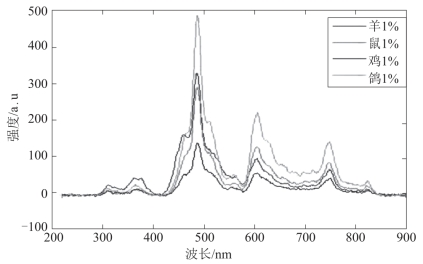
图7-10 平滑处理后光谱图像
因此，在实际处理中，结合MATLAB程序对光谱进行了五点一次平滑.
在MATLAB程序中，常用的平滑方法是smooth函数法，其中smooth函数主要用法如下：
(1)yy＝smooth(y)
用移动平均滤波器对列向量y进行平滑处理，返回与y等长的列向量yy.默认窗宽为5.yy中元素计算方法如下：
yy(1)＝y(1)
yy(2)＝(y(1)＋y(2)＋y(3))/3
yy(3)＝(y(1)＋y(2)＋y(3)＋y(4)＋y(5))/5
yy(4)＝(y(2)＋y(3)＋y(4)＋y(5)＋y(6))/5
yy(5)＝(y(3)＋y(4)＋y(5)＋y(6)＋y(7))/5
(2)yy＝smooth(y，span)
用span参数指定移动平均滤波器的窗宽，span为奇数.
(3)yy＝smooth(y，method)
用method参数指定平滑数据的方法，method是字符串变量.其中参数method可取‘moving’‘lowess’‘sgolay’等.
(4)yy＝smooth(y，span，method)
对于由method参数指定的平滑方法，用span参数指定滤波器的窗宽.
(5)yy＝smooth(y，sgolay，degree)
利用Savitzky-Golay方法平滑数据，此时用degree参数指定多项式模型的阶数.degree是一个整数，取值介于0和span-1之间.
2.特征提取与选择
在模式识别中，特征提取与选择是表示模式对象的关键.在特征空间中，如果同类模式分布比较聚集，不同类模式分布疏远，分类识别就比较容易，正确率较高.在模式识别中，人们希望依据最少的特征达到所要求的分类识别的正确率.这就是特征提取与选择的任务.首先要制定特征提取与选择的准则，以直接反映类内类间距离的函数作为准则，或直接以误判概率最小作为准则，也可以类别判决函数作为准则，还可以构造与误判概率有关的判据来刻画特征对分类识别的贡献或有效性.
常用的特征提取途径有如下两种：
①实际用于分类识别的特征数目d给定后，直接从已获得的n个原始特征中选取d个特征x1，x2，…，xd，使可分性判据J的值满足下式：
其中，xi1，xi2，…，xid是原始特征的任意d个特征，即直接选取n维特征空间中的d维子空间.这类方法被称为直接选择法.
②在使判据J取最大的目标下，对n个原始特征进行降维变换，再取子空间.这类方法称为变换法，主要有基于可分性判据的特征提取选择、基于误判概率的特征提取选择、离散K-L变换法、基于决策界的特征提取选择等方法.
对血液光谱特征的提取与选择，采用了直接选择法.上节中，图7-10为预处理后四类样品血液光谱曲线.谱线在487、605、747 nm附近有明显的波峰，且不同样品的峰值有所不同，故提取此三处附近的波峰进行分析处理.
根据提取的数据，分别计算了四种样品总计200个样本谱线的
（X487、X605、X747表示487、605、747 nm附近的峰位；Y487、Y605、Y747表示487、605、747 nm附近的峰值）.经分析，四种样品光谱曲线在487、605、747 nm附近的波峰有明显的区别，取每类样品三十组，对各特征参数作特征散点图，如图7-11（a）～图7-11（c）所示.程序如下：
观察分析特征图像可知，所取的6个特征参数中，特征
对样品的聚类效果最好，能达到的分类效果最好.所以选取这两个特征进行分类器的设计.
3.分类识别
（1）分类器的设计
这里采用MATLAB程序结合模糊模式识别的方法对血液荧光光谱进行分类识别，选用基于最大隶属度原则设计动物血液光谱分类器.随机选取ni（i＝1，2，…，c）个样本作为训练样本集，c表示样本种类数，并根据所提取的特征，计算每类的聚类中心vi.vi的计算公式如下：
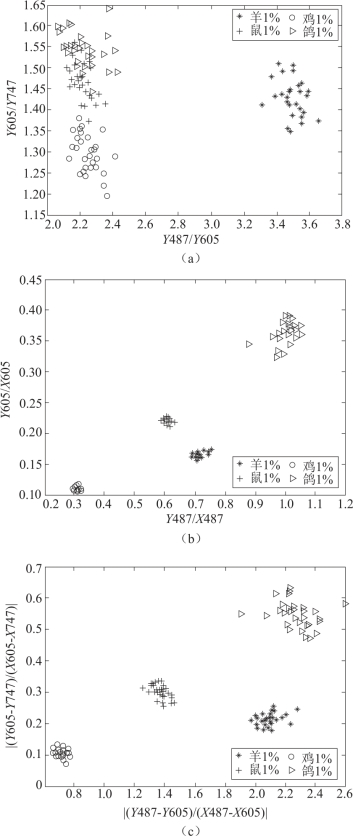
图7-11 不同特征提取结果
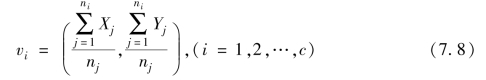
其中，Xj为特征
的值；Yj为特征
的值.
由每个种类样本的聚类中心，即可得到一种分类模式.
（2）分类隶属函数的确立
对于模糊识别技术，分类器的性能主要取决于隶属函数是否优良，因此，建立良好的隶属函数，对识别的效果有决定性的影响.常用的建立隶属函数的方法有专家确定法、统计法、综合加权法等.本节依据待分类样本的特征点到聚类模式中心的距离确定隶属函数.
隶属函数的数学表达式如下：
当d（vi）＝d1或d（vi）＝d2时，
其他
其中，d（vi）为待分类样本特征点到模式vi的欧式距离：
