6.2.1 分布拟合工具箱
在Distribution Fitting Tool中,可以选择例6.1中的数据y1来拟合密度图像,结果如图6-1所示.
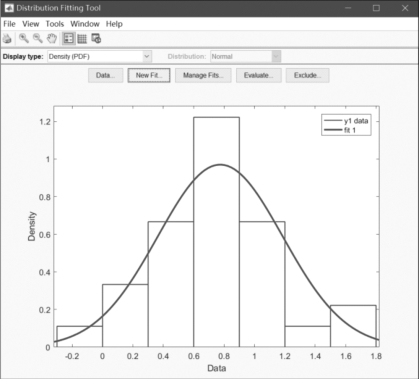
图6-1 在Distribution Fitting Tool中,例6.1中数据y1的拟合密度图
表6-3~表6-7分别列出了概率论与数理统计教材中常见的统计工具箱函数中的概率密度函数、累积分布函数、累积分布函数的逆函数、随机数生成器函数及这些分布的理论统计特性(均值和方差)计算函数.概率密度函数后缀是pdf(Probability Distribution Function)、累积分布函数后缀是cdf(Cumulative Distribution Function)、累积分布函数的逆函数后缀是inv(Inverse Cumulative Distribution Function)、随机数生成器函数后缀是rnd、统计特性计算函数后缀是stat.
对表中的某一分布,如正态分布,就有normpdf、normcdf、norminv、normrnd、normstat五个不同的函数,分别表示正态分布的概率密度函数、累积分布函数、累积分布函数的逆函数,以及其统计特性均值和方差.由于各种分布的解析形式都是已知的,因此这些子程序的编写并不困难.
表6-3 概率密度函数
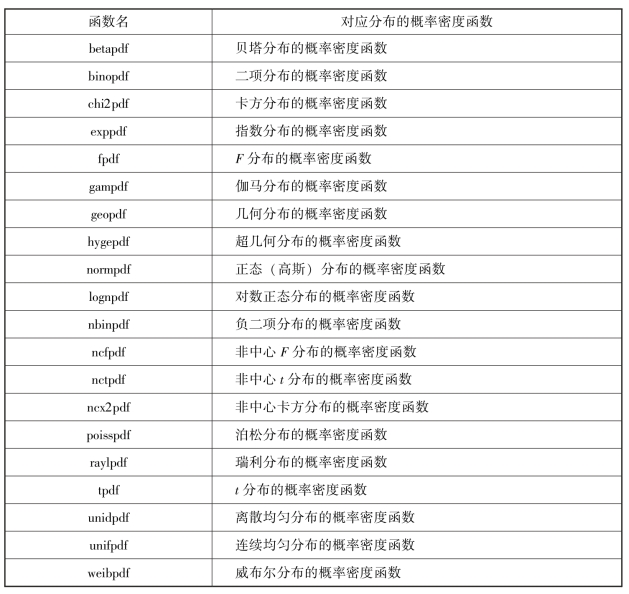
表6-4 累积分布函数

续表
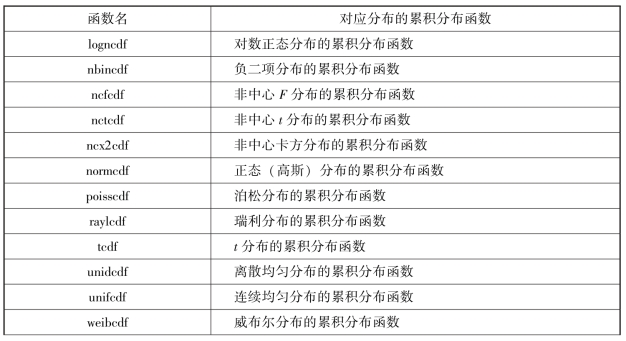
表6-5 累积分布函数的逆函数
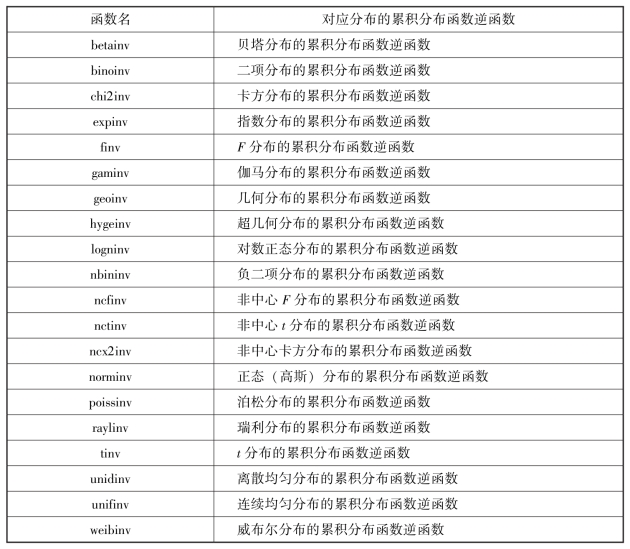
表6-6 随机数生成器函数
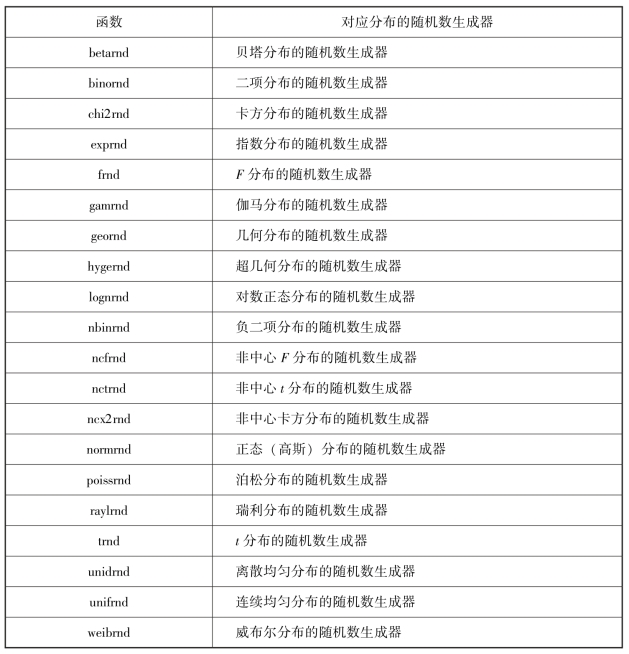
表6-7 分布函数的统计量函数

续表
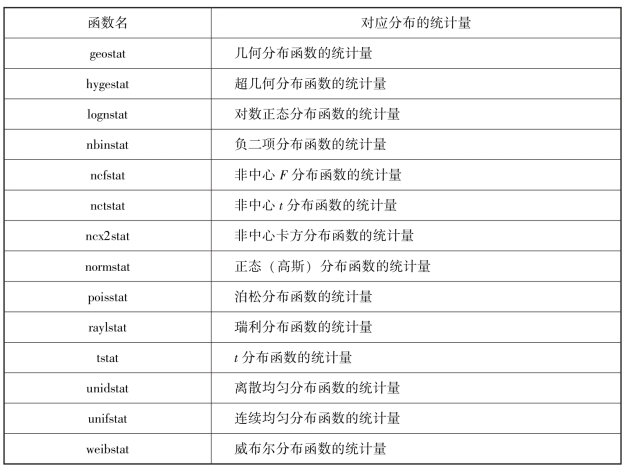
例6.3 利用表中给出的函数,求:
①标准正态分布N(0,1)、自由度为10的卡方分布χ2(10)、二项分布B(10,0.2)的密度函数和分布函数,并画出分布曲线;(https://www.daowen.com)
②求出各分布函数的值分别在0.05和0.95处的各随机变量的值;
③求出各分布的均值和方差.
解:借助于MATLAB中的帮助文件,了解密度函数normpdf、chi2pdf、binopdf和分布函数normcdf、chi2cdf、binocdf的用法,其余雷同.如键入help normcdf,可知

这里,X是一组数据,表示自变量;MU和SIGMA分别为均值和标准差,0和1时可省略.
需要注意的是,一般自变量X的取值不可能取到无穷,因此,一般保证涵盖95%的概率的主要区域即可.如标准正态分布中,X取区间[-3,3]中的数即可.
①程序如下:

运行结果如图6-2所示.需要注意的是,由于二项分布是离散型的,因此概率图像应该画成单点式,而分布函数图像是阶梯形的.
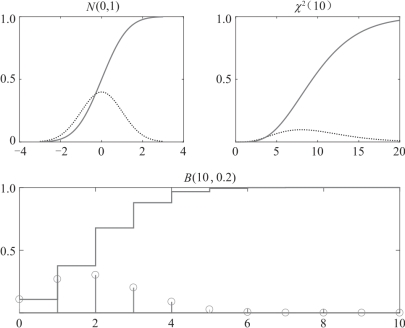
图6-2 运行结果
(a)标准正态分布的概率密度函数和分布函数;(b)卡方分布的概率密度函数和分布函数;(c)二项分布的概率函数和分布函数
②当分布函数F分别为0.05和0.95时,求自变量的值,可用分布函数的逆函数求解.程序如下:

运行结果为:

③程序如下:

运行结果为:

例6.3中给出了正态分布、卡方分布和二项分布三种分布的计算,对其他分布,也可类似进行计算.
