7.1.1 流感传播动力学建模简介
1.传染病动力学理论
传染病动力学是针对传染病的流行规律进行理论性定量研究的一种重要方法,是根据种群生长的特性,疾病的发生及在种群内的传播、发展规律,以及与之有关的社会等因素,建立能反映传染病动力学特性的数学模型.通过对模型动力学性态的定性、定量分析和数值模拟,来分析疾病的发展过程,揭示流行规律,预测变化趋势,分析疾病流行的原因和关键因素,寻求预防和控制的最优策略,为人们制定防治决策提供理论基础和数量依据.近年来,国际上传染病动力学的研究进展迅速,大量的数学模型被用于分析各种各样的传染病问题,也取得了一定的成果.对于2003年发生的SARS疫情,石耀霖构建了SARS传播的系统动力学模型,以越南的数据为参考,进行了Monte Carlo实验.结果表明,感染率及其随时间的变化是影响SARS传播的最重要因素.
从国内外的研究历史和发展现状来看,传染病动力学建模方法最广泛的应用是由Kermack与McK-endrick建立的仓室模型理论.其基本建模思想为:
①将总人口分为易感者(S)、感染者(I)和恢复者(R)等若干类,也称为“仓室”;
②根据各个“仓室”人群流入和流出的平衡关系,建立微分方程模型.
以最简单的SIR模型为例,图7-1的“仓室”图描述的是易感者从染病到康复的过程.建立的微分方程模型为:
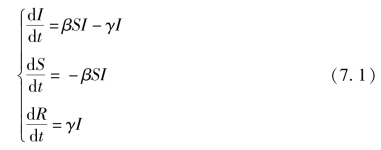
![]()
图7-1 SIR模型“仓室”图(https://www.daowen.com)
其中,β、γ分别表示单位时间内传染病的有效接触率和恢复率.
2.甲型H1N1流感传播模型建立
甲型H1N1流感的传播途径是与病源的直接接触,与普通流感、禽流感相比,潜伏期较长,因此,建立仓室模型时,应考虑加入潜伏者类.对SIR模型加以改进,就可以得到甲型H1N1流感传播的SEIR模型.此时,易感者从患病到康复移出的过程如图7-2所示.
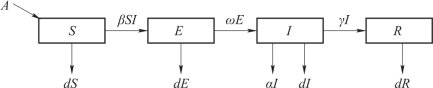
图7-2 SEIR模型“仓室”图
建立的SEIR模型如下:
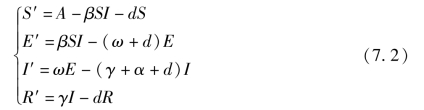
其中,总人口N(t)=S(t)+E(t)+I(t)+R(t);A表示人口的常数输入数目,即单位时间内输入的人口总数,本章认为都是易感者;![]() 为潜伏期;d代表自然死亡率系数;γ表示感染者的恢复率系数;α表示因流感而死亡的死亡率系数.
为潜伏期;d代表自然死亡率系数;γ表示感染者的恢复率系数;α表示因流感而死亡的死亡率系数.
