4.2.6　矩阵的线性空间的标准正交基

4.2.6　矩阵的线性空间的标准正交基

一个矩阵Am×n按列分块（α1，α2，…，αn），则由α1，α2，…，αn生成的线性空间Rm的子空间称为A的线性空间V，即由α1，α2，…，αn的全体线性组合得到的向量组成.

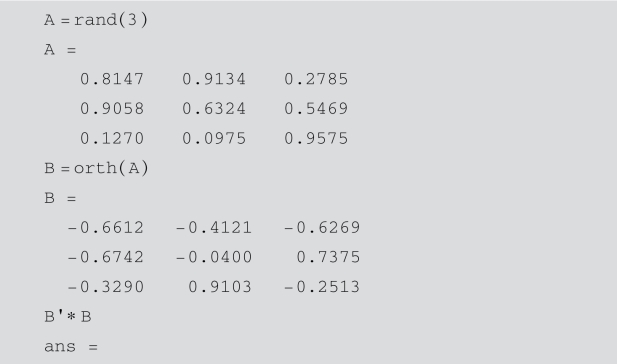
MATLAB中可以通过orth函数产生矩阵A的线性空间的一组标准正交基，即若B＝orth（A），则B的列向量组成了矩阵A的线性空间的一组标准正交基，于是B′∗B＝eye（rank（A））.

例4.4　矩阵的标准正交基.

解：在命令窗口输入：

二次型的标准化，就是对任意的二次型

总有正交变换x＝Py，使之化为标准形，其中

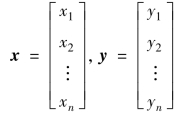
λ1，λ2，…，λn是二次型f的矩阵

(https://www.daowen.com)

的特征值，P为使A对角化的矩阵，即

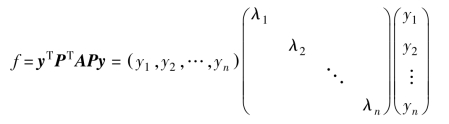
例4.5　求一个正交变换，化下面二次型为标准形：

解：二次型的矩阵为

先求A的特征值和特征向量：

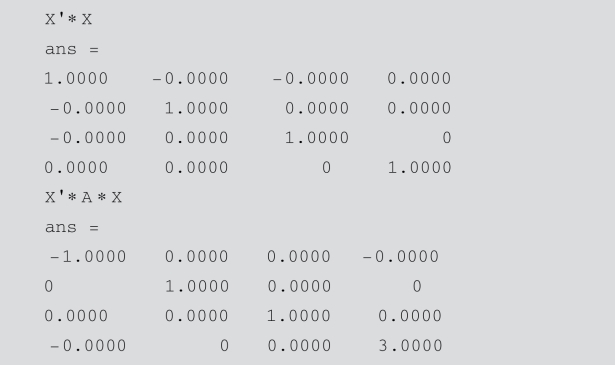
经观察，X的每一列已经正交规范化，所以P＝X，对角矩阵为D，即P′AP＝D.可以验证：