5.1.2 函数导数与极值的计算
一、函数的导数
函数y＝f（x）在点x0处的导数定义为：
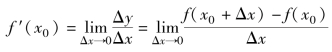
函数u＝f（x，y）在点（x0，y0）处关于x的偏导数定义为：
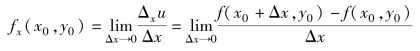
类似地，函数u＝f（x，y）在点（x0，y0）处关于y的偏导数定义为：
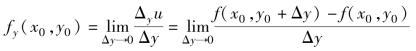
在MATLAB中，提供了函数diff来求解函数的导数，其调用格式为
其中，D是所求的导数；fx是函数的符号表达式；x是符号变量（fx只含一个符号变量时可省略）；n是求导的阶数（默认值为1）.
例5.3 求下列函数的一阶（偏）导数
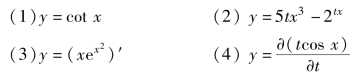
解：
例5.4 作曲线f（x）＝2x3＋3x2-4x＋1的图形和其在x＝-1处的切线.
解：
运行结果如图5-2所示.
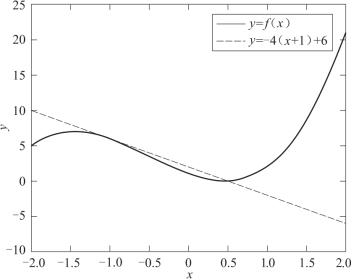
图5-2 函数图形及其切线
二、函数的极值
设函数f（x）在点x0的某邻域U（x0）内有定义，如果对于去心邻域
内的任一x，有
f（x）＜f（x0）（或f（x）>f（x0））
那么就称f（x0）是函数f（x）的一个极大值（或极小值），x0为函数f（x）的一个极大值点（或极小值点）.
例5.5 求函数f（x）＝x3-2x2＋5x-1的极值.
解：步骤如下.
①先用diff函数求f（x）的导函数f′（x）；
②再用solve函数求导函数f′（x）的零点，即函数f（x）的驻点；
③最后用fplot函数绘制f（x）的曲线，判断驻点是否为极值点.
编写如下语句：
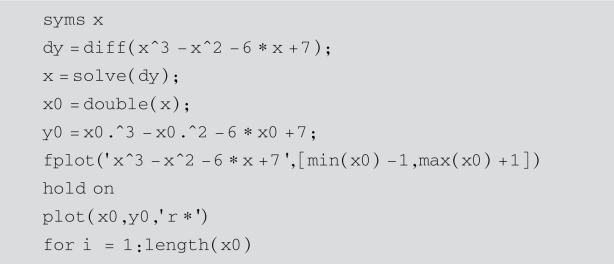
运行结果如图5-3所示.
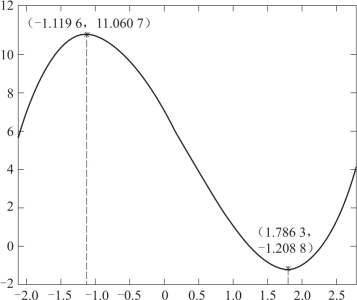
图5-3 函数图形及其极值点坐标
此外，MATLAB优化工具箱中提供了函数fminbnd用于求函数在给定区间上的最小值，其一般调用格式为
这里，fun为函数的符号表达式；x1和x2是区间端点；x是所求得的最小值点；fval是相应的函数最小值；exitflag为结束标志（>0时表示计算结果收敛到最优解x，＝0时表示迭代次数超过允许最大次数，＜0时表示计算结果没有收敛）；output为求解过程的一些信息（迭代次数、算法等）.
例5.6 求函数
在区间[-5，5]上的最大值和最小值.
解：
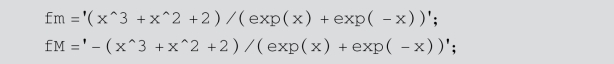
运行结果如图5-4所示.
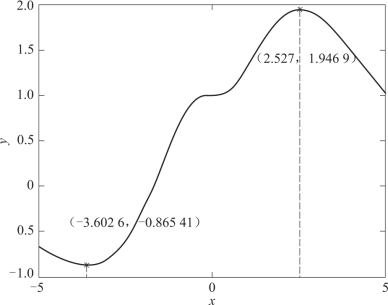
图5-4 函数图形及其最值点坐标