预报模型的建立

一、预报模型的建立

（一）方法概述

对区域地下水水位（埋深）的预报方法，陈葆仁等（1988）做了系统的总结。主要的方法有地下水动力学方法、地下水均衡方法、数理统计方法和随机过程中时间序列分析方法。一般来讲，地下水动力学方法应用范围广，可对区域内各处或区域水位的分布以及区域整体的地下水水位的动态作出预报。在此基础上还能进一步对区域地下水水质做出预报，这将是建立PWS体系所采取的主要方法（详见后述）。对于后3种方法，一般仅能对区域某处或整体的地下水动态作出预报，很难达到PWS体系中对区域地下水水位分布动态进行预报的要求。但由于地下水均衡方法与数理统计方法，建模简单，求解容易，在一定范围内对其进行改进，还是可以应用于区域地下水水位分布动态预报的（王鹏文，1988；人民胜利渠灌区，1990）。具体改进方法简述如下：

1.水均衡模型　在某一区域，按照地学条件（G）与人为因素（L）不同进行子区划分。在每个子区内，根据影响地下水水位的水均衡要素，建立地下水均衡方程，见式（4.1）：

式中　μ：给水度；

Δt：时段（T）；

ΔH：时段内地下水水位变化（L）；

ΣQn：时段内补给地下水的总水量（LT-1）；

ΣQout：时段内地下水消耗总水量（LT-1）。

确定出方程（4.1）中的各因子，即可求出地下水水位在Δt时间内的变化ΔH。

为使（4.1）式能用于区内所考虑点位的地下水水位预报，人民胜利渠灌区（1990）采用如下改进方法，步骤为：

（1）建立子区内各点的地下水水位（观测值）与所在子区的平均地下水水位的统计相关关系方程；

（2）根据建立的相关关系方程与子区内平均地下水水位预报的结果，推算出每个点的地下水水位预报值；

（3）据每个点的地下水水位预报值，在区域范围内插值，绘制出区域地下水水位等值线预报图。

2.数理统计模型　根据气象条件（C）、地学条件（G）与人为因素（L）的变化，首先对研究的区域进行子区划分；其次，根据所考虑的预报时段或因子的季节性变化，对时段进行离散，建立起一定时段内地下水水位变幅或地下水埋深与气象因子（如降雨量、蒸发量、气温）与人为因子（如灌溉量）之间的多元相关方程。如（4.2）式所示：

式中　τ：所考虑时段；

d：地下水埋深。

或

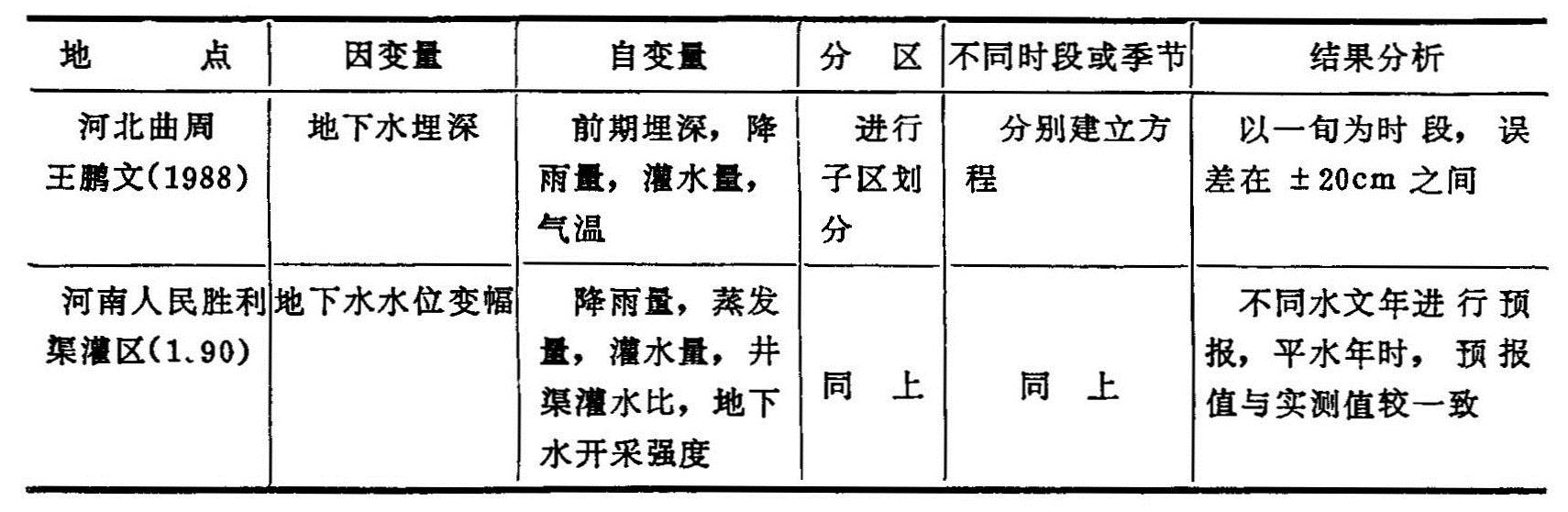
据式（4.2.1）或（4.2.2）即可对每个子区的地下水埋深或水位作出预报。综合各子区的预报结果，即可对区域地下水水位动态作出预报。王鹏文对曲周测报区（1988）以及人民胜利渠灌区对这方面的工作进行了报道。（见表4.1）

（二）数学模型的建立

通过对区域地下水水位预报方法的评述可知，在PWS体系中，欲对区域地下水水位动态进行预报，选用地下水动力学方法建模最为适宜，这归于地下水动力学模型，能够详细刻画出地下水系统随时间和空间的变化。所要研究的是对水动力学模型有关参数，与源汇项的处理作进一步的改进。

对地下水流方程，Bear（1979）巳作了系统的阐述。对于浅层地下水为潜水一微承压水系统，所建立的数学模型一般选用的方程为：

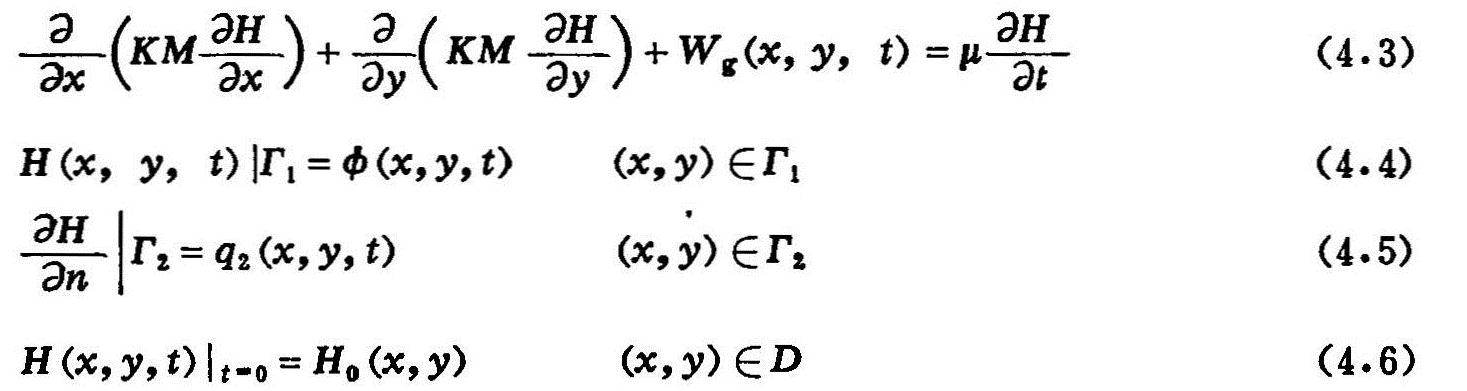
式中　H：地下水水位（L）；

x、y：笛卡尔坐标（L）；

M：第一稳定隔水底板以上沙层总厚度（L）；

K：渗透系数（LT-1）；

μ：给水度；

t：时间；

Γ1、Γ2：一类、二类边界；

D：测报区（研究区）域；

φ：水位或水头（L）；

q2：单宽流量（LT-1）；

n：Γ2边界外法线方向；

Wg（x，y，t）：地下水源汇项，即土壤水与地下水的变换量。

在地势较平坦的冲积平原区内，年内的地下水水位动态主要受Wg（x，y，t）的影响，K、M对其影响并不十分显著（薛禹群等，1979）。所以对Wg（x，y，t）处理的好坏就直接影响模型的预报精度。

Wg（x，y，t）相当于区域地下水水位预报概念模型中的r31·RWS（x，y）3（t）（见式2.23）。对其处理作如下考虑：在冲积平原区不同地学综合体类型（G）上，Wg（x，y，t）主要受气候条件（C）与土地管理因子（L）的控制。在中比例尺成图范围（几百平方公里）内，一般可把区域的气候条件（C）视为一致，而人为因素（L）在空间（x，y，t）分布差异较大，所以对其处理要考虑空间分布效应。从第二章的系统分析可知，C、L是通过G作用于区域水盐运动系统的，具体到地下水子系统是C、L先作用于土壤水，然后渗漏补给地下水，或受C的影响地下水补给土壤水再蒸散到大气中。这就说明Wg（x，y，t）在G不变时，主要受C、L的控制；另外也受到当前土壤水分含量的制约，这是由于土壤水与地下水是相互作用的。当研究的对象是1米土体的土壤水贮量时，由于1米以下土壤水含量比较稳定（鹿洁忠等1985），这样可作如下假定：当前土壤水分含量对Wg（x，y，t）的影响，可用前期地下水埋深d（t-1）对Wg（x，y，t）的影响来替换，即认为Wg（x，y，t）是C，G，L，RWS1（t-1）的函数。这样的转换就把地下水子系统与土壤水子系统的数学模型求解独立起来。

据上述分析，Wg（x，y，t）可根据下式求出：

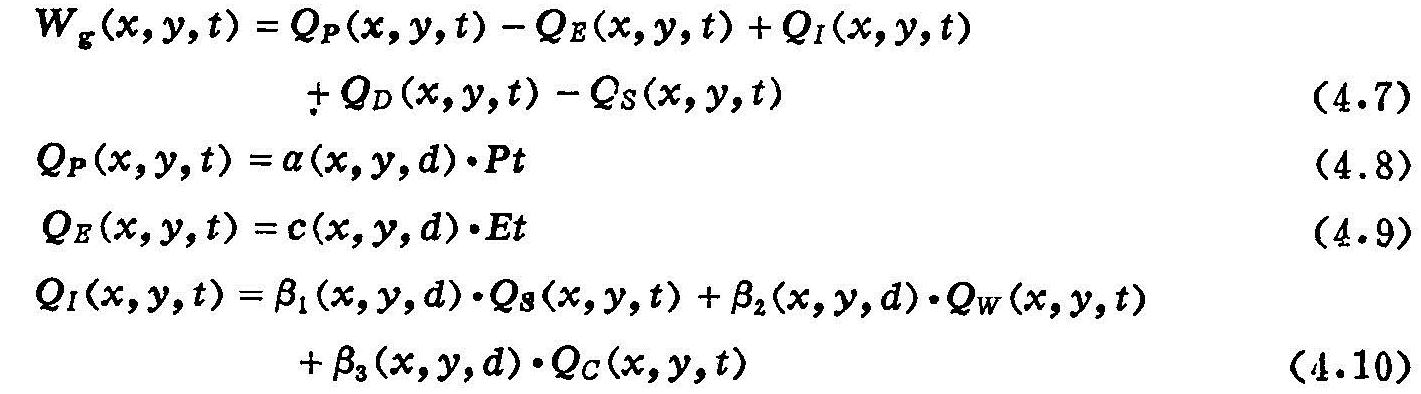
式中　P：降雨量（L）；

E：自由水面蒸发量（L）：

QP：降雨补给浅层地下水量（LT-1）；

QE：浅层地下水蒸发消耗量（LT-1）；

QI：灌溉补给地下水总量（LT-1）；

QD：大型渠道补给（+）、排泄（-）地下水量（LT-1）；

Qs：浅井开采水量（LT-1）；

QW：深井开采水量（LT-1）；

Qc：河渠灌溉量（LT-1）；

a：降雨入渗补给系数；

c：潜水蒸发系数；

β1、β2：浅井、深井灌溉补给地下水系数；

β3：渠灌补给地下水系数；

d：地下水埋深（L）。

下标（x，y，d）表示该参数受空间坐标（x，y）与地下水埋深（d）的影响。

（4.3）式至（4.10）式即为所建立的对区域地下水水位（埋深）进行预报的数学模型。

（三）数值方法的选择

对于式（4.3）仅能通过数值计算方法求解。现报道数值方法有限差分、有限元、边界元三种方法（薛禹群与谢春红，1980；孙讷正，1981，1989；张蔚榛，1983）。这3种方法中，边界元方法（BEM）在近几年来巳成为一种很有竞争力的算法，但其要求条件严格，在处理非均质、非线性、非稳定等复杂问题计算时效率大大降低（孙讷正，1989）；通常的有限差分与有限元方法业已成熟，但有限元方法与有限差分方法比较，具有网格剖分比较灵活、对边界条件处理也较容易等优点，而在求解地下水动力学方面的问题中越来越多地被采用（Pinder与Gray，1977；孙讷正，1981，1989）。基于此，在PWS体系中，所建立的地下水数学模型也宜采用有限元方法求解。

有关有限元方法求解地下水流方程的详细过程与原理，可参照有关专著或文献（薛禹群与谢春红，1980；孙讷正，1981，1989；张蔚榛11983；陈葆仁等，1988）。下面仅作一简单介绍。

把方程（4.3）转化为：

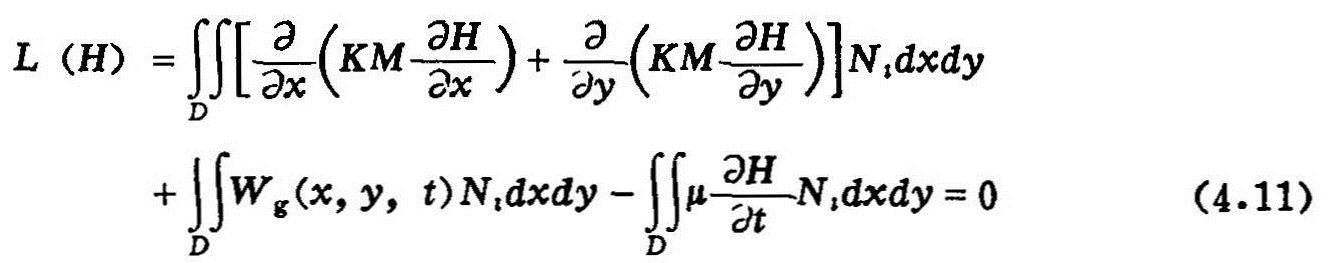
如区域采用三角形单元剖分，用L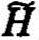（）近似L（H），其中对任一三角形：

据　Galerkin法则：

经一系列推导整理可得：

（4.14）式即为有限元法离散化后的数学模型。

式中［A（t）］：渗透矩阵或传导矩阵，它与有限单元的剖分、含水层厚度及渗透性能有关，即与地学综合体G有关；

［H］：结点水位，为一列向量；

［C］：贮水矩阵，也由G决定；

［F］：常数矩阵，由有限单元内Wg（x，y，t）及第二类边界补给流量组成。即由C，L，G共同决定。

对式（4.14）在时间上进行差分，形成线性方程组，可用LDLT等方法求解，即可得出测报区（D）中每一处在某一时刻的地下水水位H（x，y，t）或地下水埋深d（x，y，t）。另在模型求解过程中也可得到QP（x，y，t）、QE（x，y，t）、QI（x，y，t）、QD（x，y，t）、QS（x，y，t）等，这些将在地下水水质、土壤水盐预报模型中分别得到应用。