土壤盐分多离子耦合运移模型(CMDL)
CMDL模型的特点,是同时刻划了4个离子在同一土柱内相互连系、相互影响的耦合运动,考虑了盐分在土壤中运移时的化学反应,和离子交换或离子吸附等各源汇项因子。其中对参数的估计分两组进行,首先是各离子的扩散弥散系数,其次是吸附交换和源汇项参数的估计。
(一)模型的建立
在稳态饱和流条件下,土柱一端的盐通量J巳知,并假设:
①系统中只存在Ca2+、Na+、![]() 、Cl-四大离子;
、Cl-四大离子;
②只存在Ca2+与![]() 的化学反应,固体硫酸钙的比表面积不变;
的化学反应,固体硫酸钙的比表面积不变;
③只存在Ca2+的土壤胶体吸附或Ca2+、Na+的交换反应;
④温度恒定。
则CMDL可表示为:
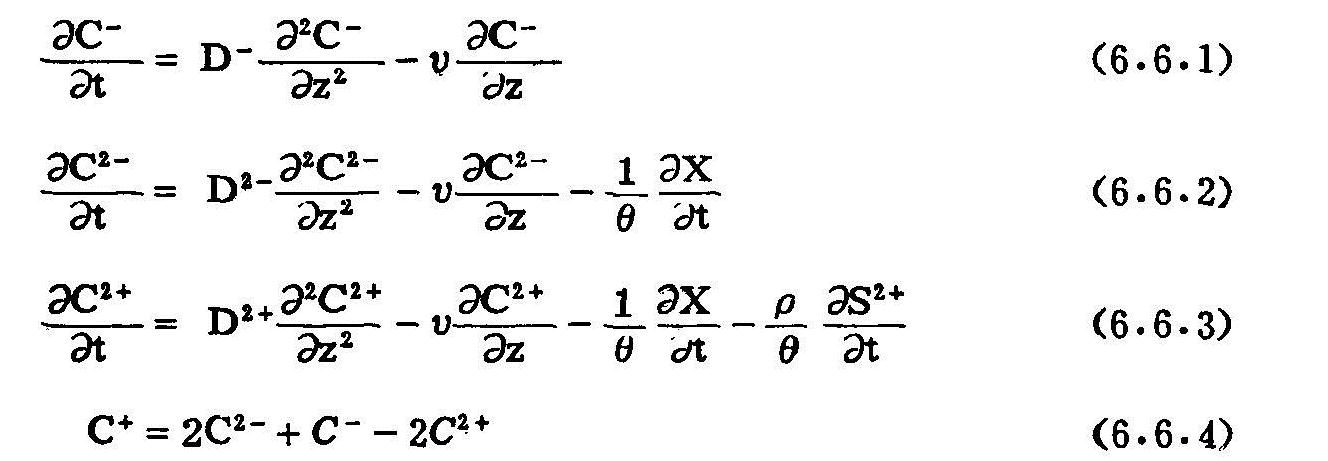
且满足以下初始边界条件:
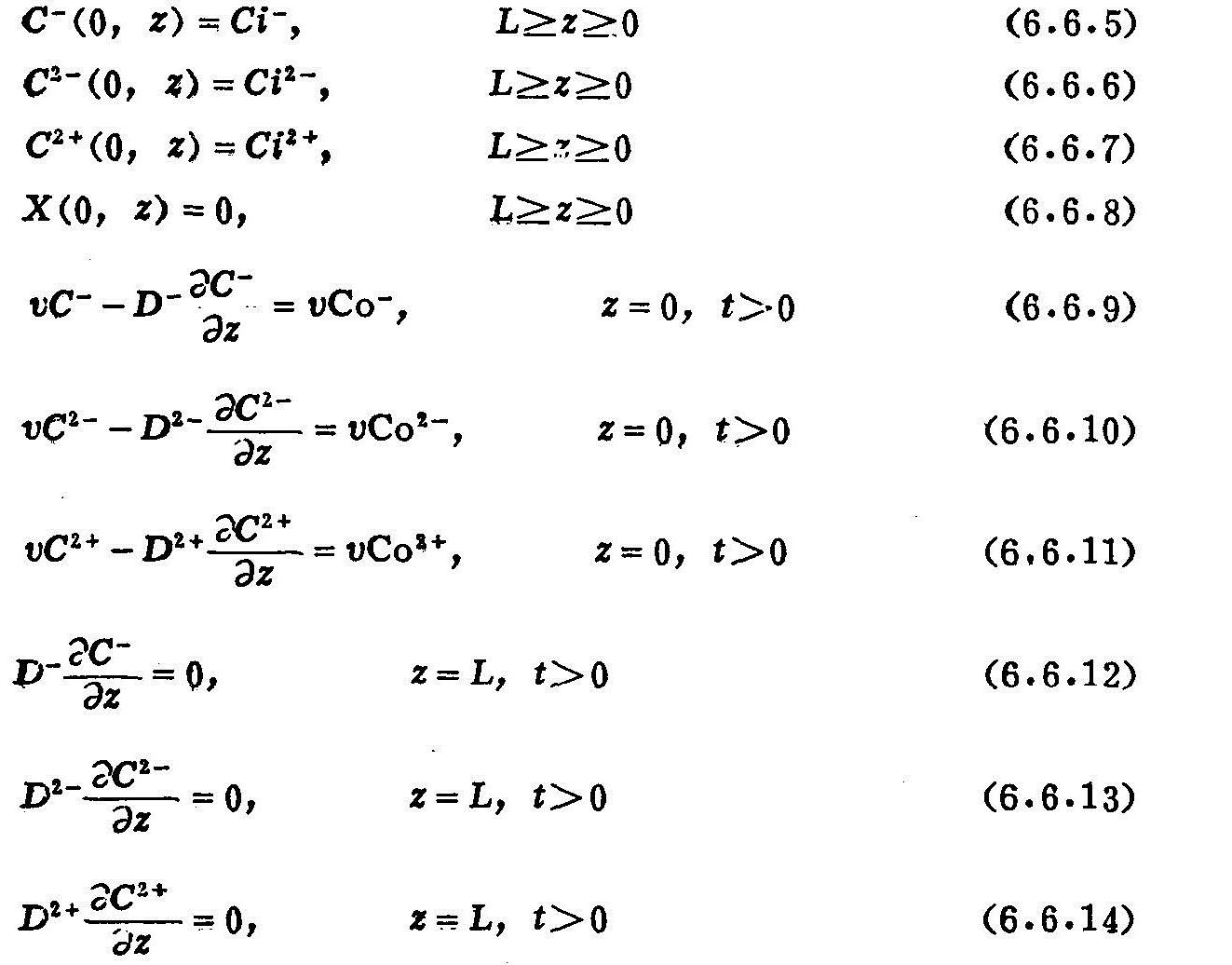
式中 角标2+、+、2-、-,分别表示Ca、Na、SO4和C1的电荷;
D:扩散一弥散系数(cm2h-1);
υ:孔隙水流速(cmh-1);
θ:容积含水量;
ρ:土壤容重(gcm-3);
z:距离(cm);
t:时间(h);
X:为CaSO4的沉淀量(moldm-3);
S:阳离子的交换或吸附量(molg-1);
L:土柱长度(cm);
C:土壤溶液中各离子的浓度(moll-1);
Ci和Co:土柱的原始溶液浓度和输入液浓度(moll-1)。
硫酸钙的沉淀与溶解
Ca2+与![]() 的化学反应满足溶度积原理,其反应方程可写成:
的化学反应满足溶度积原理,其反应方程可写成:
反应速度属于二级动力学过程,假定满足:
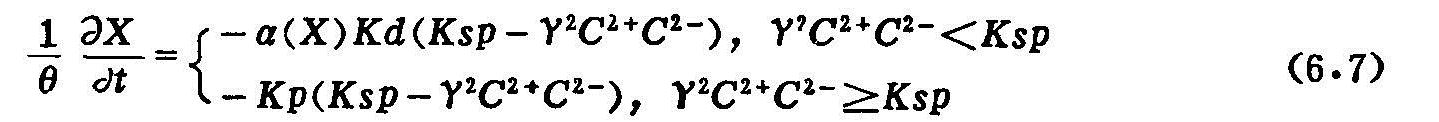
式中 Ksp:溶度积常数;
Kd:溶解常数(1mol-1h-1);
Kp:沉淀常数(1mol-1h-1);
a(X):单位跃迁函数,其值取
γ:活度系数。
活度系数γ的估计采用Davies方程:
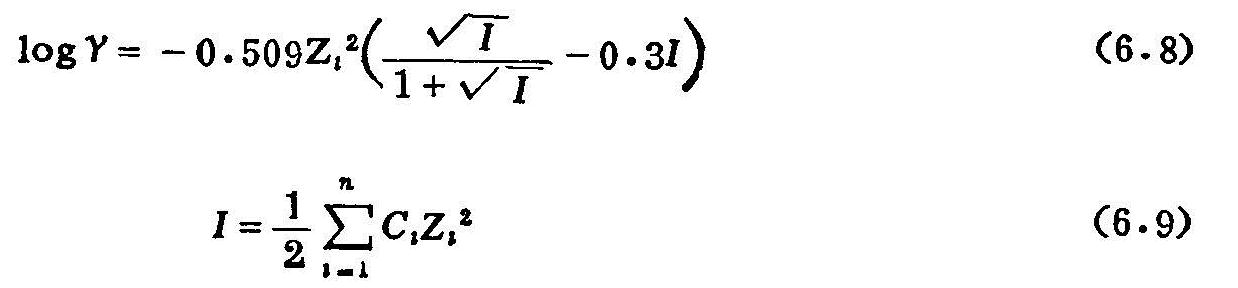
式中 I:离子强度;
Zi:离子化合价;
i:表示离子类别。
阳离子吸附
如果源汇项![]() 作为吸附反应来处理的话,可进一步假定它是瞬态平衡的过程,因此可用吸附恒温曲线来描述,选用Langmuir方程:
作为吸附反应来处理的话,可进一步假定它是瞬态平衡的过程,因此可用吸附恒温曲线来描述,选用Langmuir方程:
式中 M、K:吸附常数。
则:
代入式(6.6.3),并设
则得:
式(6.12)、(6.13)和前面的式(6.6.1)、(6.6.2)、(6.6.4)结合,构成有吸附和沉淀溶解作用下的CMDL。
阳离子交换作用
对于盐基饱和土壤,吸附作用往往很小,因为此时土壤胶体供吸附新的离子的剩余电荷巳微乎其微,而实际上离子代换过程却大量存在。溶液中一种离子的不平衡,势必影响到胶体表面其他离子的解吸与吸附的命运,即竞争的结果。
用a表示活度,设S2+符合离子交换模型:(https://www.daowen.com)
S2+=S2+(a2+,a+),
式中a2+和a+分别为Ca和Na在土壤溶液中的活度。说明土壤中交换性Ca2+是溶液中Ca2+和Na+活度的函数。
式(6.6.3)中的∂s/∂t项则可写成:
根据活度和浓度的关系,a2+=γ2+C2+,a+=γ+C+,将式(6.14)展开,得:
其中:
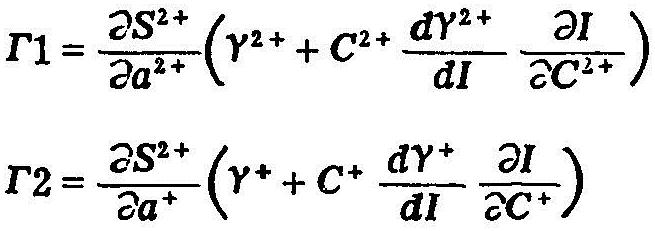
将式(6.15)代入式(6.6.3),最后得到下式:
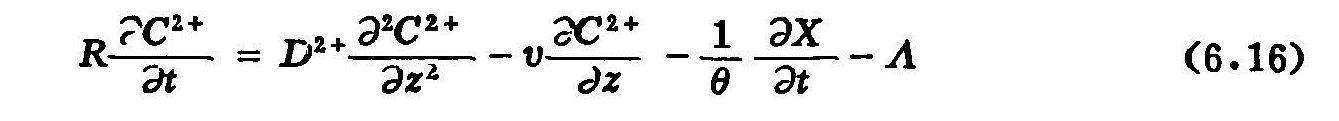
其中:
式(6.16)同式(6.6.1)、(6.6.2)和(6.6.4)构成了具有交换作用和溶解沉淀反应的CMDL模型。
为了确定Γ1和Γ2中各项的计算,可根据Gapon方程表示土壤中Na+、Ca2+离子的交换反应:
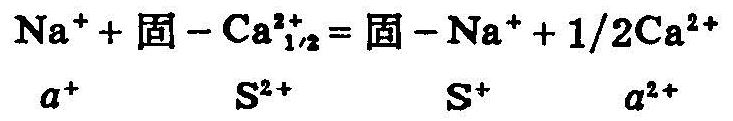
式中 Kg:为Gapon常数(1 mol-1)1/2,S2+的单位用molg-1(p+)表示。
由于S+=CEC-2S2+,代入式(6.17),整理后得:
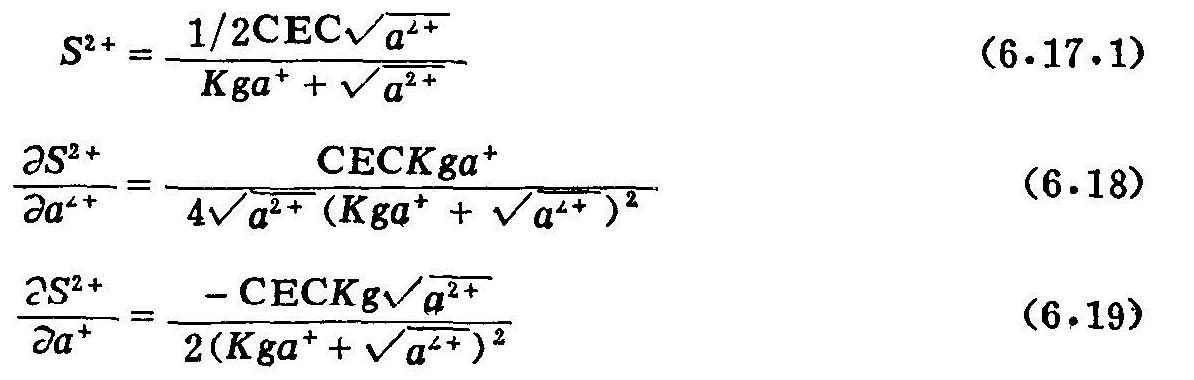
为了导出Γ1、Γ2中的其它各项,应用式(6.8)和(6.9),并用以下形式表示:
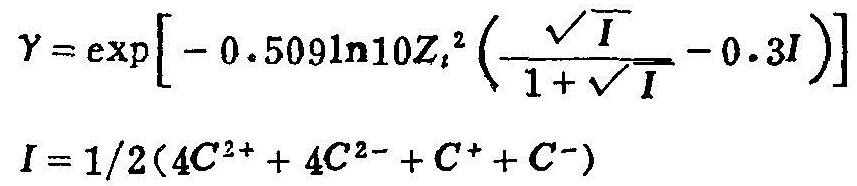
则dγ2+/dI和∂I/∂C2+等项可表示如下:
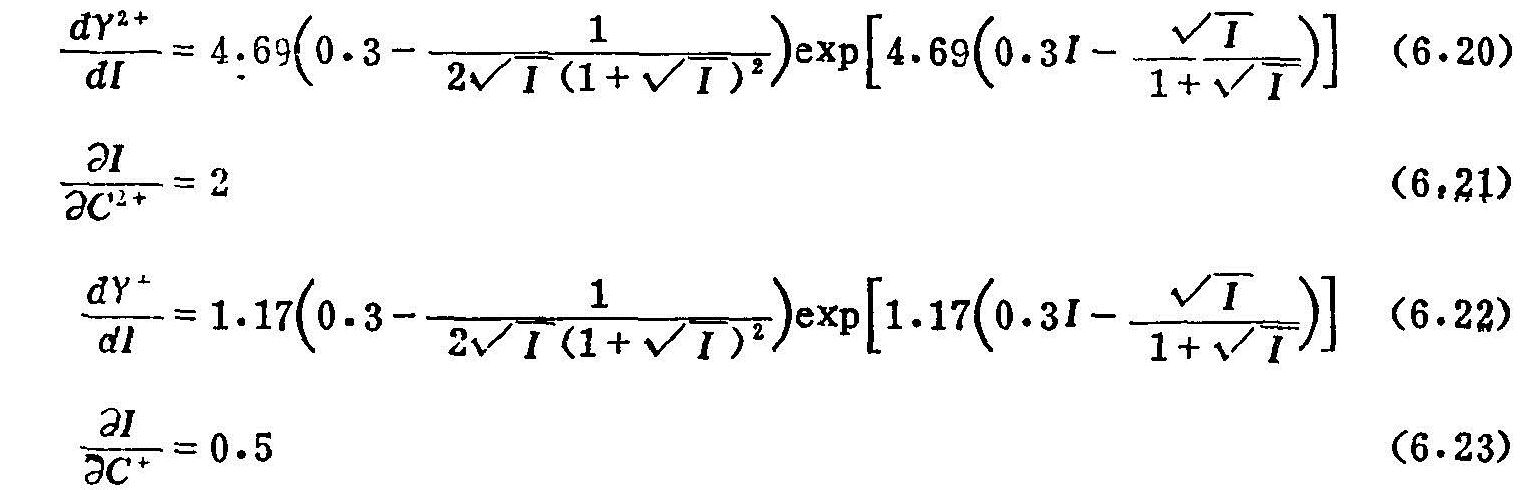
至此,式(6.16)中的R和Λ可以完全确定。
上述CMDL模型中,式(6.6.3)可以根据不同情况用式(6.13)(阳离子吸附)或式(6.16)(阳离子交换)代替,式(6.6.1)常采用解析解计算,式(6.6.2)和(6.6.3)常用数值解,用有限差分求解,选择Crank-Nicolson格式。源汇项因子可用显式差分求出。
(二)参数估计
试验描述
为了求得CMDL中的各项参数,进行了饱和土柱试验。土柱长30厘米,直径为4.8厘米。土壤为轻盐化均质壤土(曲周,巩村)。在稳态流条件下进行4种离子(Ca2+Na+,SO42-,Cl-)的易混合置换试验。
扩散-弥散系数的估计
C1-离子的D值较易求得,但与土壤最易发生作用的Ca2+和![]() 的D值求取较为困难,必须在没有源汇作用的条件下进行。因此在试验中设置以下条件:先用含Ca2+或
的D值求取较为困难,必须在没有源汇作用的条件下进行。因此在试验中设置以下条件:先用含Ca2+或![]() 的已知浓度溶液通过土柱,待流出液与流入液浓度一致时,可以认为Ca2+或
的已知浓度溶液通过土柱,待流出液与流入液浓度一致时,可以认为Ca2+或![]() 与土壤中的各种吸附或源汇作用基本趋于完成。然后用较高浓度的同一种溶液置换原溶液,测定流出液中Ca2+或
与土壤中的各种吸附或源汇作用基本趋于完成。然后用较高浓度的同一种溶液置换原溶液,测定流出液中Ca2+或![]() 的浓度,可以得到该离子的(C-Ci)/(Co-Ci)和流出液孔隙容积的穿透曲线。几种试验的基本情况可见表6.7。
的浓度,可以得到该离子的(C-Ci)/(Co-Ci)和流出液孔隙容积的穿透曲线。几种试验的基本情况可见表6.7。
表6.7 土柱试验的基本情况
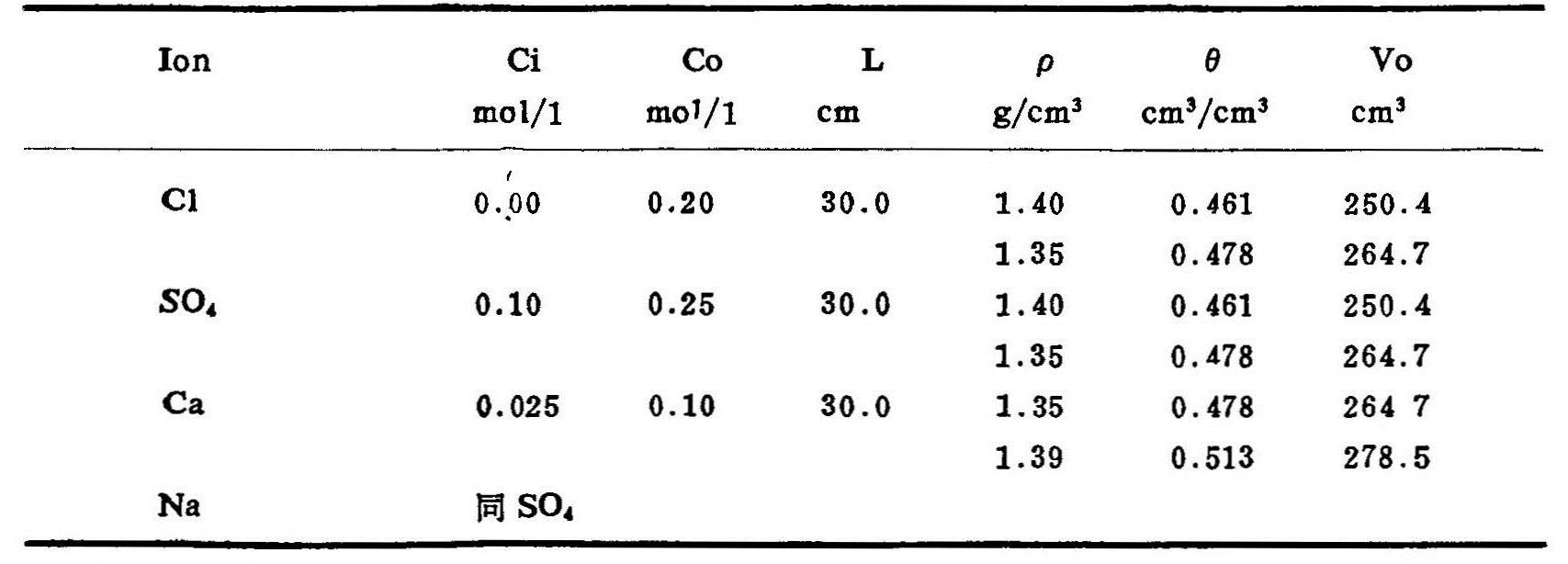
Vo:土柱中孔隙的容积。
由于是稳态饱和水流,溶质运动有解析解,选择与实测的穿透曲线拟合最好的参数D。由于D值直接测定困难,这种拟合的办法目前仍算是最有效的求参数方法之一。
稳态饱和流一维溶质运动方程(6.6.1),在式(6.6.5)—(6.6.14)条件下有解析,解。应用LM—NEWTON算法,其目标函数定为计算值与实测值的误差平方最小,即

其中C算由参数向量X所决定。向量X的各分号包括扩散弥散系数D、线性阻抑因子R及脉冲输入时的脉冲时间T等。
图(6.9.a-c)分别是Cl-、Ca2+和![]() 在没有源汇作用条件下的穿透曲线,用解析解拟合的部分结果,实测值与计算符合很好。其中C1-的穿透曲线是用脉冲输入的形式做成的。不同流速条件下拟合得到的D值(图6.10),可以回归得到D与流速V之间的经验关系:
在没有源汇作用条件下的穿透曲线,用解析解拟合的部分结果,实测值与计算符合很好。其中C1-的穿透曲线是用脉冲输入的形式做成的。不同流速条件下拟合得到的D值(图6.10),可以回归得到D与流速V之间的经验关系:
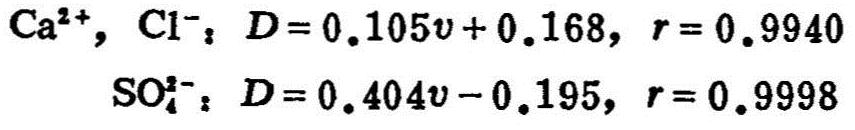
吸附参数的估计
先用0.5mol1-1HCl除去土中的CaCO3,再用0.1mol1-1HCl洗去交换性钙,最后用无离子水洗去Cl-至无AgCl沉淀。
Ca2+吸附速率试验:称5g无Ca2+风干土于离心管中,加入0.05moll-1CaCl225 cm3,分别按10′、20′、30′、45′、1h、2h振荡后立即离心取上清液,分析其Ca2+浓度。
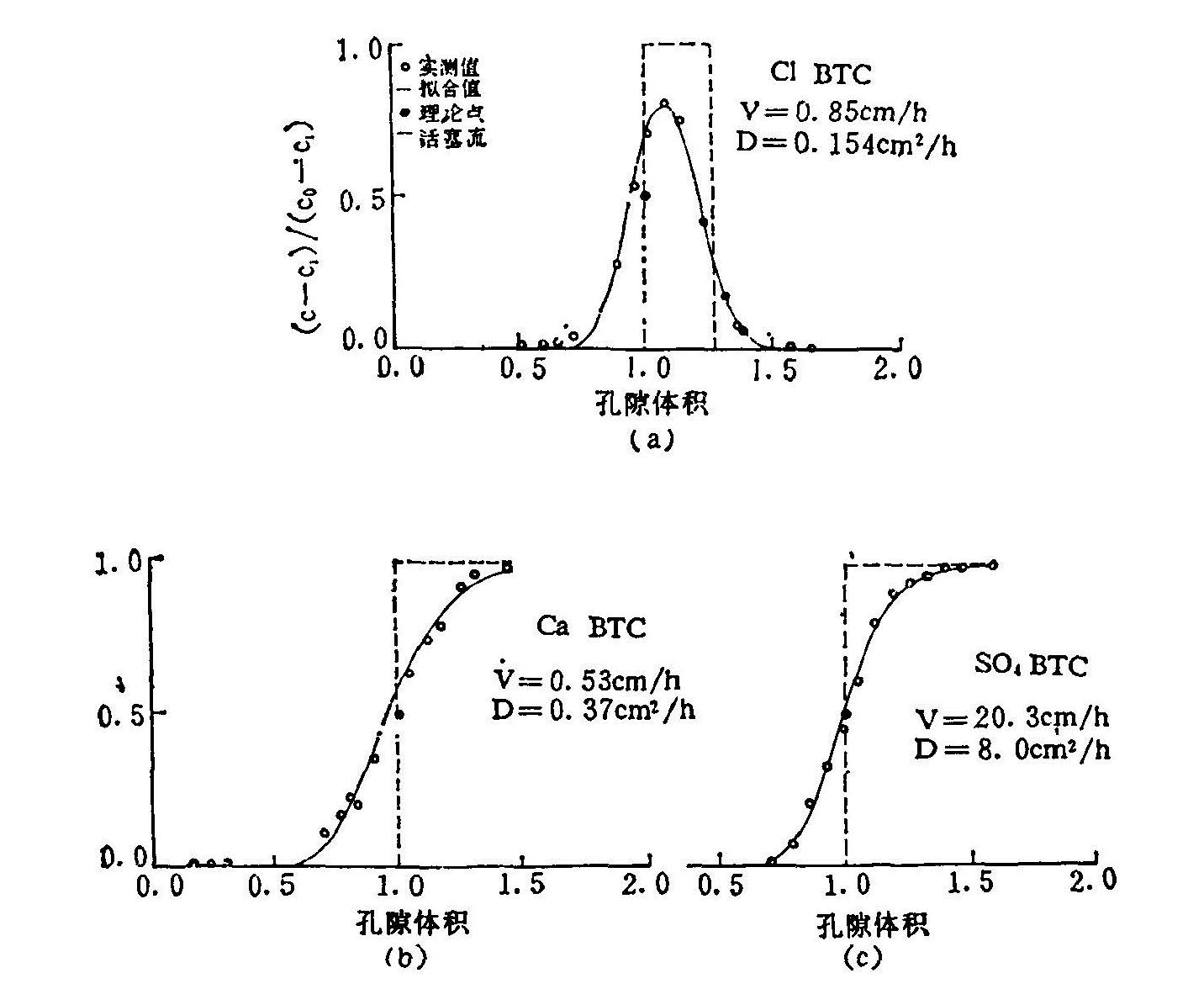
图6.9 用非线性最小二乘拟合法所得的Cl-、![]() 和Ca2+穿透曲线(BTC)
和Ca2+穿透曲线(BTC)
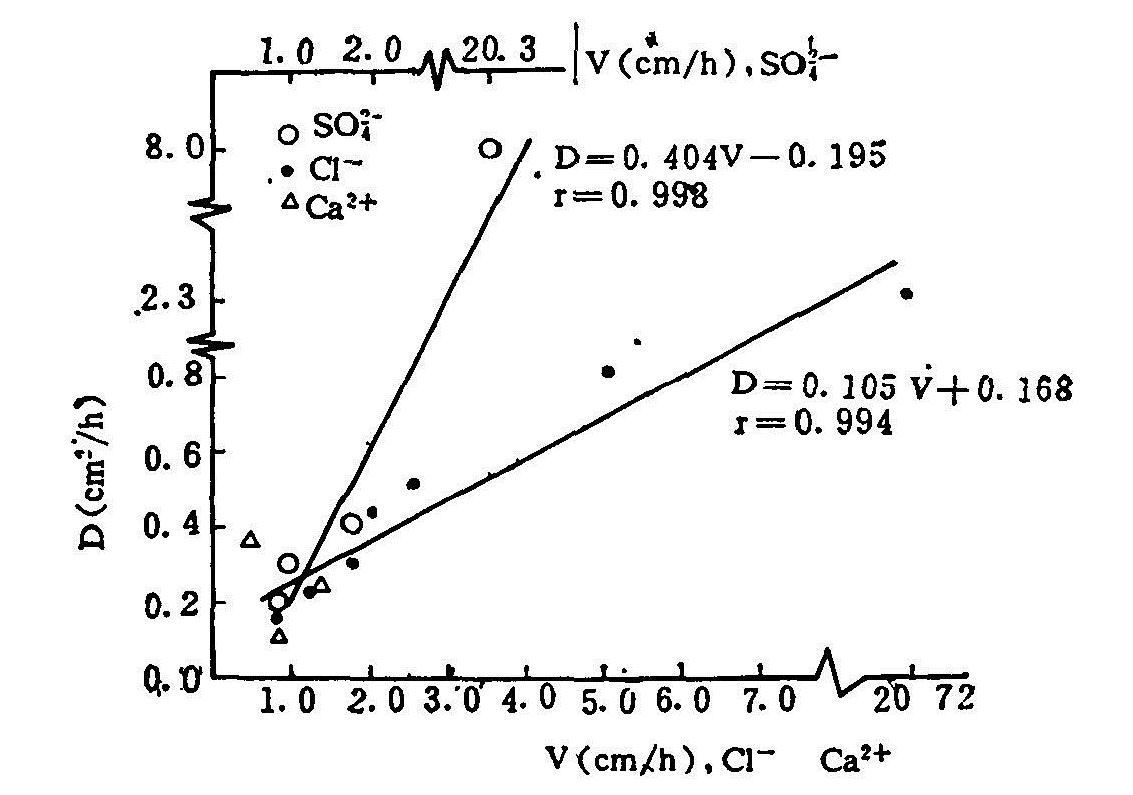
图6.10 土壤扩散弥散系数D与平均孔隙流速的关系
Ca2+的吸附平衡试验:称5g无Ca2+和未洗Ca2+土各数份,分别加入不同浓度的Ca2+标准液25cm3,振荡30分钟后静置24小时过滤,分析其Ca2+浓度。
试验结果表示于图6.11。
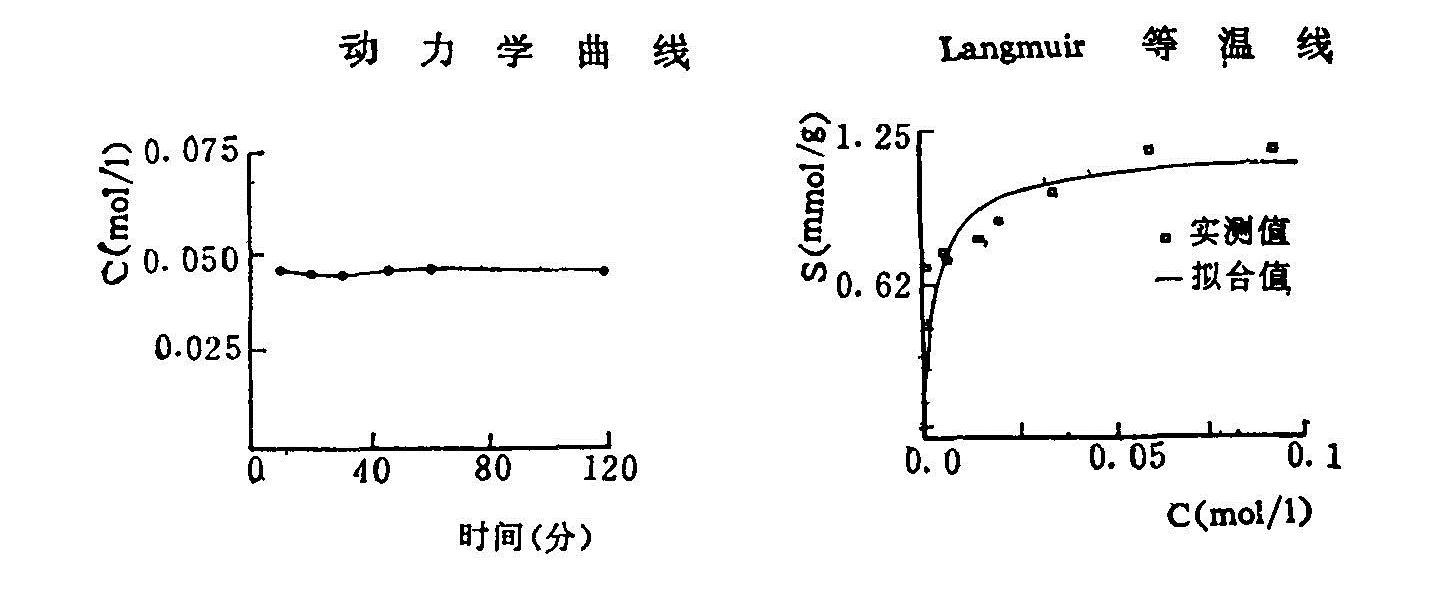
图6.11 曲周县巩村壤土Ca2+的动力吸附曲线(左)和等温吸附曲线(右)(1987)
图6.11左图很明显地证实了土壤对Ca2+的吸附是瞬态平衡的。土壤与其共存的溶液浓度几乎不随时间而发生改变,所以这种极快的平衡相对于Ca2+在土壤中缓慢的移动来说,其动力学性质是可以忽略的。
图6.11右图是洗钙土经过Langmuir方程拟合的结果,k值为0.287,m=1.1mmolg-2相关系数达到0.997的极显著水平。但是未经洗钙土样的恒温吸附结果说明,原自然土壤的吸附作用极微,当溶液浓度低时甚至释放Ca2+,其k值为0.564,m=0.17mmolg-1。
化学反应和交换参数
为了估算源汇项参数Kd、Kp和Gapon常数Kg,特设置了Ca2+存在下的![]() 淋洗试验。将0.1moll-1CaCl2均一后的土柱,用0.1mol1-1Na2SO4淋洗,得到
淋洗试验。将0.1moll-1CaCl2均一后的土柱,用0.1mol1-1Na2SO4淋洗,得到![]() 的穿透曲线和Ca2+的淋洗曲线。
的穿透曲线和Ca2+的淋洗曲线。
由于有源汇项的CMDL模型只能通过数值方法求解,建立起的CMDL的目标函数(同式6.24)Ψ的梯度和Hesse矩阵是难以求得的。因此必须寻求一种直接的方法避开目标函数的求导。单纯形代替法便能满足这一条件。它用式(6.24)作为目标函数,CMDL作为它信息函数值Ψ的子模型,以Kp、Kd和K 为自变量,先构造一个初始的多面体S(1),然后逐次构造一系列的多面体S(K)(K=2,3……),使S(K)不断地向函数Ψ(X)的极小点运动,最后获得满足极小要求的一个解向量Xmin,Xmin的各分量,就是Kp、Kd、Kg和Ksp。
为自变量,先构造一个初始的多面体S(1),然后逐次构造一系列的多面体S(K)(K=2,3……),使S(K)不断地向函数Ψ(X)的极小点运动,最后获得满足极小要求的一个解向量Xmin,Xmin的各分量,就是Kp、Kd、Kg和Ksp。
图6.12是用流速1.276cm/h的土柱实测值拟合求参数的结果。其中,Kp=8.01mol-1h-1,Kd=0.321molh-1,Kg=0.5(1mol-1)1/2,Ksp=4.2×10-4(moll-1)2。
以上所得Kg=0.5(1mo1-1)1/2相当于0.0158(1mmol-1)1/2,与美国盐渍土实验室报道的Kg=0.01-0.015(lmmol-1)1/2十分接近。
需要说明的是,本实验假设土柱中原始的固态CaSO4不存在,只是在灌入![]() 或Ca2+后才发生CaSO4沉淀的,且认为沉淀后的CaSO4呈大小一致的颗粒。自然土壤的固体CaSO4以结晶状态非均匀分布于土壤剖面中,这种情况下Kd可能会与结晶颗粒大小有关。
或Ca2+后才发生CaSO4沉淀的,且认为沉淀后的CaSO4呈大小一致的颗粒。自然土壤的固体CaSO4以结晶状态非均匀分布于土壤剖面中,这种情况下Kd可能会与结晶颗粒大小有关。
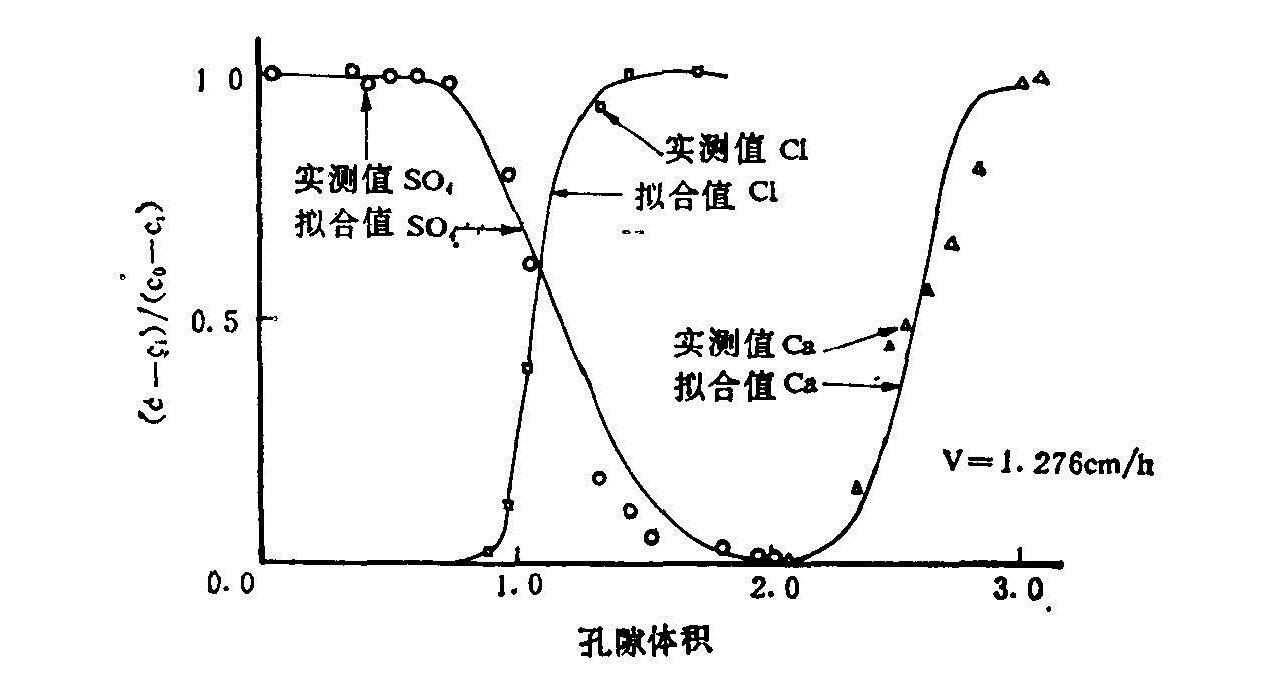
图6.12 试验土柱中用0.1moll-1CaCl2置换0.1mol1-1Na2SO4的易混合置换试验拟合结果
(三)模型的应用与讨论
在应用CMDL模型和用以上参数计算其他试验时,则涉及到究竟是用有吸附项的CMDL,还是用有交换项的CMDL;如用吸附项CMDL,是用去钙的参数,还是用未去钙的参数。为此作了对比计算,用实测值作为检验标准。
1.吸附参数的应用 用去钙和未去钙的两组k,m参数进行计算比较,其结果见图6.13和图6.14。
由图6.14与图6.15的比较可以看到,用去钙处理的吸附参数(k=0.287,m=1.1),计算结果与实测值相距甚远。计算值(实线)在整个实验阶段都降不下来,似乎Ca2+淋洗不尽。同时,硫酸根离子的流出锋面却迟迟难得出现,实测值与计算值符合得相当差。这种现象似乎说明土壤对Ca2+有极大的缓冲容量,表现在Langmuir方程中参数m值偏大。
采用未经洗钙处理测得的m值来进行计算,此时m值比图6.14中的要小。结果表明,符合效果要比图6.14好,但仍不尽如意。
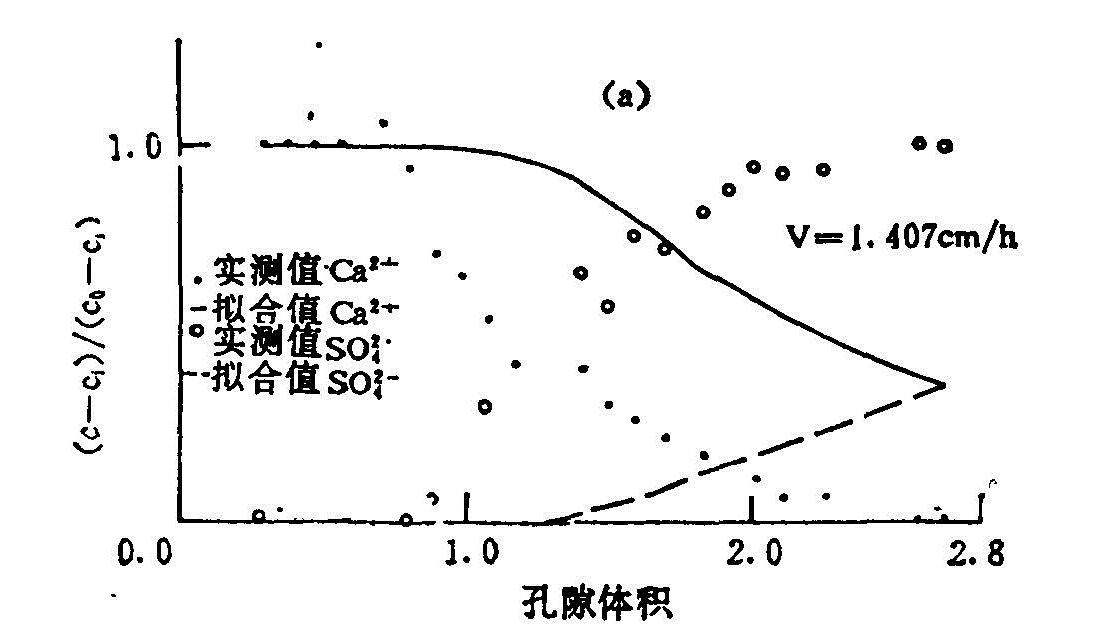
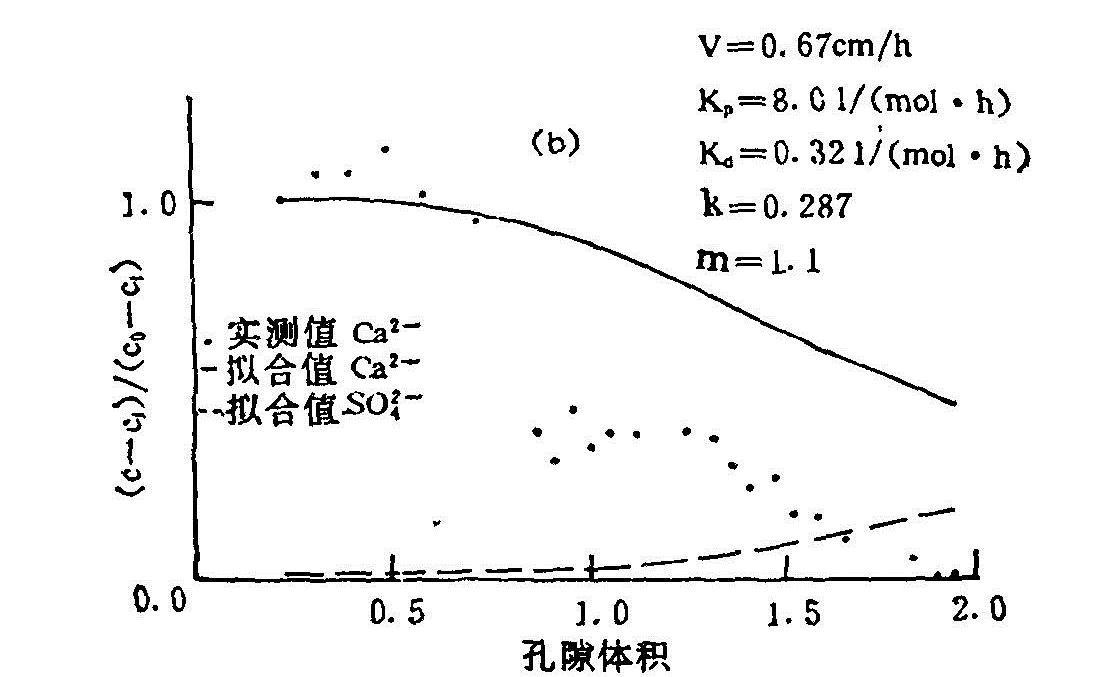
图6.13 用0.1moll-1Na2SO4置换0.1moll-1CaCl2时,Ca2+和![]() 的计算和实测穿透曲线(用有阳离子吸附项耦合模型的数值解和去交换性Ca的土壤参数)
的计算和实测穿透曲线(用有阳离子吸附项耦合模型的数值解和去交换性Ca的土壤参数)
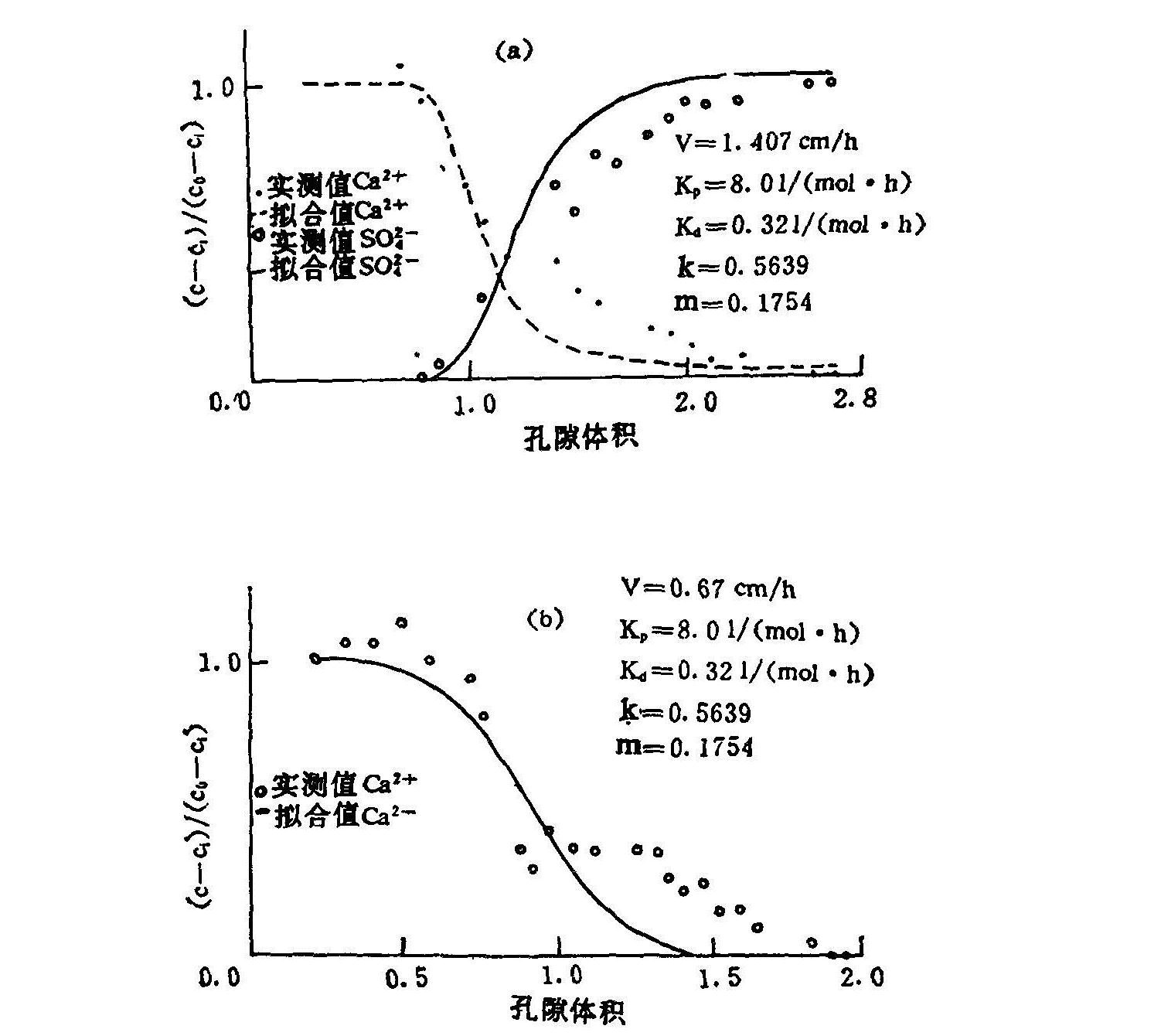
图6.14 用0.1moll-1Na2SO4置换0.1mol1-1CaCl2的Ca2+和![]() 的计算和实测的穿透曲线(BTCS)(用有阳离子吸附项耦合模型的数值解和未经洗钙处理的土壤参数)
的计算和实测的穿透曲线(BTCS)(用有阳离子吸附项耦合模型的数值解和未经洗钙处理的土壤参数)
说明用吸附方程的CMDL计算时,用符合实际土壤状况的未洗钙吸附参数的效果要好得多。
2.交换项的应用 应用有交换项的CMDL模型计算与图6.13,图6.14中a、b相同的实验,其结果表示于图6.15。
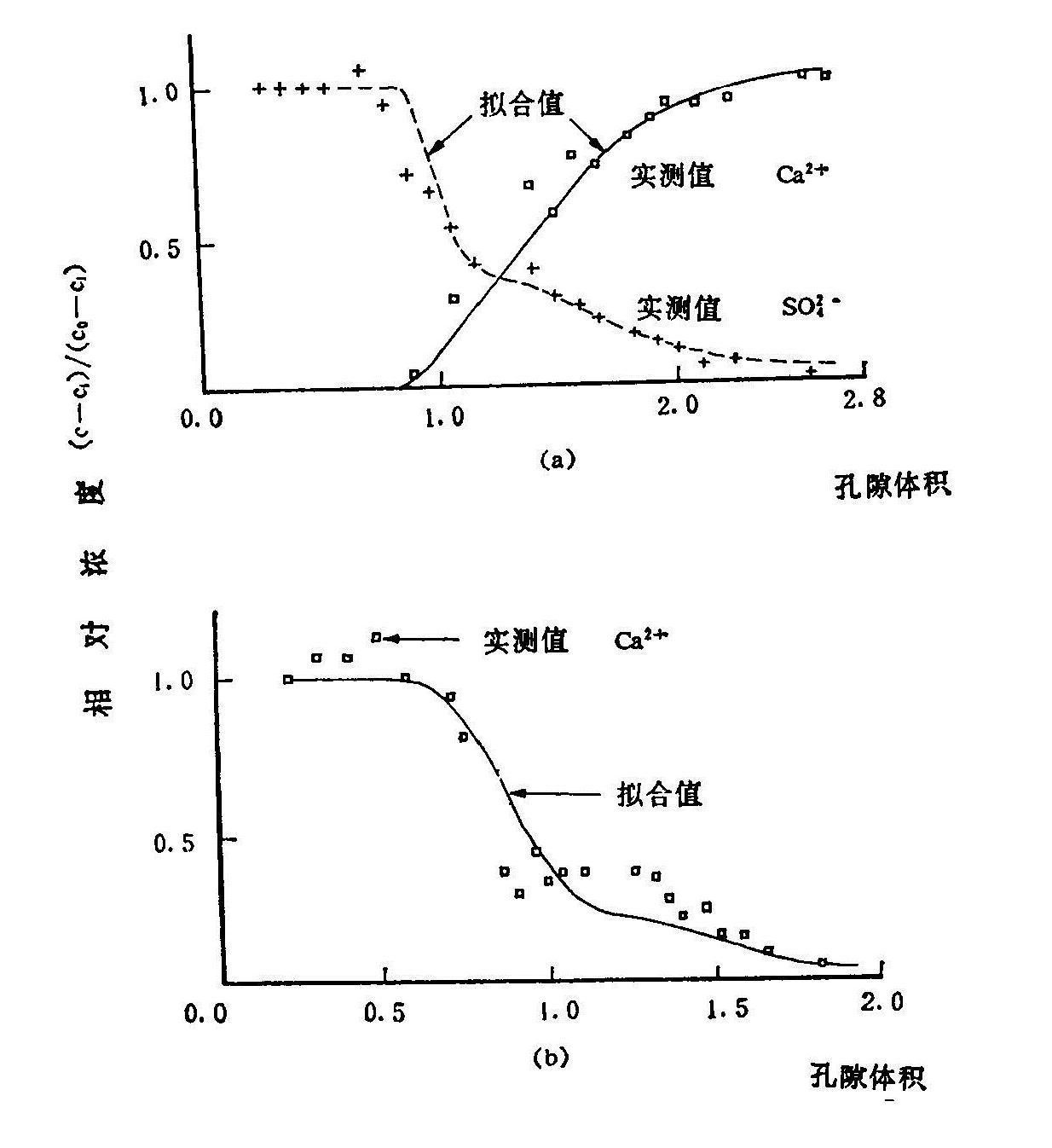
图6.15 用有阳离子交换项和溶解沉淀项的CMDL耦合模型的计算结果与实测值的对比
图6.15中计算值与实测值的符合程度令人满意。与图6.14中的a和b相比,进了一步。说明Langmuir方程是一个非竞争性的吸附方程,即吸附量与其平衡液中自身浓度有关,不受别的影响。这对于象农药、污染物等或许是有效的,但对于在土壤中同时存在多种阳离子时的钙离子而言,则不太合理。
溶液中的Ca2+要想被土壤胶粒吸附,势必遭到其他离子的竞争。Gapon方程刻划了这样的一个一价阳离子与二价阳离子间的竞争过程。图6.15的结果说明了在离子运移过程中考虑阳离子交换过程比用离子吸附作用更为合理。
在应用有交换项的CMDL模型计算时,试算了Gapon常数K 对计算结果的影响(图6.16)。
对计算结果的影响(图6.16)。
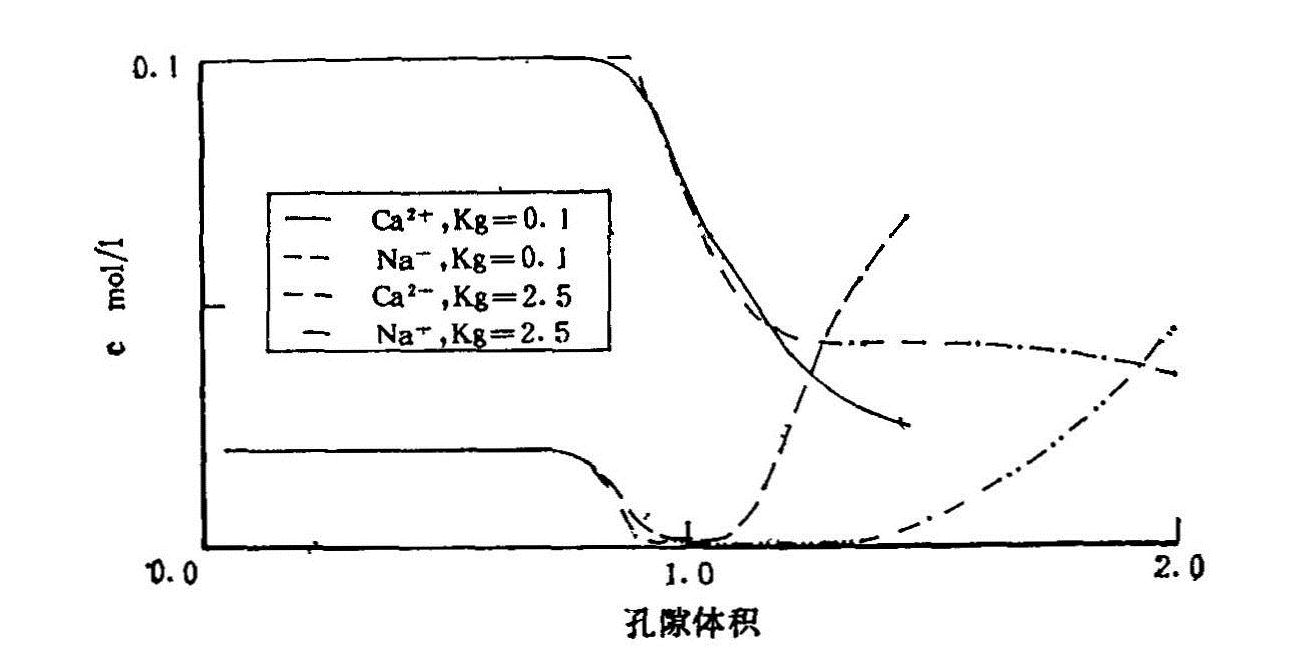
图6.16 Kg对Ca2+和Na+出流曲线的影响(巩村壤土,1987)(用有阳离子交换项的耦合模型的数值解)
图6.16说明了Gapon常数Kg对Ca2+和Na+传输过程的影响。由Gapon方程可知,Kg越大,Na+代换Ca2+的能力就越大,图6.16反映了这种趋势。当Kg=0.1时,Na+的浓度在Ca2+浓度下降后只稍有下跌,便开始迅速回升,表明胶体对Na+的吸附作用不大,很快就被输入的Na+补充并上升。相应地,Ca2+浓度在Kg取0.1时,被胶体吸附得更强烈,从而具有更大的缓冲性能。
3.溶解沉淀项参数的影响 图6.17、图6.18表示了化学沉淀系数Kp对CMDL计算结果的影响。对于淋洗锋面(图6.18),Kp从3.0增大到10.0时,锋面进一步变陡,整个曲线提前,但当Kp从10.0再加大到15.0时,整个曲线则几乎近于不再变化。穿透锋的情况(图6.17)与之相近,开始Kp从3.0增大到10.0,曲线变陡明显,且锋面进一步滞后(拖尾)。而当从10.0变化到15.0时,虽然锋面仍有所变陡,但不如开始显著。
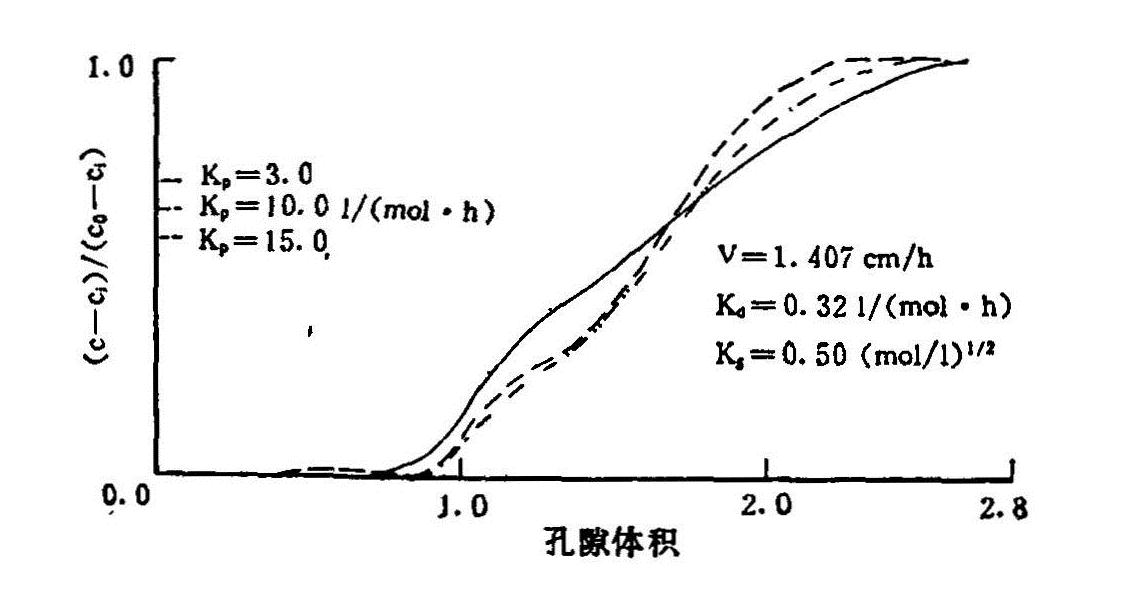
图6.17 Kp对硫酸盐穿透曲线的影响(曲周巩村壤土,1987)(用有阳离子交换项的耦合模型的数值解)
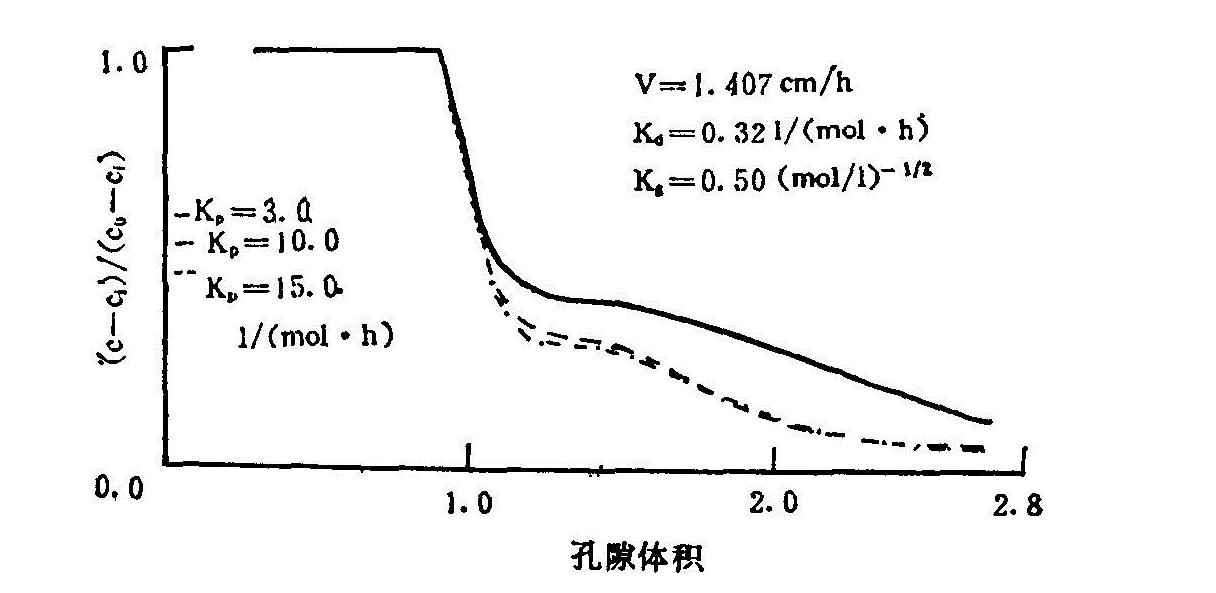
图6.18 Kp对钙离子出流曲线的影响(曲周巩村壤土,1987)(用有阳离子交换项的耦合模型的数值解)
上述影响说明,化学沉淀作用在溶质运动过程中的影响虽然很大,但是有一定限度的。试想,一个![]() 的运动锋面一旦碰上Ca2+的溶液,便开始在锋面发生沉淀,使锋面移动受阻和变形。但是源源不断地
的运动锋面一旦碰上Ca2+的溶液,便开始在锋面发生沉淀,使锋面移动受阻和变形。但是源源不断地![]() 溶液输入,仍足以使锋面向前推进。如果沉淀速度大到一定程度,使
溶液输入,仍足以使锋面向前推进。如果沉淀速度大到一定程度,使![]() 一遇到Ca2+便在瞬间完成反应,这时如再加大Kp,实际上是没有作用了。所以Kp从0逐渐加大,其对CMDL模型的影响程度应该是逐渐减小的。
一遇到Ca2+便在瞬间完成反应,这时如再加大Kp,实际上是没有作用了。所以Kp从0逐渐加大,其对CMDL模型的影响程度应该是逐渐减小的。
