农田土壤水量均衡模型的预报
(一)土壤水量均衡模型的建立
根据土壤水量均衡原理,一定土层时段内的贮水量应等于:
式中 W(t-1)3:时段初的贮水量;
P:时段内的降雨量;
IR:时段内的灌溉量;
ETa:时段内的蒸散量;
(Q下-Q上):时段内一定土层处的水通量;
R:地表径流量(单位均为毫米)。
如略去R,则:
当用降雨入渗补给量QP和灌溉回归量QI之和QPI,代替一定土层的累计向下水量Q下,用潜水蒸发量QE或用毛管上升量WG代替一定土层的累计向上水量Q上时,则(5.5)式可表达为:
或
如同时略去地面径流R和Q上(d>3.5米)时,则(5.5)式可简化为:
预报农田的土壤水状况,分别采用了(5.5.1)、(5.5.3)及(5.5.4)式。
(二)有关分量及参数的确定方法
(1)降雨量(P)。根据当地气象台站季度降雨趋势的预报及多年统计资料,给出降雨量分配的预报值,这是一个不易获得准确数据的分量。同时监测实际降雨量,用实测值检验预报值。
(2)灌溉量(IR)。根据区域水浇地的面积,主要作物(小麦、玉米、棉花)种植比例,及不同作物关键需水期的最佳灌溉方案,给出小麦全生育期灌三水,玉米灌一水,棉花视雨量分配情况确定是否灌溉。次灌水量定为90毫米(或根据1米土体达到田间持水量的需水量确定),同时用水表或根据抽水泵的出水率、灌水时间和田块面积求出实测值,用以检验预报值。
(3)地面径流量(R)。次降雨量大于80毫米时采取R=P-80,或忽略不计。
(4)实际蒸散量(ETa)。为一定土层供蒸发、蒸腾的耗水量。
ETa=Kc·Ks·E0
其中E0为潜在蒸散量,用彭门式计算或实测水面蒸发量代替(毫米);Kc为作物系数,参照陶祖文(1979)、王道龙(198G)的资料给出;Ks为土壤对农田可能蒸散需要水分的满足程度,即土壤系数,它和土壤贮水量、时段内的降雨量和灌溉量以及在大气因素影响下,土壤水分的消耗速率有关。Doorenbos(FAO,1977)推荐,在栽培地上Ks用土壤有效水分指数(ASI)表示,国内外不少学者曾用Wt/Wf、(Wt-Wp)/(Wf-Wp)和Wt/0.7Wf来代替Ks值。本研究据小麦在不同供水条件下,ETa与农田可能蒸散量ETm(ETm=Kc·E0)的比值,以及它们和产量的关系,确定以小麦水分利用率最高的ETa/ETm作为预报ETa的Ks值。玉米、棉花地的Ks根据旱涝指标的适合范围给出。
(5)一定土层下边界的垂直交换量Q下及Q上,用累计的下边界通量Σq给出。Σq=Q下+Q上,Q下为累计的向下通量,正值;Q上为累计的向上通量,负值。q可通过式q=K(h)·Δh/Δz求出,其中Δh/Δz与K(h)可通过田间布置试验测定给出。对区域土壤一定土层下行水量,用降雨入渗补给量与灌溉回归量之和QPI代替,正值;一定土层的上行水量,用潜水蒸发QE或毛管上升量WG代替,负值。那么QpI与QE或QpI与WG的代数和就为下边界通量。
(6)土壤初始水量(W(t-1))。通过实测取得。在连续预报中,下一阶段的初始值是上一阶段末的预报值。实测值还可应用于检验预报精度或修正某一时段的初始值。
(三)农田土壤水动态预报
(1)麦田不同灌水量条件下土壤水量均衡的预报:
①土壤水量预报模型选用(5.5.1)式。
②预报分量及有关参数,同麦田土壤水动力学预报参数。
③麦田不同灌水量条件下的水量均衡。
表5.11列出小麦不同生育期、不同灌水量条件下的水分均衡状况。
本区气候条件下,小麦生长季节的降雨量少,一般占土壤水收入量的20—25%以下。不足部分靠灌溉补充,灌溉量的大小直接影响到土壤水分的收入。最大的需灌水量,应是降雨不能满足的蒸散需水部分。麦季水分的支出项主要是蒸散,约占土壤水分支出项的80%以上或更高。供水量过高时,将引起土壤水渗漏,因入渗补给地下水,将使这一比例下降,使一次供水的利用率降低。如以供水量(降雨量与灌溉量之和)与田间耗水量之比(P+IR)/ETa,表示供水对作物需水满足的程度,以田间耗水量与水分支出项之比ETa/(ETa+Q下),作为水分渗漏剩余比,即供水补给土壤水的指标,(P+IR)/ETa的比值愈大,表示水分供应过多,将产生过量的渗漏和不能充分调动土壤水的调节作用。ETa/(ETa+Q下)的比值愈大,表示供水渗漏给1米土体以下的水分愈少,深层水对1米以上土体很难产生补给作用。试验麦田的地下水埋深为2.5—3.5米,从节约灌溉和充分调动土壤水的调节作用出发,宜将(P+IR)/ETa=0.85左右,ETa/(ETa+Q下)=0.8左右,作为麦田供水状况的适宜指标。
表5.11 麦田不同灌水条件下的水量均衡(mm,0—100cm土层)(1987)
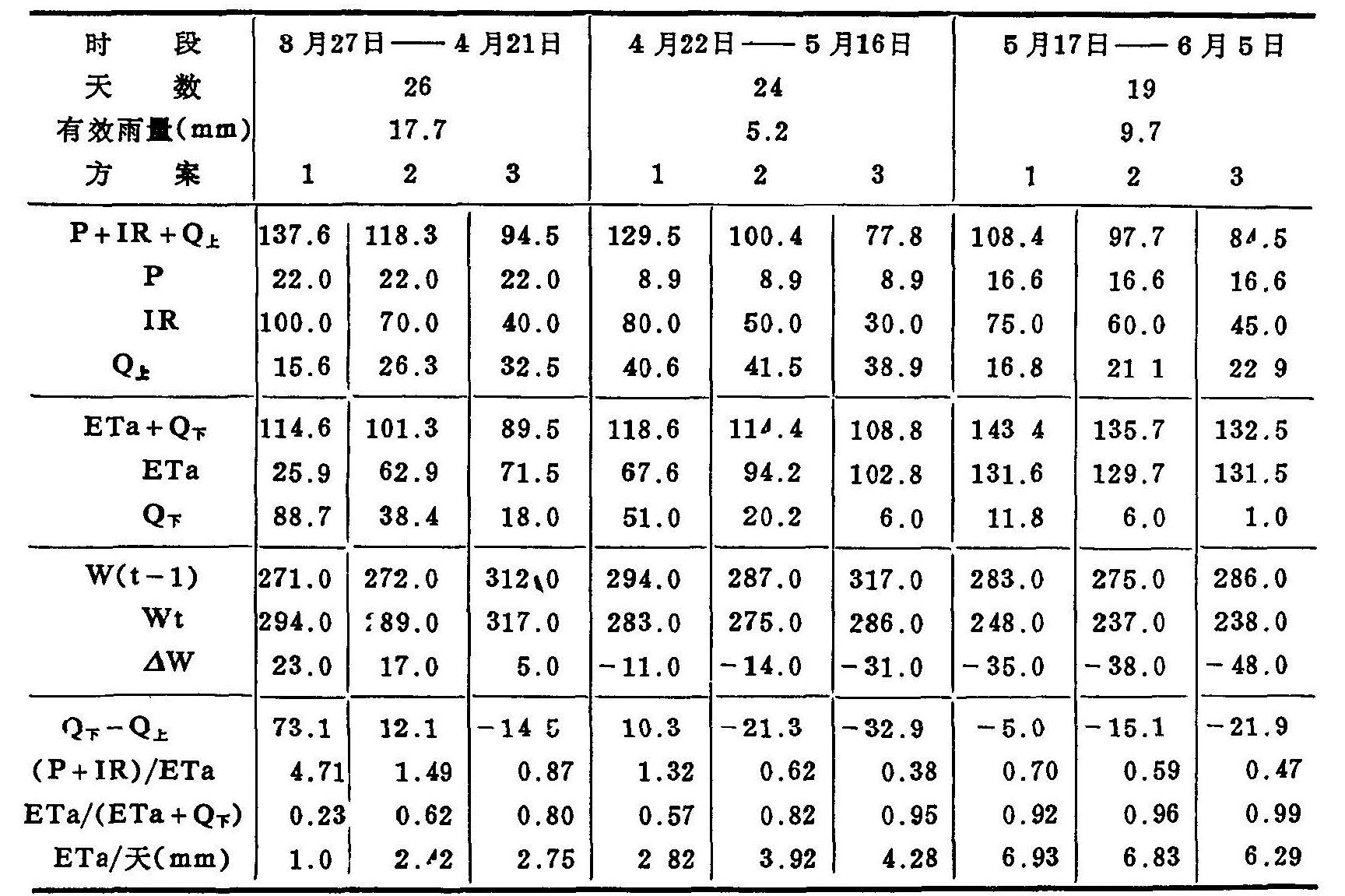
注:ETa=(P+IR+Q上-(Wt-W(t-1))-Q下
(2)农田土壤水量均衡状况的预报:
①土壤水量预报模型选用(5.5.3)式。
②预报分量及有关参数:
降雨量(P):采用时段内预报农田附近雨量站的监测数据。(见表5.12)(https://www.daowen.com)
表5.12 测报区内的降水量(mm)分布(1986.12—1987.12)
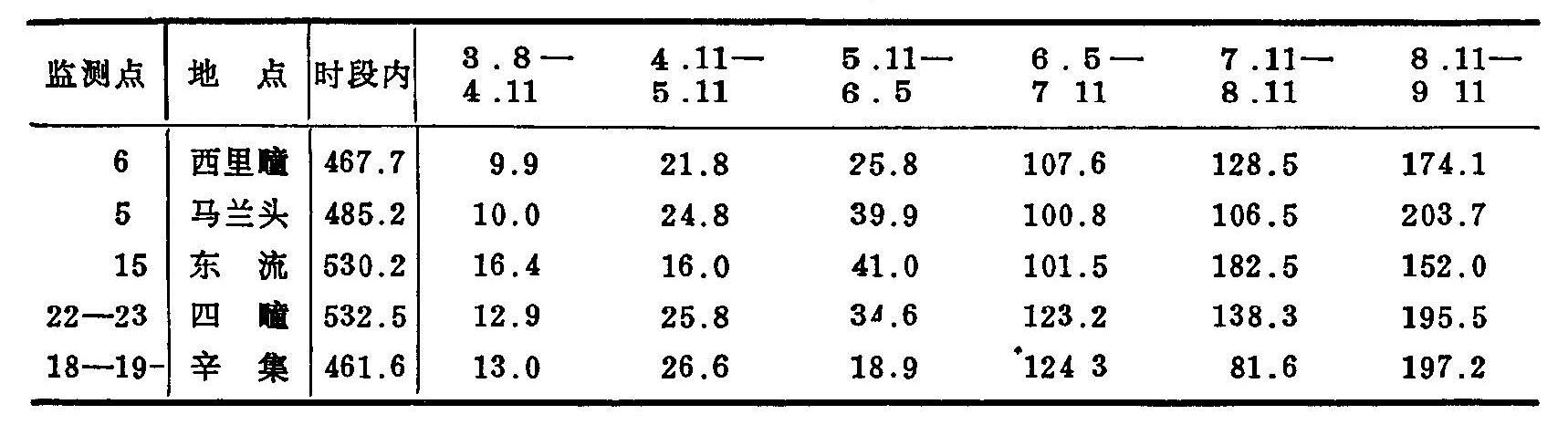
据测定,全区全年(1986.12—1987.12)平均降雨量为596毫米,预报时段内的降雨量占全年降雨量的77—89%。
灌溉量(IR):根据农田种植作物的灌水次数和时数,抽水泵的抽水速率估计。
蒸散量(ETa1):采用FAO 1979推荐的计算方法ETa=Ks·Kc·E0,E0取自林家栋等计算的曲周地区1966—1984年的月平均值(彭门修正式计算),见表5.13。Kc参考陶祖文(1979)对石家庄地区作物的给定值。(见表5.14)
表5.13 曲周历年月蒸发力平均值(E0)及其变异系数

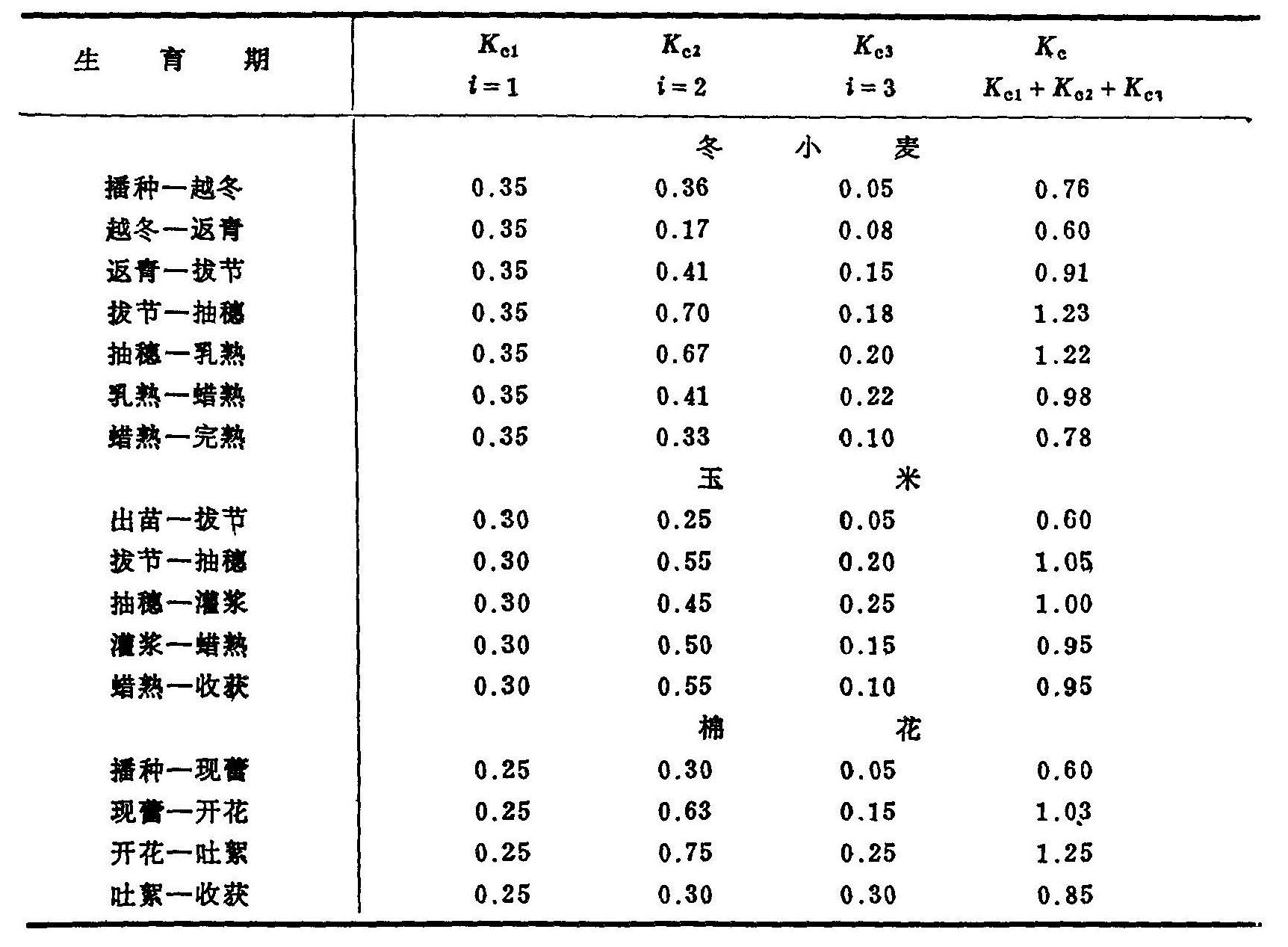
表5.14 不同作物不同生育期的作物系数Kc
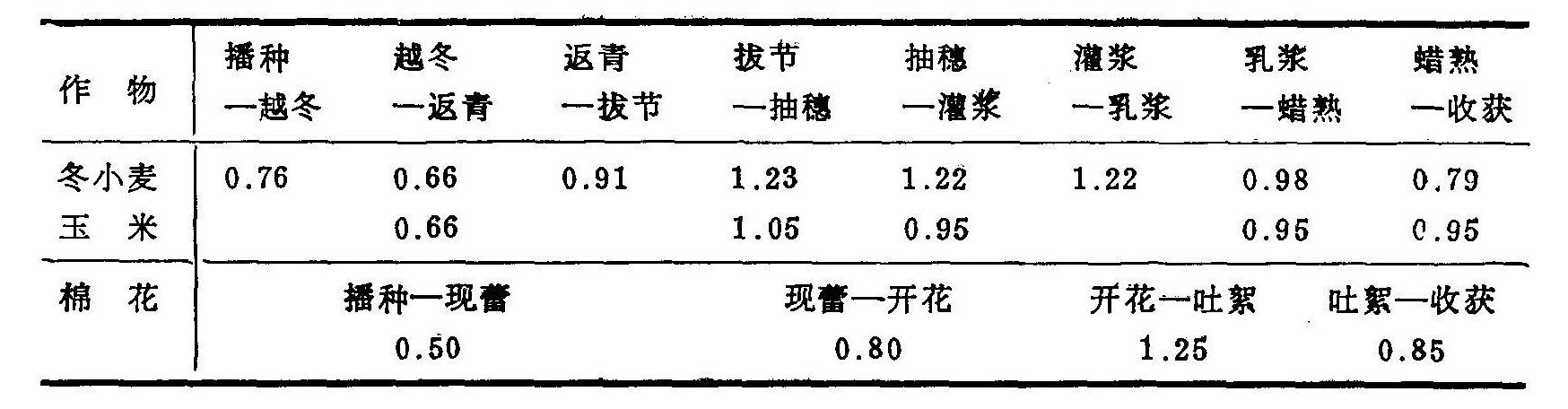
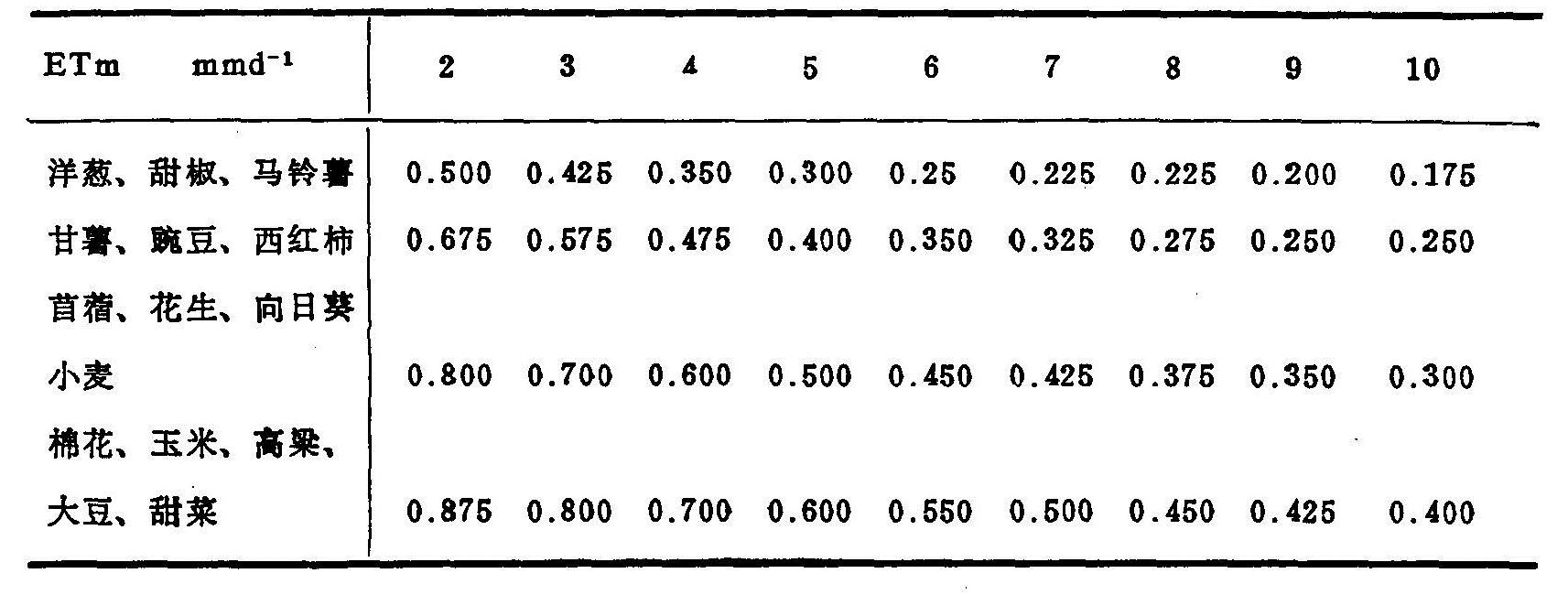
Ks采用FAO推荐的土壤有效水指数(ASI),ASI=(Pe+Ie+Wb-Wa)/ETm(月值),其中ETm为月农田可能蒸散量(毫米),Pe=P-R-Qp为有效降雨量(毫米);Ie=I-QI为纯灌溉用水量(毫米);Wb为月初一定土层(0—100厘米)中的有效水量(毫米),即Wb=W(t-1)-Wp;Wa为满足ETa=ETm后该土层的剩余有效水量(毫米),Wa=(1-Pm)·(Wf-Wp)(毫米),Pm=(Wm-Wp)/(Wf-Wp)、Wm为土壤中可供ETa1=ETm的土壤含水量(毫米),Pm为土壤中可供ETa1=ETm时有效水量占总有效水量的分数。因此,Wa为ETa1<ETm时的土壤有效水量,FAO提供的不同作物不同ETm条件下ETa1=ETm时的相对有效含水量,Pm(见表5.15)。
表5.15 不同作物不同ETm条件下的Pm值(FAO,1977)
当ASI>或=1时,实际蒸散量等于农田可能蒸散量,ETa1=ETm;当ASI<1时,只有在Wa很高和ETm非常小时才能出现;当ASI介于零与1之间时,FAO提供的ETa与ASI、Wa及ETm的相关数值列于表5.16。
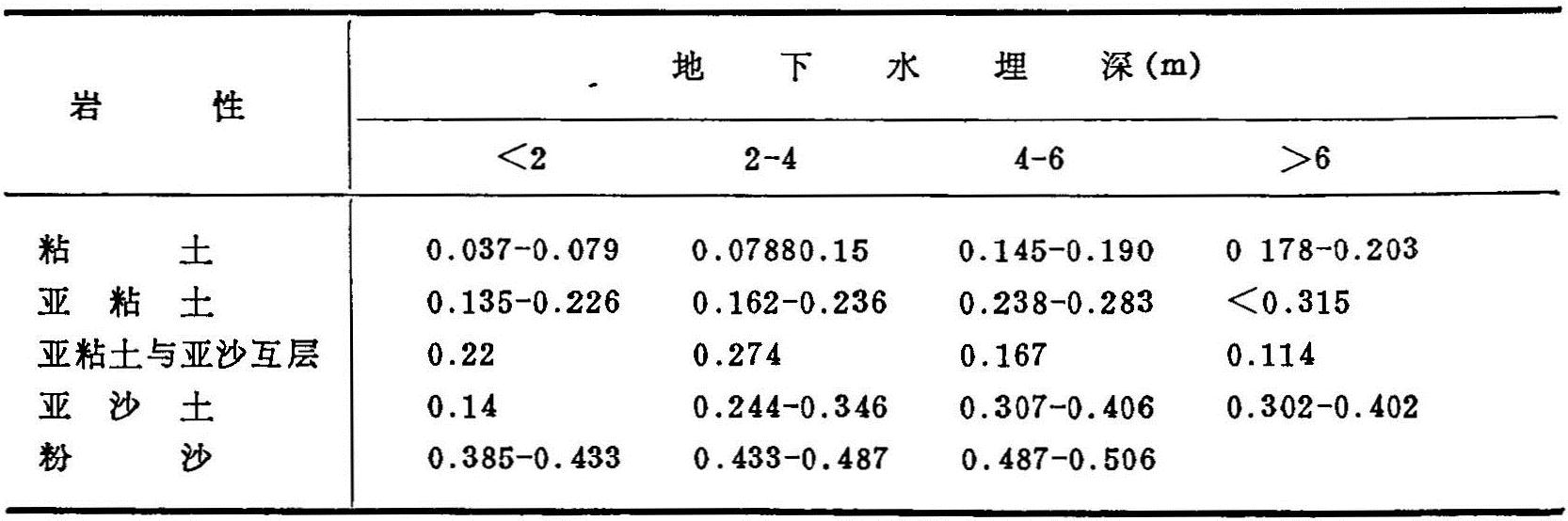
降水入渗补给量(QP):采用QP=a·P(P>15毫米),即假定降雨量>15毫米才产生入渗补给,a值参见表5.17。
灌溉回归量(QI):采用QI=β·I,β值取粘质土为0.07,壤质土为0.13,壤粘互层为0.12,沙质土为0.33。
表5.16 不同ASI、Wa及ETm条件下的月平均ETa1(mmd-1)
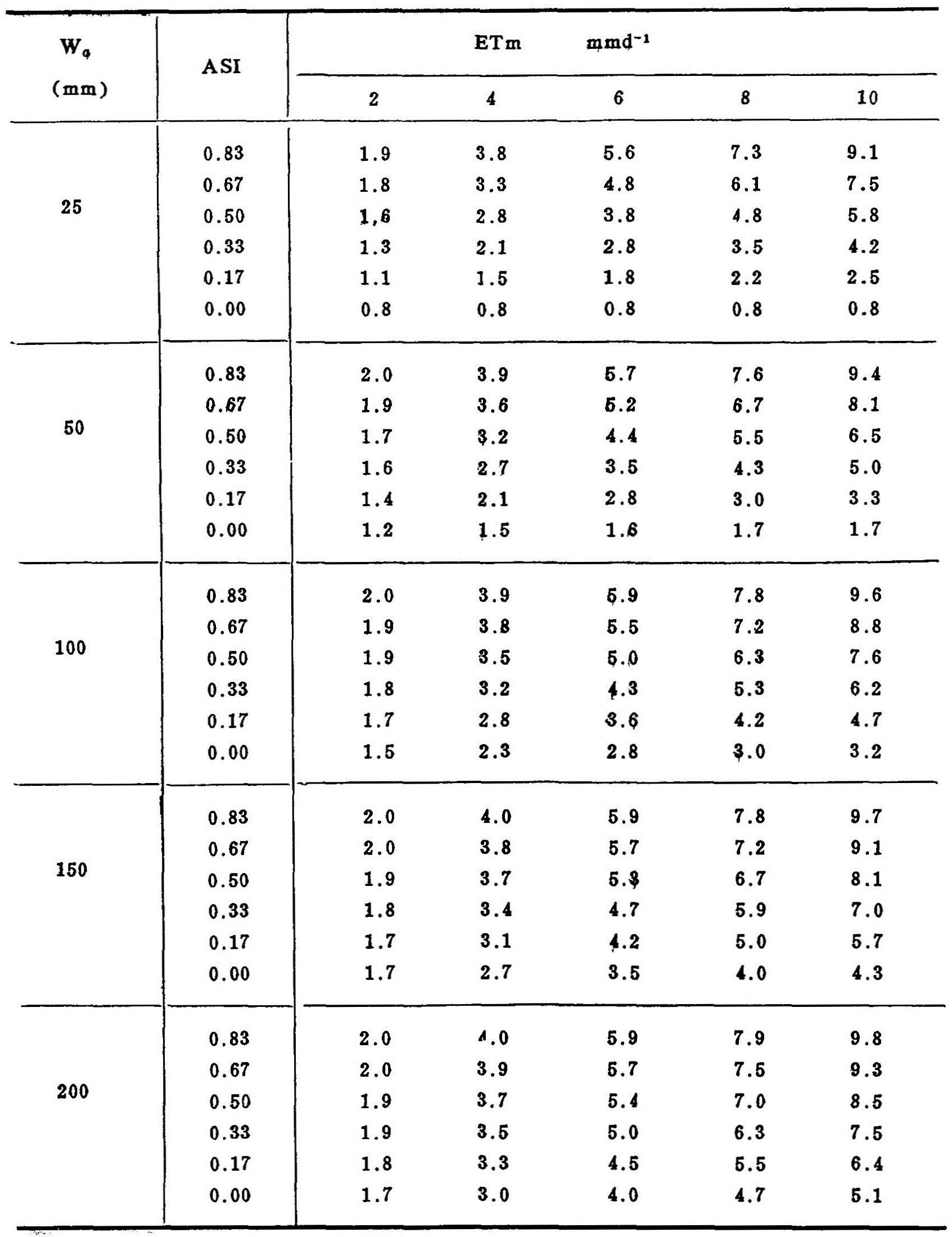
引自 Doorenbos et.al.1977重新整理
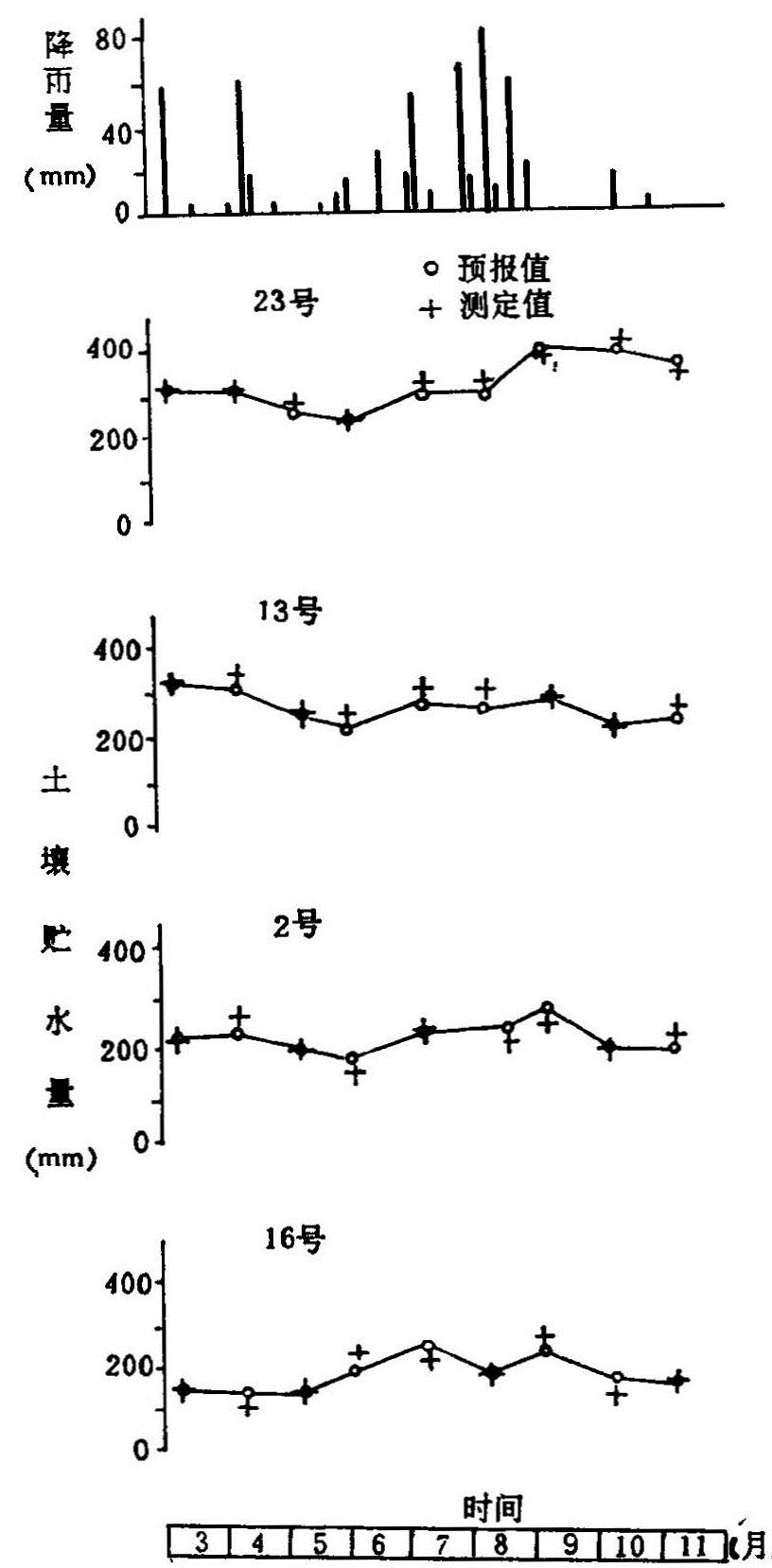
图5.8 农田土壤贮水量(0—100cm)预报值与测定值的比较
地面径流量(R):R=P-80,即当P>80毫米时才产生径流。
通过100厘米土层下边界的向上通量,用刘昌明等(1985)提出的地下水毛管上升量,WG(mm)计算式为:WG=(A-BlogH)·t/τ。H为地下水埋深;τ为作物全生育期的天数(小麦从拔节开始计算);t为计算时的生育天数;A、B为有关参数,依作物及土壤质地而异。
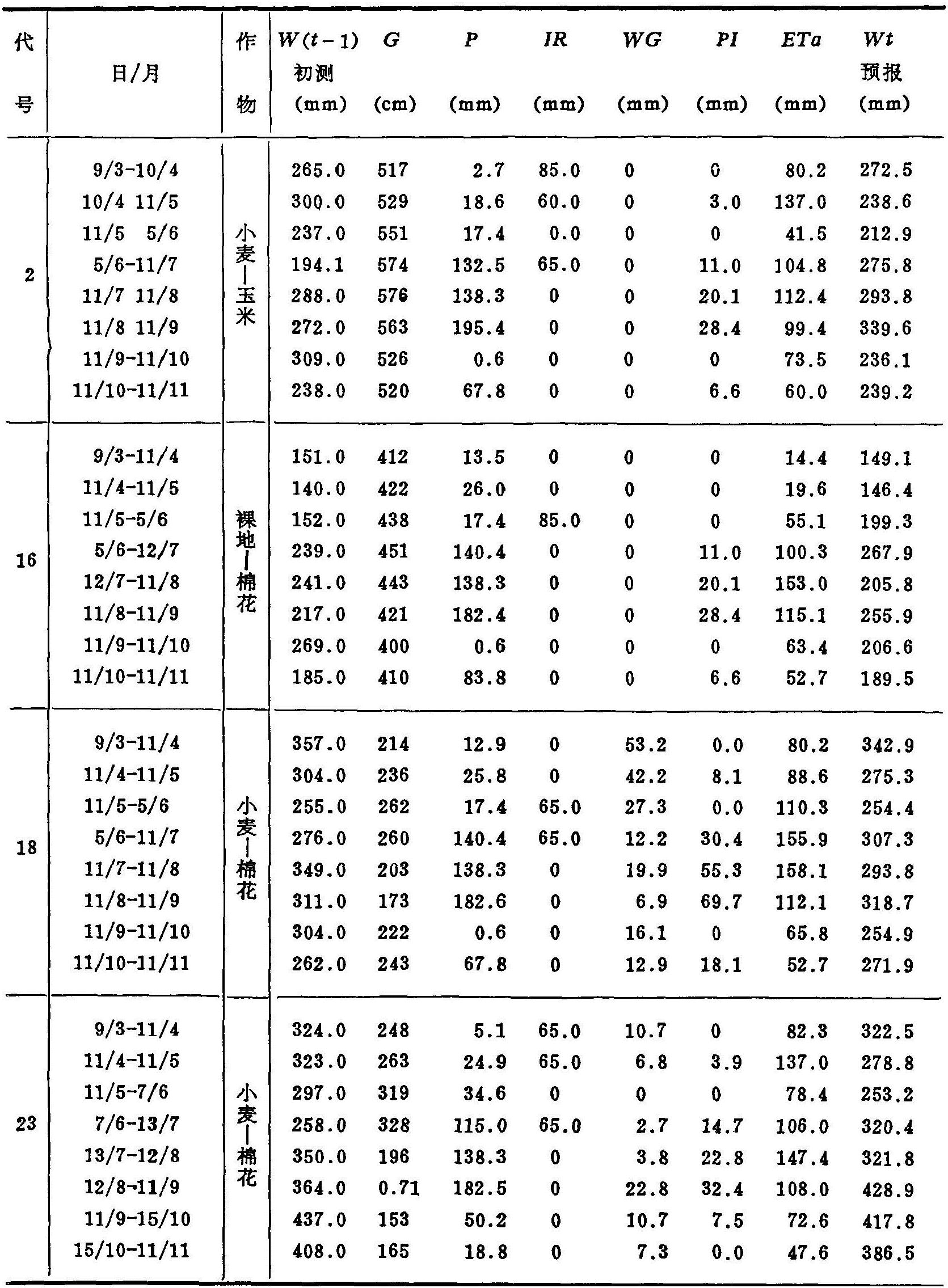
(3)农田土壤水量均衡预报:根据水量均衡模型,编写计算机程序,计算出时段末的土壤贮水量Wt。几个主要地学类型点的水量均衡结果见表5.18。表中上一时段末0—100厘米土层贮水量的预报值,即为预报下一时段的初始值,计算的上一时段末的预报值与下一时段初的实测值有较好的一致。图5.8表明各均衡分量的预报与估算可靠。分析不同地学条件下的农田水均衡状况,在微倾平原上部地下水埋深大(2号),麦田的蒸散耗水主要靠灌溉补充。而微倾平原下部地下水埋深浅(18号),麦田的蒸散耗水可以靠地下水补给。
表5.18 农田土壤水量均衡的预报及各个分量(mm)(1987)
(4)农田土壤水周年动态的预报
①土壤水量预报模型选用(5.5.4)式。
②预报分量及有关参数:
降雨量(P):用农田附近雨量站的实测资料。(从略)
灌溉量(IR):根据各种植作物的灌水计划量给出。
蒸散量(ETa):ETa=Ks·Kc·E0,E0值同表5.13。
根据不同时期的根系发育状况,将Kc按一定比例分配在i层(i=1—3,即0—10厘米,10—40厘米,及40—100厘米),分配比例见表5-19。
表5.19 Kc在1米土层中的分配
Ks的计算方法有三:
![]() (王季槐,1989;卢玉邦,1987)
(王季槐,1989;卢玉邦,1987)
Ks2=(Wt-W1)/(Wf-Wp)(刘昌明等,1988)
Ks3=Wt/0.7Wf(鹿洁忠,1982)
则 ETa2=Ks1·Kc·E0,ETa3=Ks2·Kc·E0,ETa4=Ks3·Kc·E0并令 Ks≥1时 ETa=ETm,Wt≤Wp时 ETa=0
渗漏量(Q):假定灌溉或降雨后,水分全部在当天末进入土壤,并假定当第一层的贮水量达到田间持水量后,若有剩余的水分方进入第二层,依次分三层下渗,当0—100厘米土层均达到田间持水量时,剩余的水量即为渗漏量,Q下,表达为:
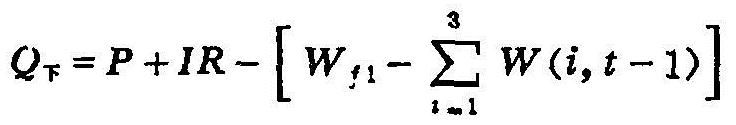
Wfl为1米土体的田间持水量(mm)
③农田土壤水周年动态预报
对8个地学条件土壤的1米贮水量进行逐日连续模拟计算,结果见图5.9。3条曲线分别代表ETa 3种取值方法的预报结果。
模拟值与实测值之间的平均相对误差为:方法一5.52%,方法二7.17%,方法三28.74%。1米土体贮水量(mm)的实测值y与预报值Xi的回归方程为:
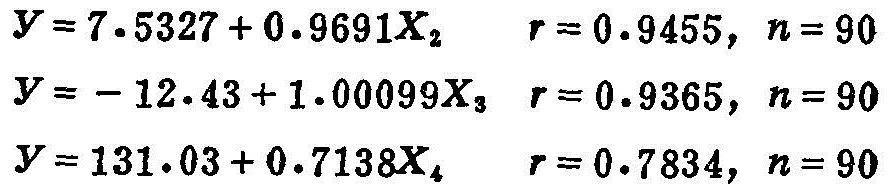
从图5.9看出:用ETa2与ETa3值预报的土壤水分贮量,较用ETa4值预报的土壤水分贮量与实测值接近,拟合率较高。从测定的农田土壤水分含量,可以求出相应的Wt/Wf(即Ks1值)及Wt/0.7Wf(即Ks3),在ETa的计算中,方法一假定当Wt=Wf时ETa=ETm,方法三假定当Wt≥0.7Wf时ETa=ETm,则从表5.2的数值可以看出不同土壤质地、不同栽培作物、不同地下水埋深的农田,当采用Wt≥0.7Wf的ETa=ETm时,全年除5、10月外,几乎ETa均等于ETm。由于计算的ETa值偏高,水量均衡的结果常使土壤的贮水量值偏低。
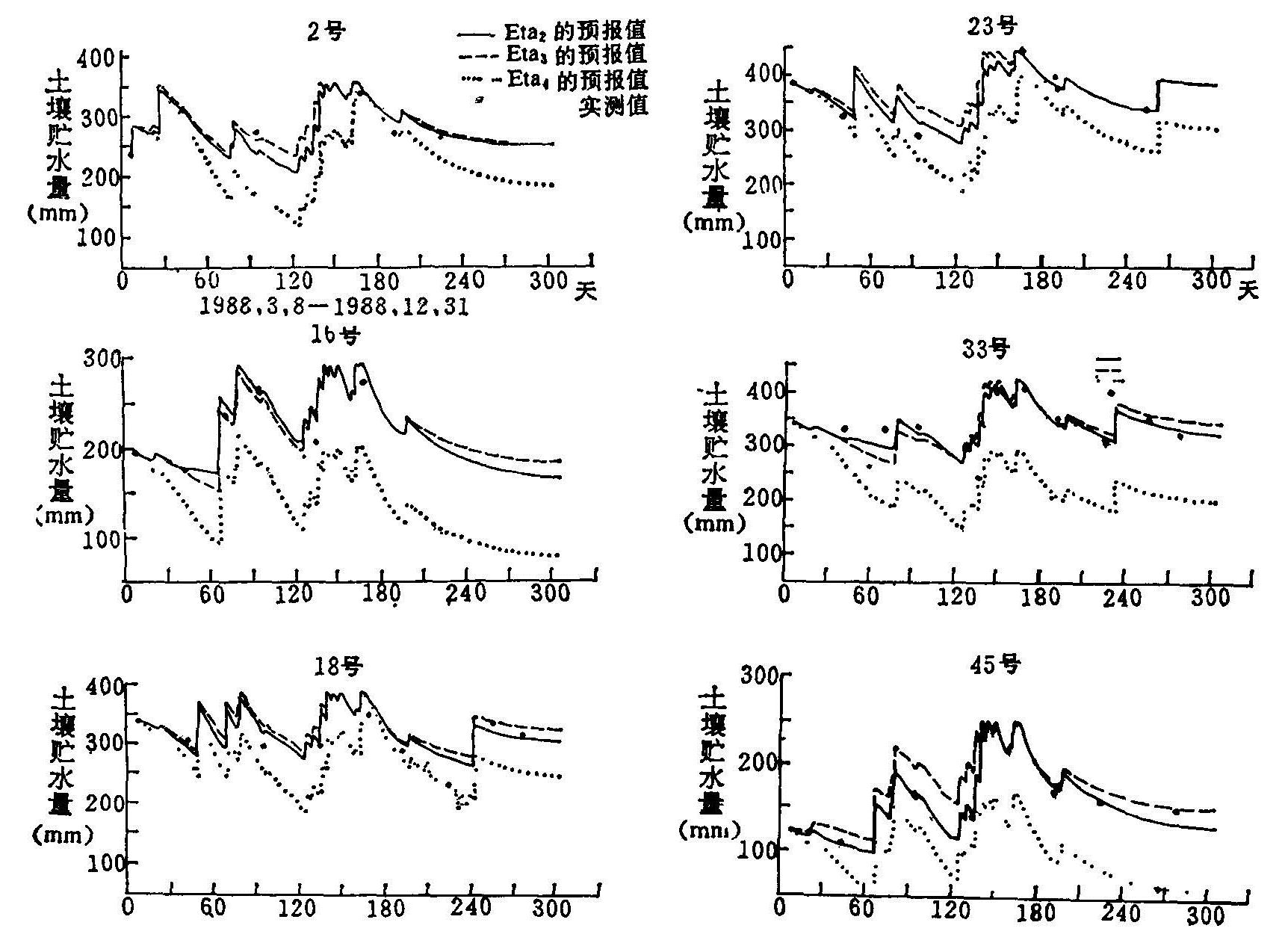
图5.9 几种农田土壤贮水量(0—100cm)预报值与测定值比较(1988)
Wt/Wf,即(Ks1)与(Wt—Wp)/(Wf-Wp),均可作为预报ETa的土壤水分系数。
从图5.9看出,各类农田在3—6月均为春季失墒期,7—9月为雨季增墒期,10—12月为秋冬缓慢失墒期。当地学条件和土壤类型不同时,失墒程度不同,因此栽培管理措施也应因地而异。