二、模型的实施
在得到(4.14)式以后,在一个地区对其具体实施,还涉及到许多复杂的问题,包括参数分区和参数确定;源汇项的具体区分及处理;边界条件的处理以及最终模型的运行与检验等。下面以曲周测报区Ⅰ区为例(背景条件见第三章),对区域地下水水位预报模型的实施作一较详细的论述。
在PWS体系中,对区域地下水水位(埋深)的预报,是针对整个区域水位的分布,所以单元的剖分要采用大小基本相等的单元。
考虑到模型的检验、调试模型与参数的方便性以及地下水观测孔的分布,在地下水观测井控制的范围内,剖分单元316个。有结点187个,其中内结点131个,边界结点56个。所有观测孔(57眼)都位于结点上,其中有26眼观测孔处在边界结点上。(见图4.1)
(一)参数分区及其参数确定
1.参数分区 由数学模型(4.3)至(4.10)式可知,需要确定的参数有K、μ、a、βk、c。而每一单元中这些参数都与地学综合体G有关,这就需要对这些参数在区域上进行分区。
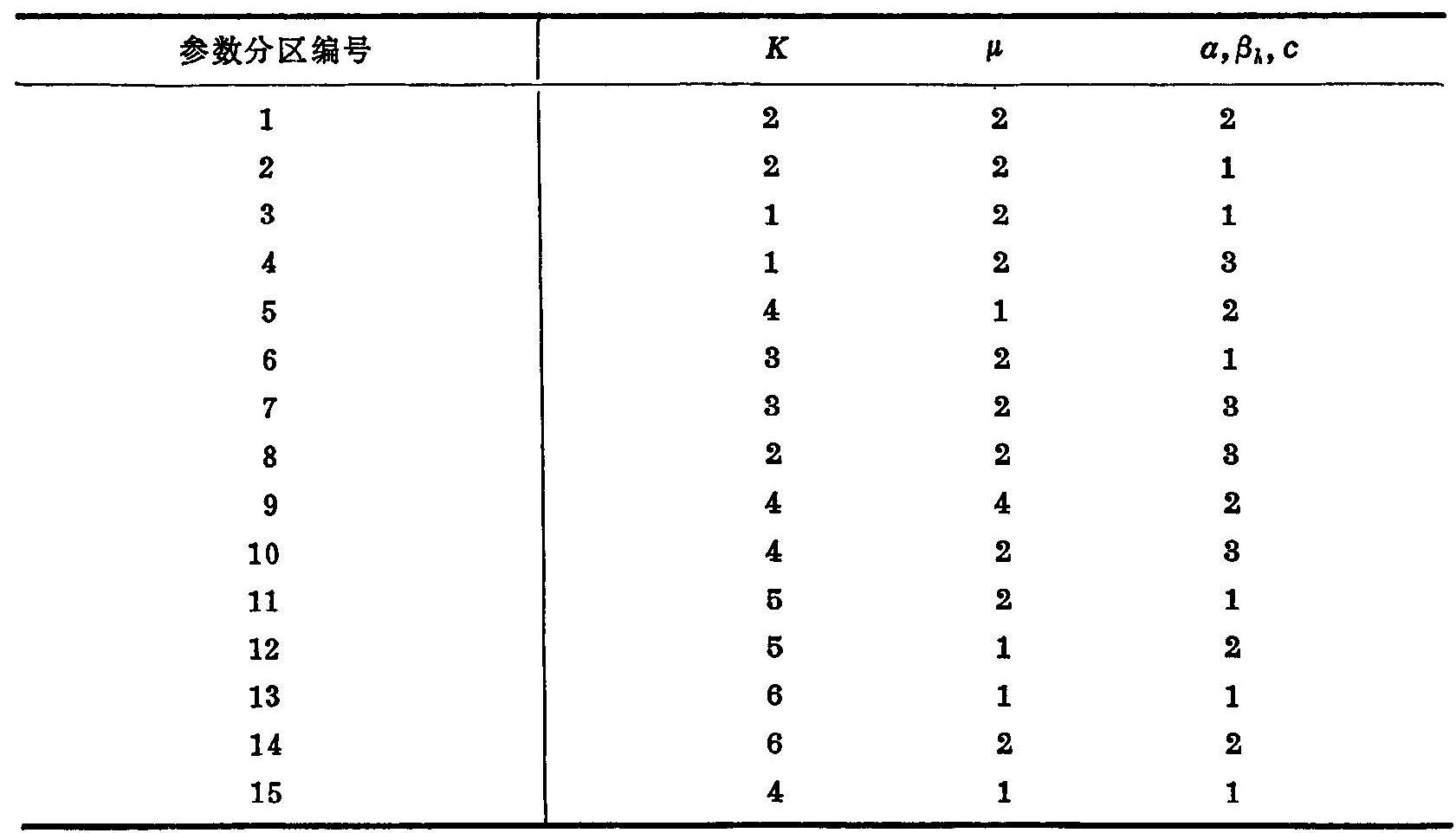
渗透系数K与浅层地下水的含水沙层特性有关。据本测报区水文地质图件、综合水文地质剖面图件等及其它相关图件,参数K划分为6个类型区。(见表4.2)
表4.2 K的分区所代表的水文地质类型

给水度μ的分区根据综合水文地质剖面图、土体构型图以及所观测到的地下水水位变幅资料,划分了两个类型区。(见表4.3)
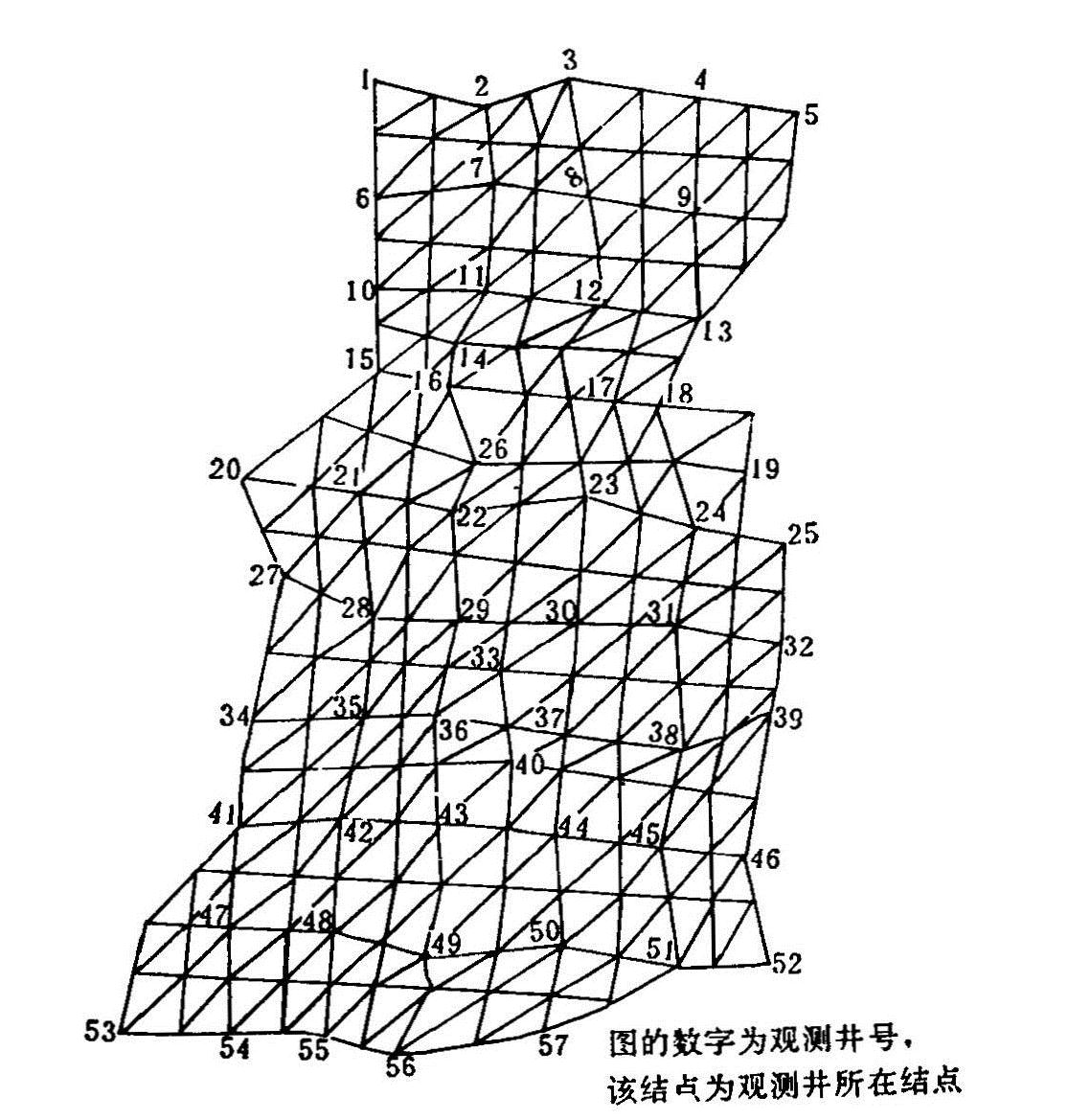
图4.1 测报区三角形单元剖分示意图
表4.3 μ的分区及所代表的类型

模型中垂直交换项Wg(x,y,t)中所选用的参数a、c、βk分区,根据土体构型划分了3种类型。(见表4.4)
表4.4 a、c、βk的分区及所代表的类型

把上面的三类参数分区图边界线进行概化,分别叠加到剖分的区域三角形单元上,最后得到综合参数的单元分区图。(见图4.2)共有15种类型区,每个区所代表类型见表4.5。
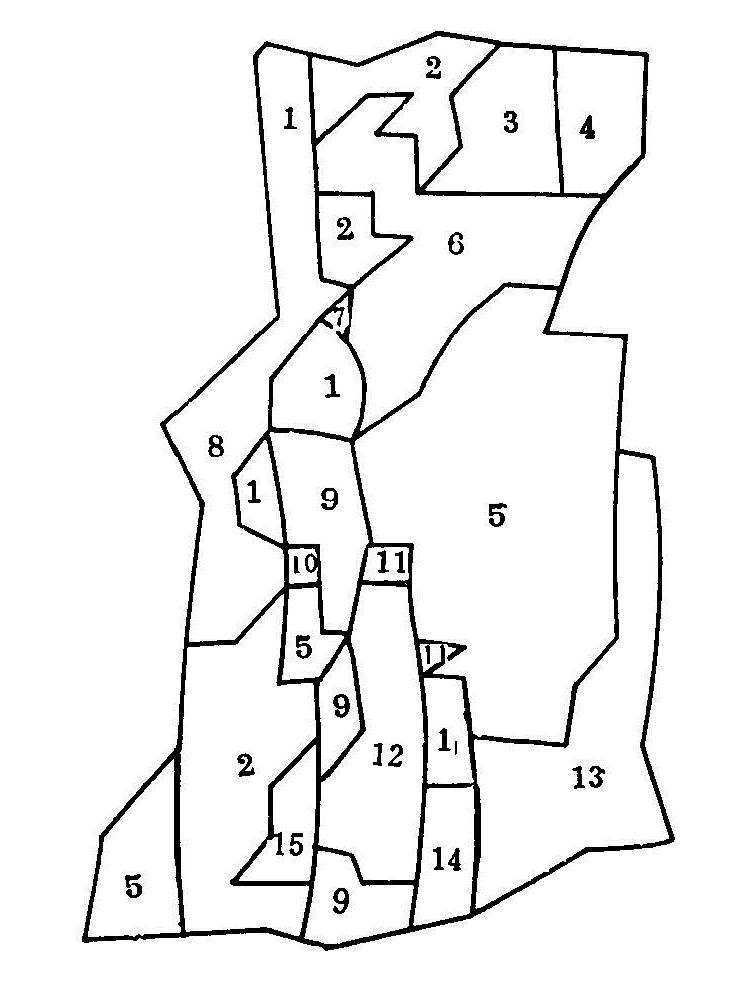
图4.2 综合参数分区图
表4.5 综合参数分区代号表
2.参数确定
(1)K的确定:对区域内各分区的渗透系数K,可通过选定典型点,进行抽水试验求出。此种方法工作量大,野外试验某些因素带有一定的随机性,所得结果很难被所建立的水动力学模型直接采用,但可作为模型的主要参考值或进行调试的初值。一般情形下,模型中选用的K值可通过下述方法求出:
①如本区内有抽水试验结果,可参照此结果给出每个分区的初始K值。
②选取区内一年内地下水水位稳定时期的观测资料(一般是每年1月至3月初),不考虑源汇项的作用(即(4.3)式中Wg(x,y,t)=0),解稳定流方程![]() 用单纯形优化方法对K值进行优化,得到中间结果。(关于单纯形优化法的算法可参照叶庆凯(1986)所著或其它有关优化算法的书籍。此方法在地下水动力学中的具体应用可参照薛禹群等,1980;张蔚榛,1983所著有关内容)
用单纯形优化方法对K值进行优化,得到中间结果。(关于单纯形优化法的算法可参照叶庆凯(1986)所著或其它有关优化算法的书籍。此方法在地下水动力学中的具体应用可参照薛禹群等,1980;张蔚榛,1983所著有关内容)
③选用一年完整的地下水水位观测数据,与其他参数(如μ,a,c,βk)一起,反复调试所建立的模型,最终确定模型实际运行所采用的K值。
选用1985年全区的地下水观测数据,参照河北地质大队邯邢中队在曲周所作的抽水试验结果(1978),曲周测报区I区6个分区所选用的K值见表4.6。
表4.6 K值优化及最终调试结果 单位(md-1)

(2)μ的确定:给水度μ的确定,可通过抽水试验、地下水长期观测资料拟合等方法求出。在黄淮海平原地区,水文地质工程地质研究所(1985)对此作了系统的研究与总结。参照此项工作所得每个类型区的μ值,结合曲周测报区所划分μ的类型,选定第一类型区μ1在0.08—0.16之间,第二类型区μ2在0.03—0.07之间。通过与其他参数的反复调试,确定:
μ1=0.09;μ2=0.054
(3)a、c、βk的确定:在每一个给定的区内,a、c、βk与地下水埋深d关系密切,而a、c、βk正如前述巳分析的那样,在冲积平原区,它们是影响模型预报准确度较灵敏的参数。而在PWS体系中,要求模型的预报准确度较高,所以,对其确定显得尤为重要。有关a、c、βk的确定方法,可参照水文地质工程地质研究所(1985)的研究成果。
在曲周测报区,a、c、βk的确定是依据李韵珠、陆锦文(1986)的研究成果,参照水文地质工程地质研究所在黄淮海平原所得的成果(1985),按照深度d=0,1,2,3,4,5,6(米)给出每个类型区的一组初值,利用1985年的实测地下水水位资料与气象(降雨、蒸发)、灌溉资料,与K、μ一起反复对模型(4.3)至(4.10)进行调试得到的。(见表4.7、4.8、4.9)
表4.7 a调试结果
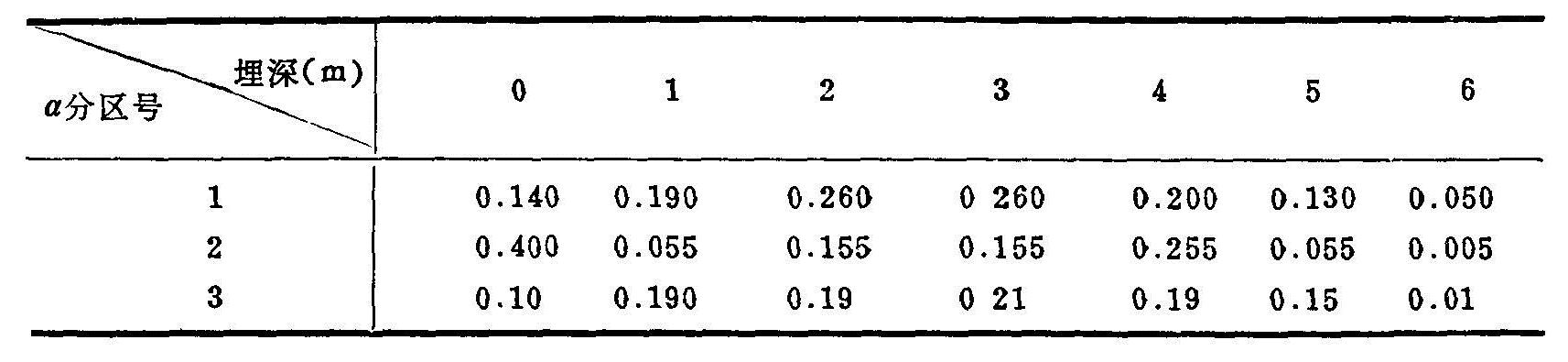
表4.8 c调试结果

表4.9 βk调试结果
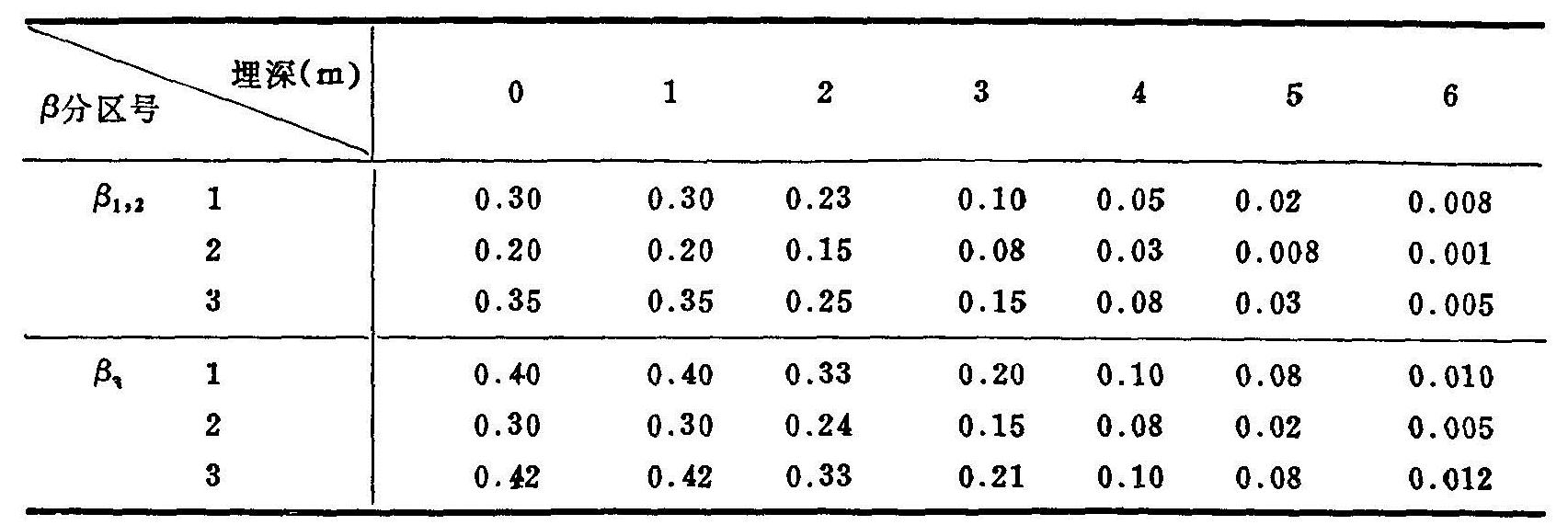
β1,2:深井、浅井灌溉补给系数;
β3:渠灌补给系数。
(二)模型中源汇项(Wg(x,y,t))的处理
1.降雨、蒸发子模型 已知a(x,y,d),c(x,y,d),输入逐日降雨量与自由水面蒸发量后,就可利用(4.8)和(4.9)式计算出每个单元的![]() 与
与![]()
具体过程如下:
对于i单元

式中 i:可反应空间(x,y)坐标;
τ:从t-1到t时段长。(https://www.daowen.com)
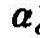 、
、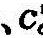 :地下水埋深为d时第i单元的a、c值。
:地下水埋深为d时第i单元的a、c值。
在模型运行时,所取时间步长为5天,考虑到次降雨量大小(王鹏文,1988)及滞后效应对![]() 修改如下:
修改如下:
处理降雨、蒸发子模型流程图见图4.3。
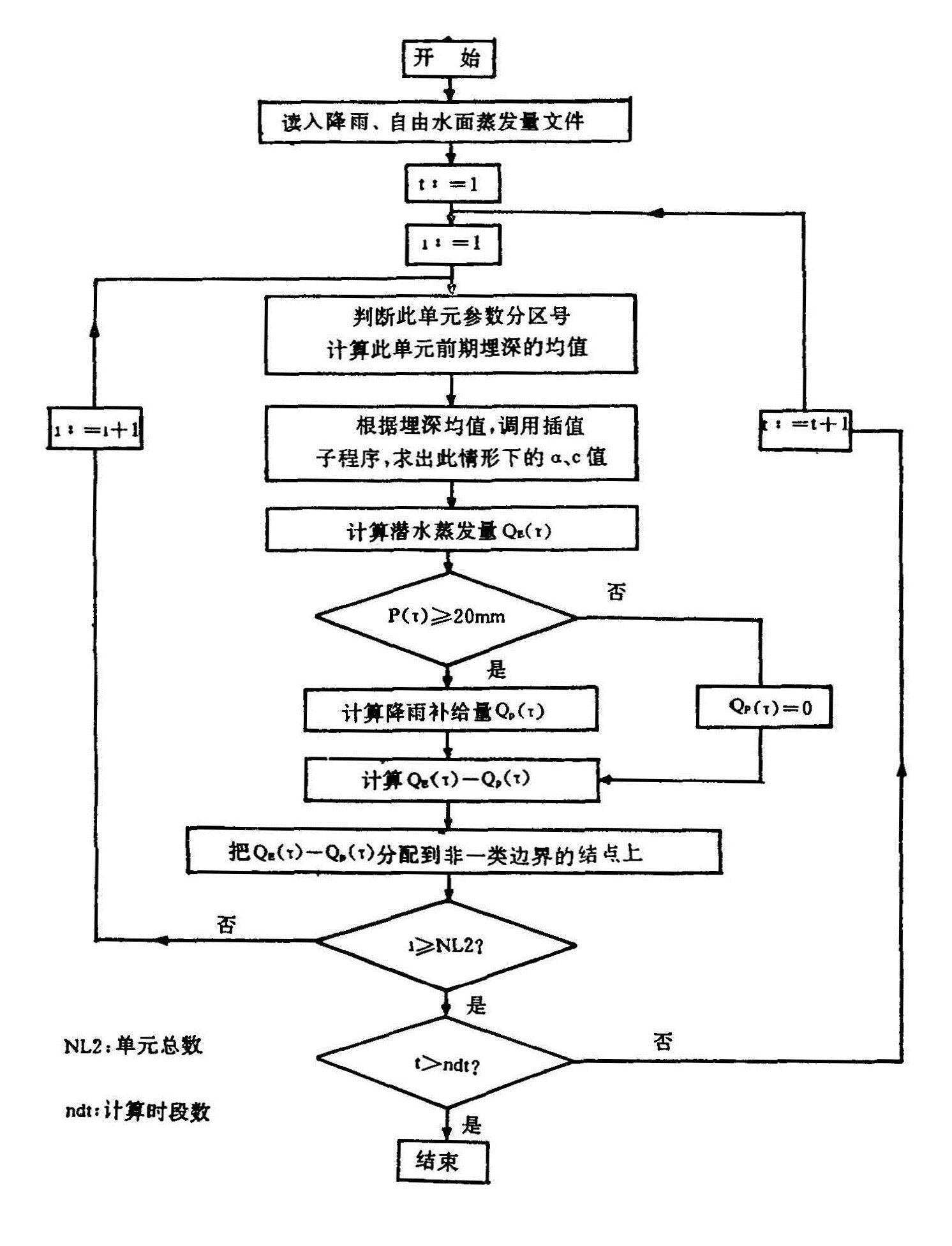
图4.3 处理浅层地下水的降雨补给、蒸发消耗子模型流程图
2.处理深井、浅井子模型 按照当地的种植制度,在一定的降雨年型下,考虑作物(小麦、玉米、棉花)需水规律,给出一灌溉识别矩阵。识别矩阵中行表示月份,列表示月份中划分的时段(5天为一个时段,每月共6个时段)。表4.10即为一灌溉识别矩阵。
表4.10 灌溉识别矩阵
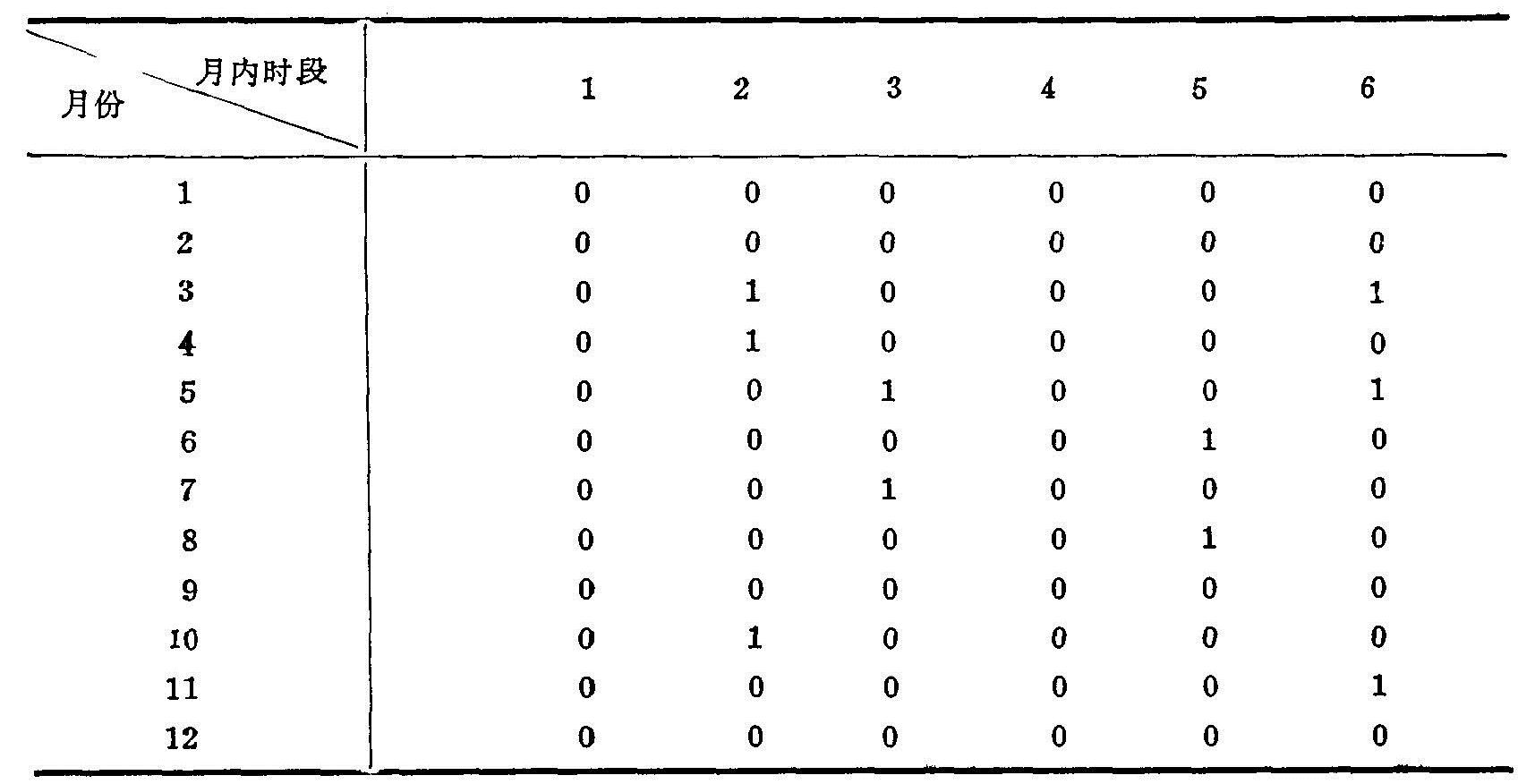
“0”表示不灌;“1”表示灌溉。
据灌溉识别矩阵即可确定出灌水期。给定浅井每小时抽水50-60立方米左右,深井70—80立方米左右,每天抽水6—10小时,这样据每个单元的深、浅井数目就可求出Qs及井灌补给地下水量。(见图4.4)井灌补给地下水量QI计算公式如下:
对于i单元
式中 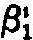 ,2,d:i单元、地下水埋深为d时,井灌补给地下水系数。
,2,d:i单元、地下水埋深为d时,井灌补给地下水系数。
3.处理渠系灌、补子模型 对于某一单元,当渠水位高于此单元地下水水位时,补给水量按此单元地下水水位每单位耕地面积补给1毫米计算,相反则地下水排泄量按每单位面积排泄1毫米计算,在河渠来水的情况下,还要通过灌溉识别矩阵判断是否抽取渠水灌溉,并且根据此单元的渠系灌溉系数(某一渠道可灌溉的面积占此单元内总灌溉面积的比例),与土地利用率推算出渠水的灌溉量。渠灌补给地下水量为:
式中![]() i单元地下水埋深为d时渠灌补给系数;
i单元地下水埋深为d时渠灌补给系数;
γi:i单元渠灌系数;
Li:i单元土地利用率(一般Li=0.8);
Ai:i单元面积(L2);
Irc(τ):τ时段灌溉定额(L)。
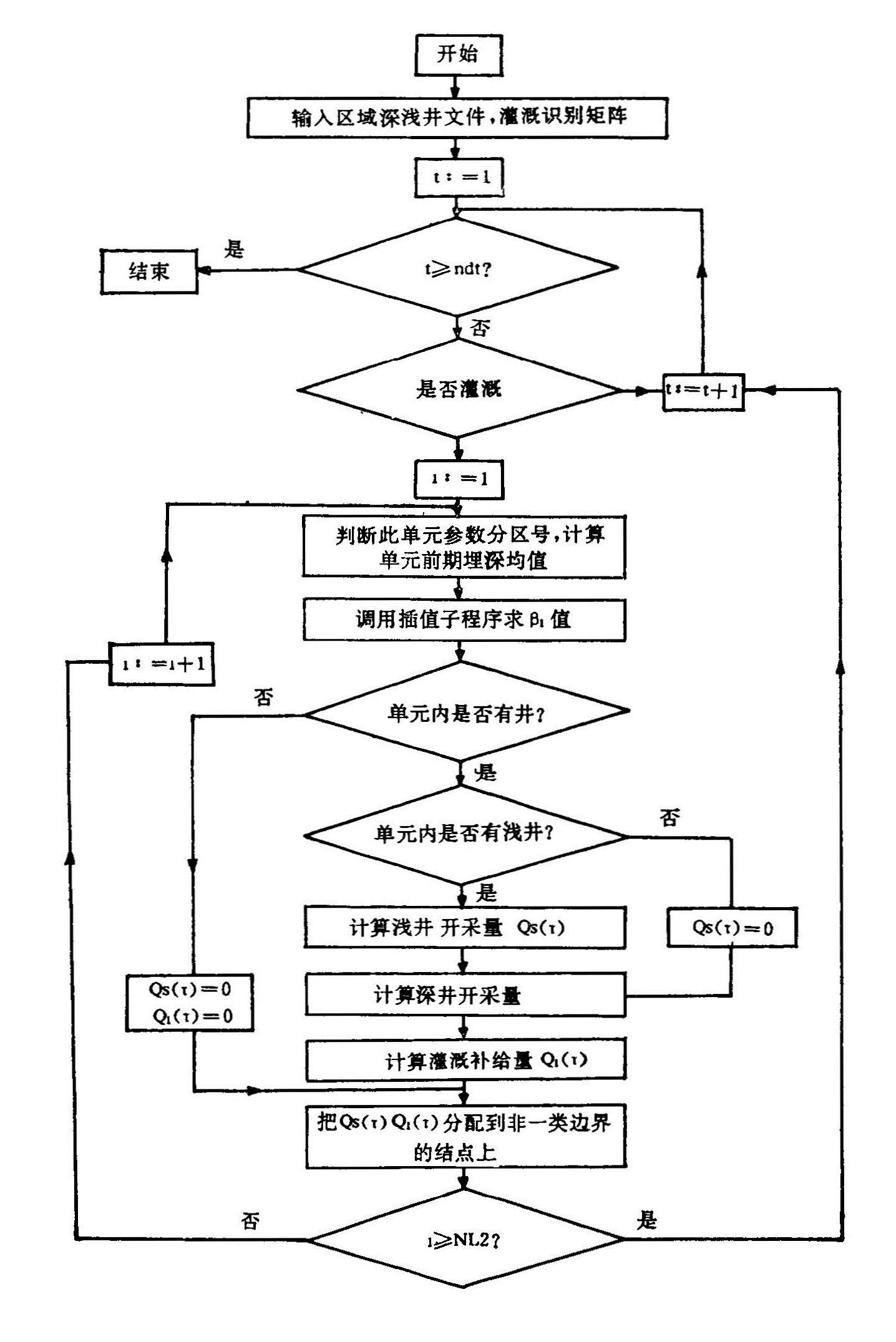
图4.4 处理深井、浅井子模型流程图
按照上述方法,对某一渠道沿其走向,依次一个单元接一个单元计算。在此过程中,某一河渠在某一单元流出的水量,等于上一单元的来水量与此单元内消耗与补给水量的代数和。对渠系处理子模型见图4.5。
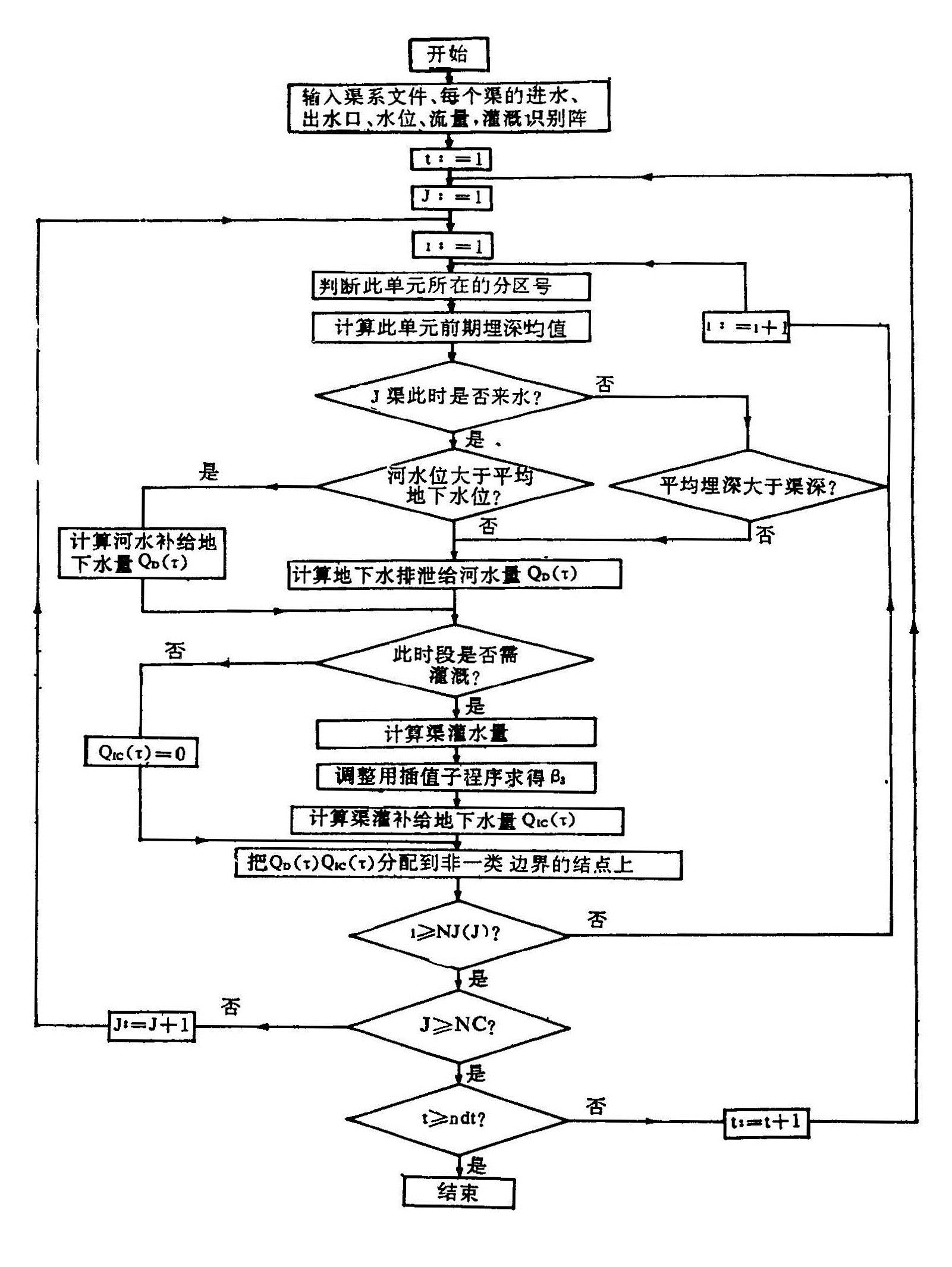
图4.5 处理渠系子模型流程图
NJ:渠道所经历的单元数;NC:渠道总数
(三)边界条件处理及模型的运行
在调试渗透系数初期采用第一类边界条件,其余情形下均采用第二类边界条件。有关边界条件处理的详细过程可参照有关文献(薛禹群,1980;孙讷正,1981;张蔚榛,1983)。
在边界条件确定后,模型就可上机运行。整体模型运行时输入的数据见表4.11,模型的运行过程见图4.6。
表4.11 模型所要求输入的数据

(四)模型的检验及应用
1.模型的检验 选用的时段为1985年3月至12月,计算值与观测值的拟合程度分3种类型。(见表4.12)类型1、类型2基本达到了模型的预报精度,也就是说模型的计算结果与实测数据的拟合率达86.8%。由此说明模型中所选用的参数基本可用。从53个观测井中选取4个具有代表性的观测点,给制出它们过程线比较图。(见图4.7)
从计算机自动给出的1985年6月、9月、12月实测等水线与模型计算出的等水位线来看,整个区域地下水水位的等值线分布状况基本相似。(图4.8(a)、(b))。
2.模型在季节性浅层地下水水位动态预报中的应用 时段为1987年上半年。按照模型输入的要求,输入1987年降雨、蒸发数据;1987年上半年地表来水很少,模型中暂不考虑;输入1987年的灌溉识别矩阵。参数选用及第二类边界条件的确定,均应用1985年资料模型调试的结果。用1月1日的观测水位作为初始条件,预报3月份的地下水位;用3月11日的实测水位作为初始条件,预报6月份地下水水位,运行模型,对结果分析如下:
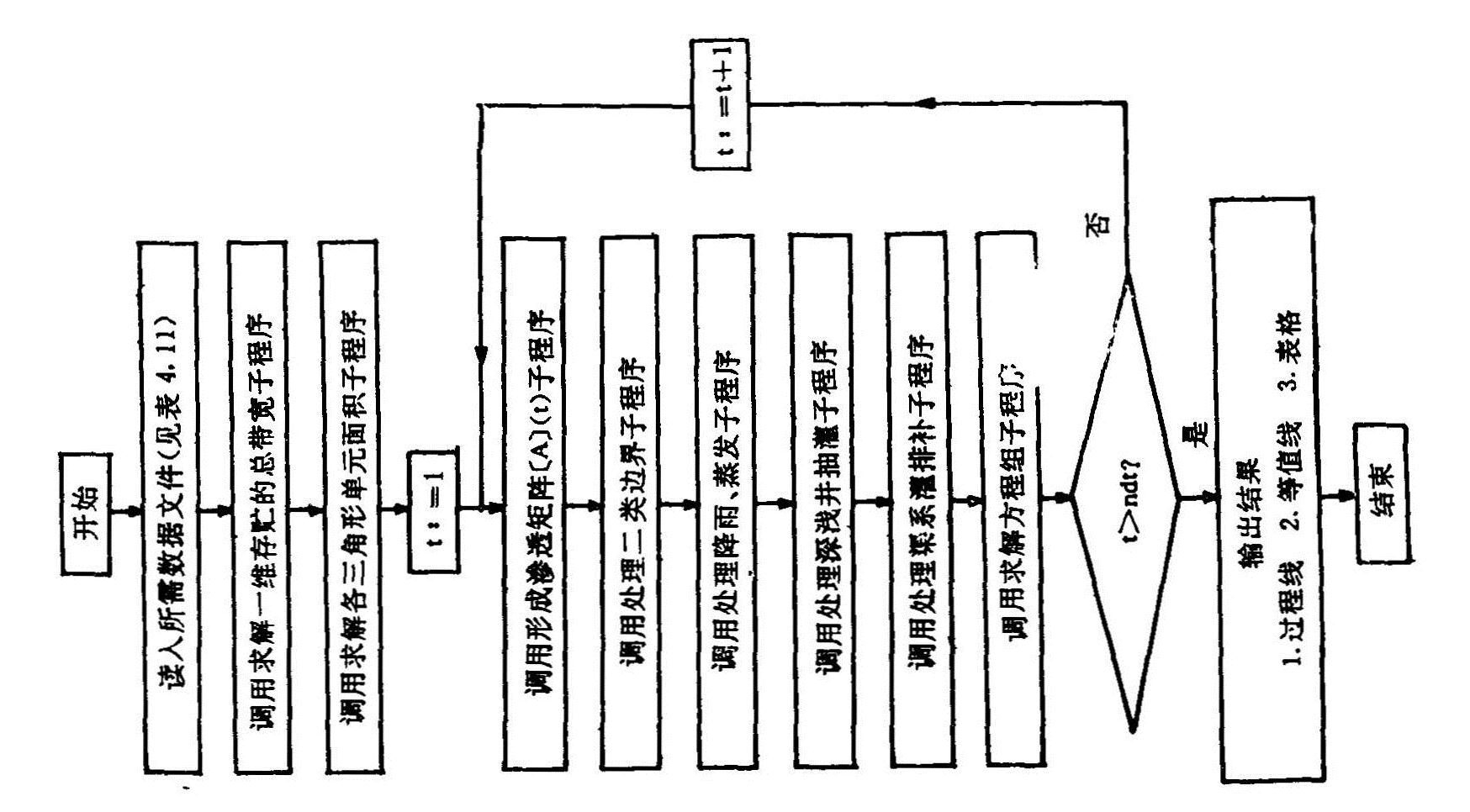
图4.6 地下水水位模型运行流程图
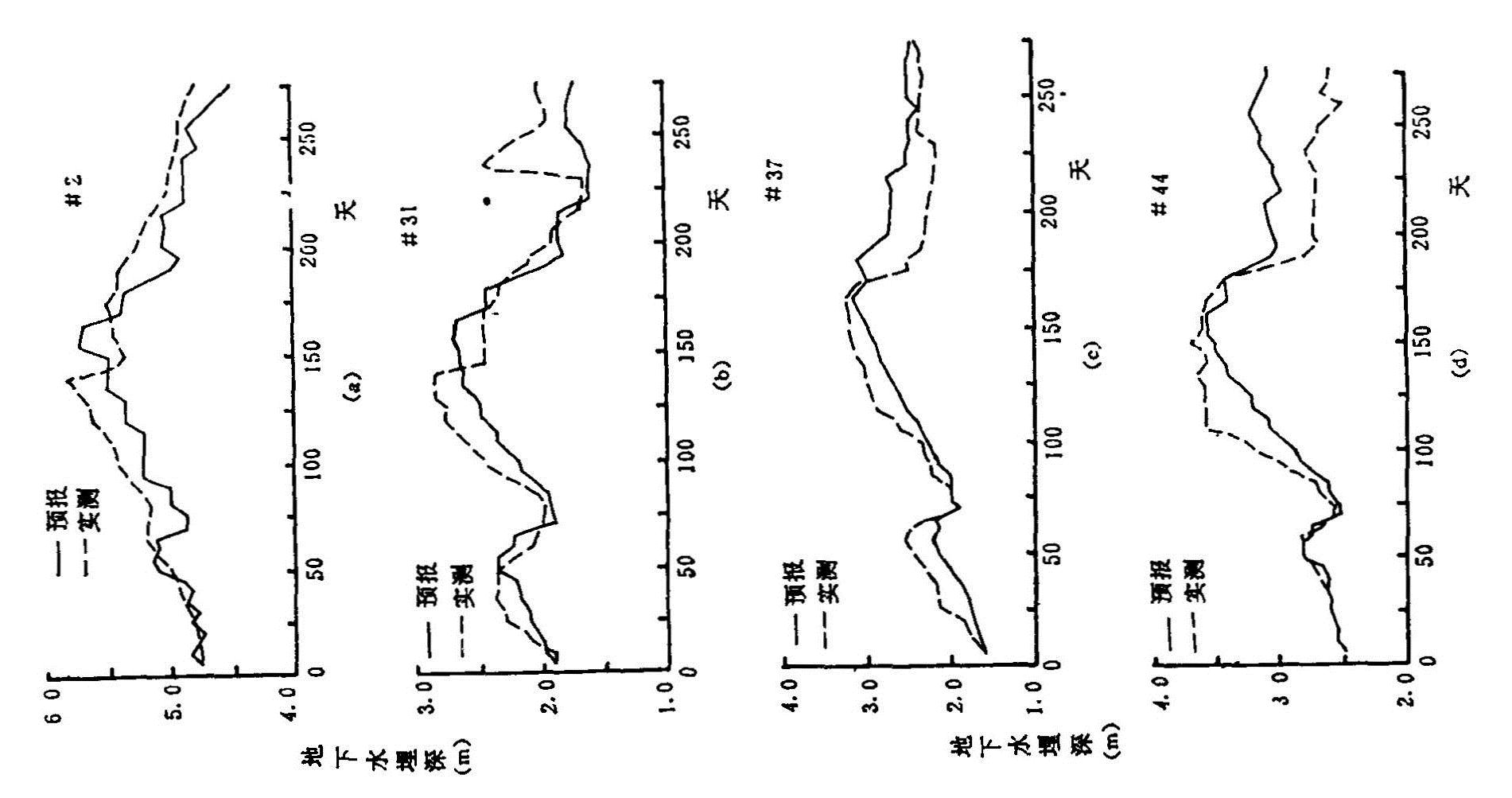
图4.7 地下水水位的实测与计算过程线对比
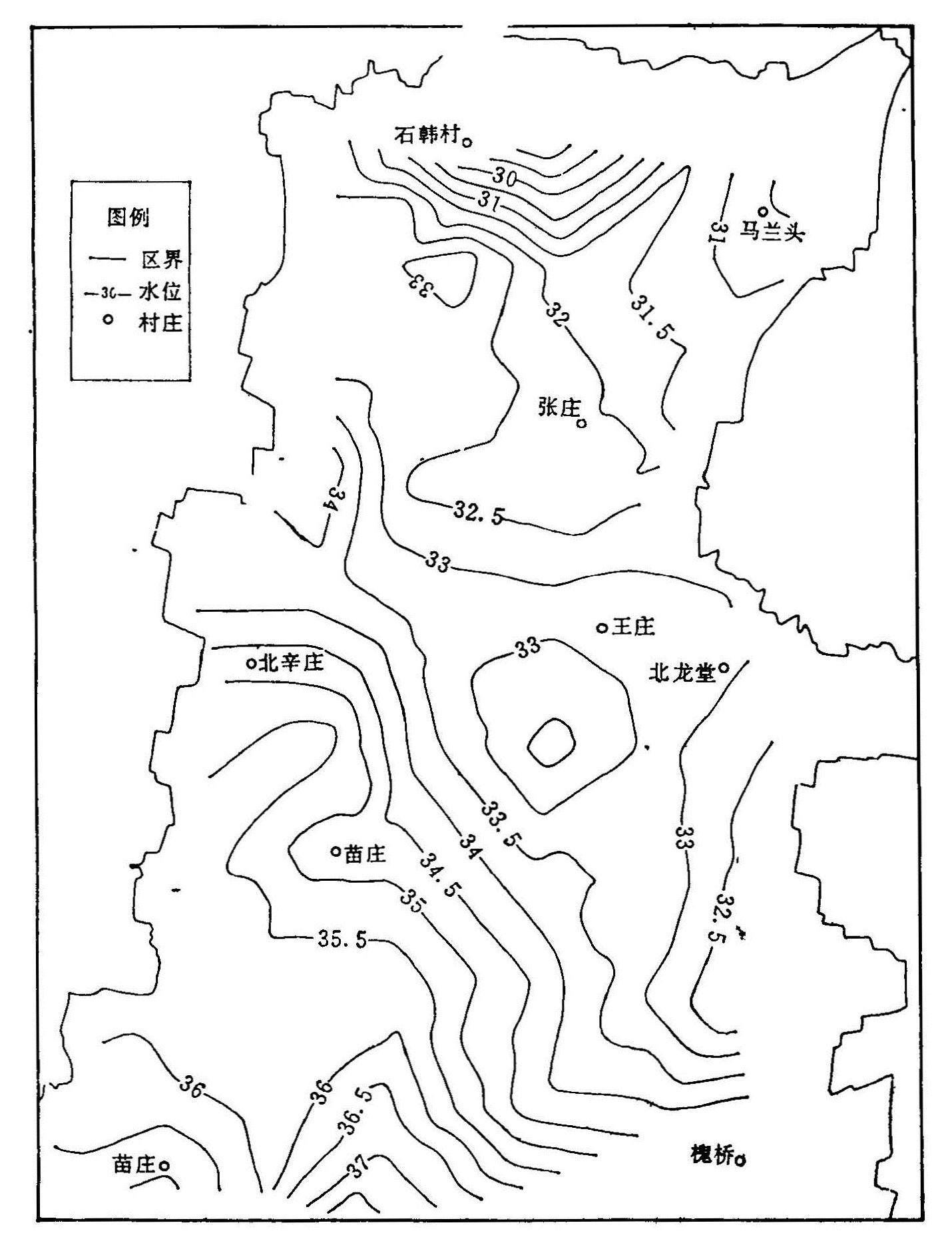
图4.8(a) 曲周测报区实测地下水水位(m)等值线图(1985.12.11)
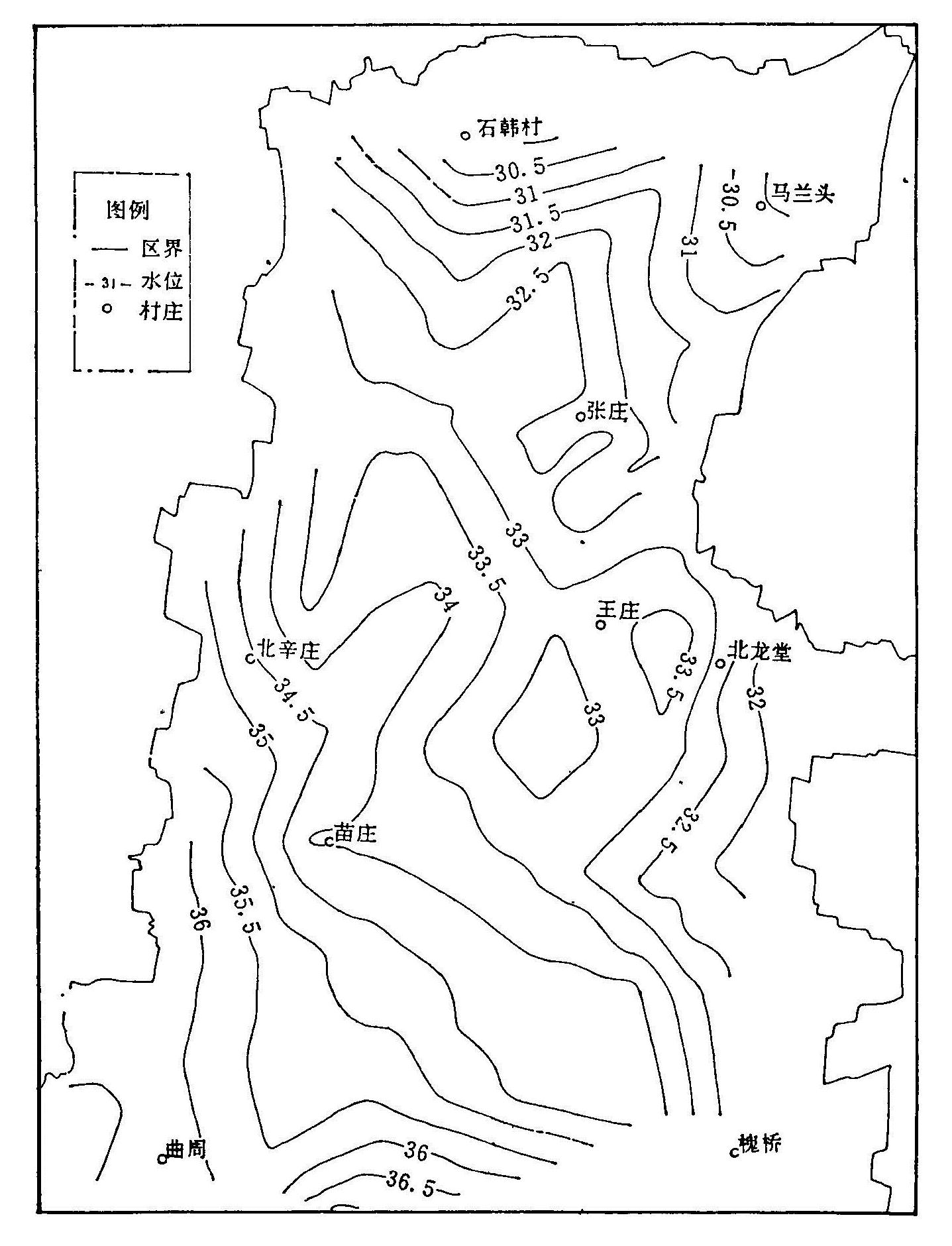
图4.8(b) 曲周测报区预报地下水水位(m)等值线图(1985.12.11)
表4.12 模型输出结果与实测数据对比

表4.13 1987年上半年预报值与实测值比较结果统计
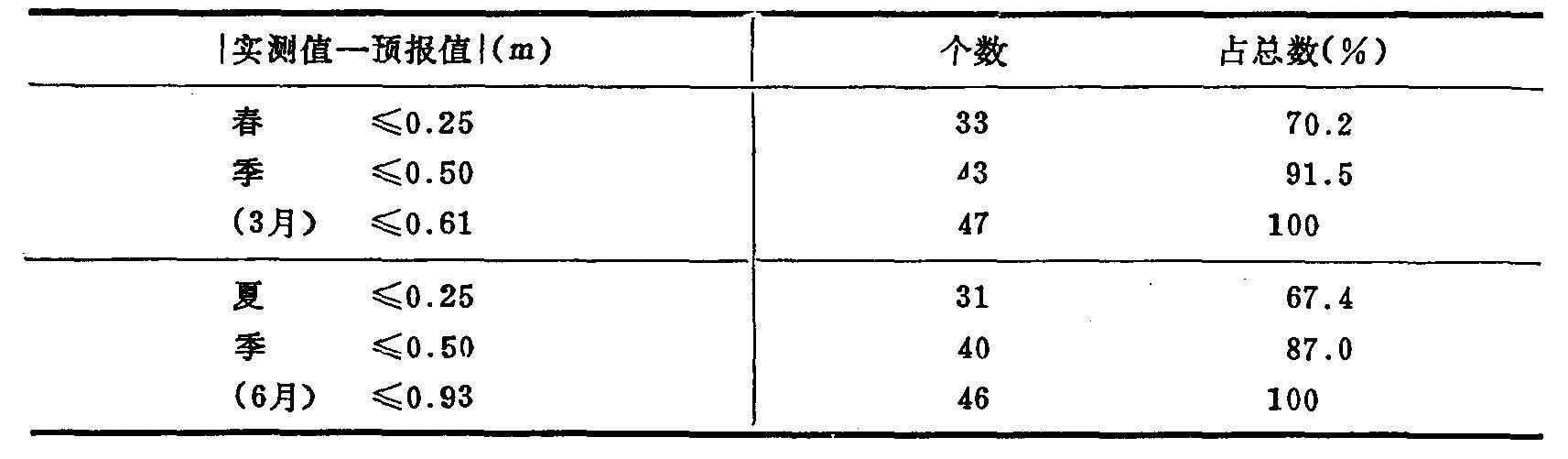
比较实测与预报的地下水水位等值线图,两者之间等值线的走向与趋势是相吻合的。为进一步检验其准确度,利用1987年各观测井实测值与预报值作比较分析。(见表4.13)如以≤0.25米定作区域水盐运动跨季度预报所要求误差的最低限度,则模型预报的准确率春季为70.2%,夏季为67.4%,基本达到了一般对浅层地下水水位进行季节性预报所要求的精度,可用于区域水盐运动管理中。
