区域土壤水均衡预报模型的建立
(一)区域集总式土壤水预报均衡模型
区域集总式土壤水均衡模型,采用集总式土壤水均衡分量及参数,或用全区各典型农田土壤水均衡要素的平均值进行预报,或在各典型农田预报的基础上进行预报值的平均所以各均衡要素的监测网点愈密,预报的精度将愈高。由于各均衡要素没有严格的空间边界,所以成图困难。研究区水均衡要素监测点的布局见图3.2或图5.10。本研究的区域集总式土壤水预报均衡要素,与农田土壤水预报均衡模型相同,预报模型采用(5.5.3)与(5.5.4)式。
(二)区域分布式土壤水预报均衡模型
区域分布式土壤水预报均衡模型中,土壤水均衡分量是通过分布式参数获得的。根据区域土壤水预报的概念模型,对区域土壤水状况依环境因子、内部各因子间的关系,特别是依其空间坐标分解为:
则整个区域D的土壤水分状况,据式(2.12)即为:
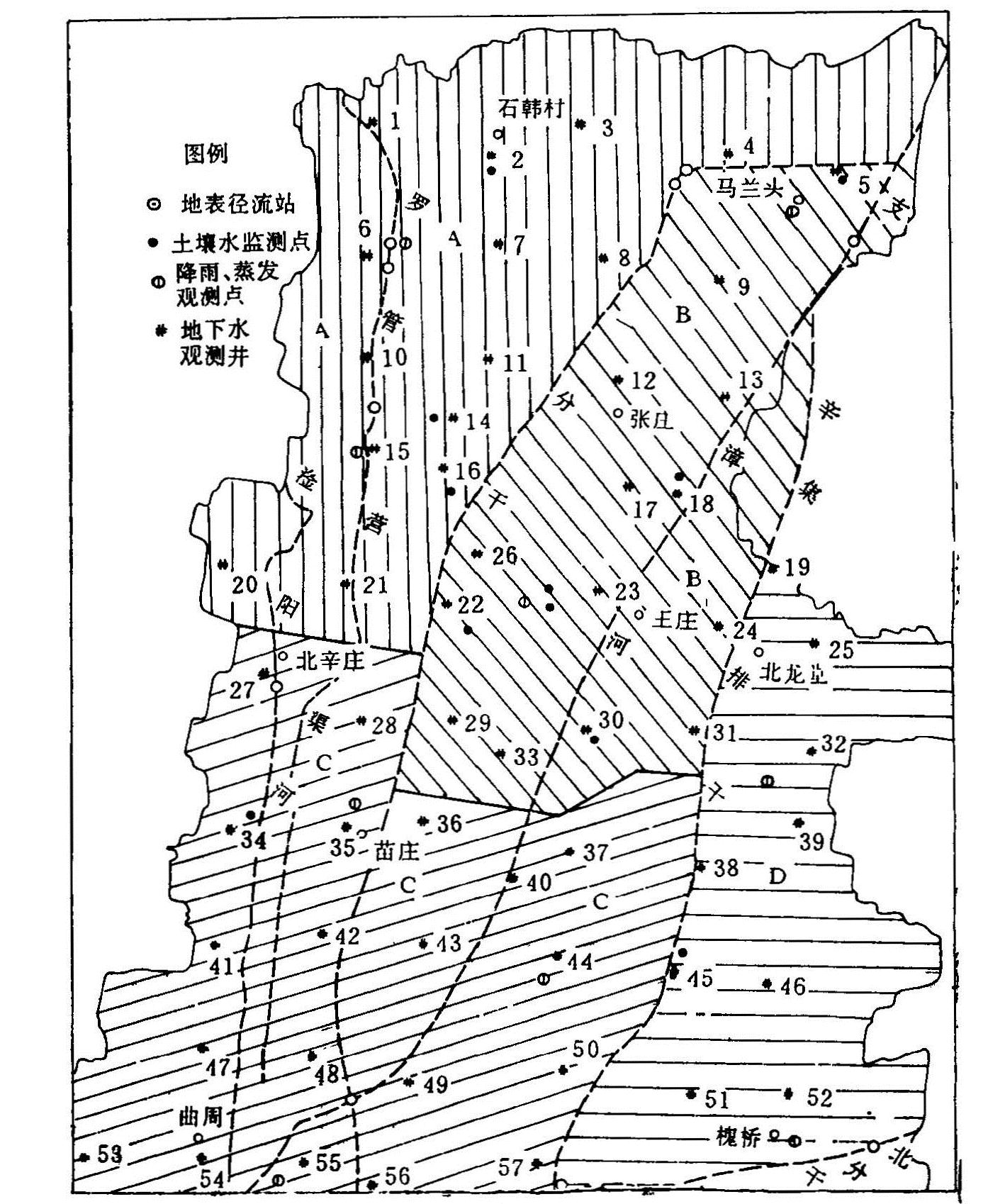
图5.10 曲周测报区水量均衡区的划分
RWSD3(t)={RWS(x,y)3(t)|(x,y)∈D}
式中 (x,y):空间上某一点的坐标(L);
RWS3:土壤水状况(L);
RWS1:地下水状况(L);
C3:气候因子对土壤水分状况的影响;
Ls:人为因子对土壤水分状况的影响;
G3:地学因子对土壤水分状况的影响;(https://www.daowen.com)
r13:地下水对土壤水的影响系数;
τ:为从时间(t-1)到(t)的时段。
对(2.25)式展开,则:
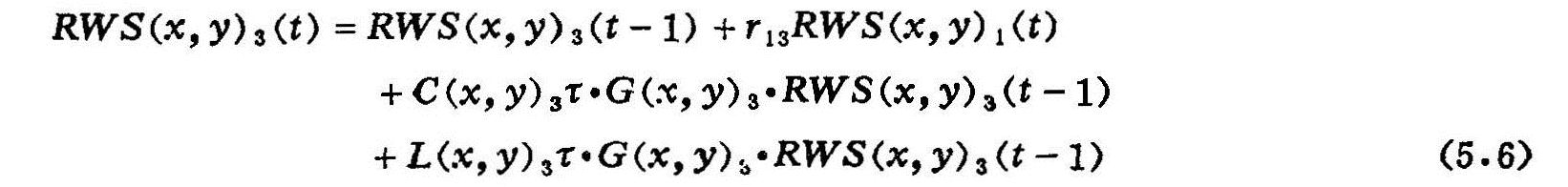
式中 RWS(x,y)3(t-1):时段初在(x,y)处的土壤水分状况;
r13RWS(x,y)1(t):(x,y)处土壤水与地下水的交换作用;
C(x,y)3τ·G(x,y)3·RWS(x,y)3(t-1):气候因素在前期土壤水分状况和地学因子的影响下,对土壤水分状况所起的作用;
L(x,y)3τ·G(x,y)3·RWS(x,y)3(t-1):在前期土壤水分状况和地学因子影响下人为因子,如灌溉、栽培措施等对土壤水分状况的影响。
为了求解上述概念性模型,必须把空间(x,y)引入传统的土壤水均衡方程,建立土壤水分布式的均衡模型,则区域分布式土壤水均衡模型可表达为:
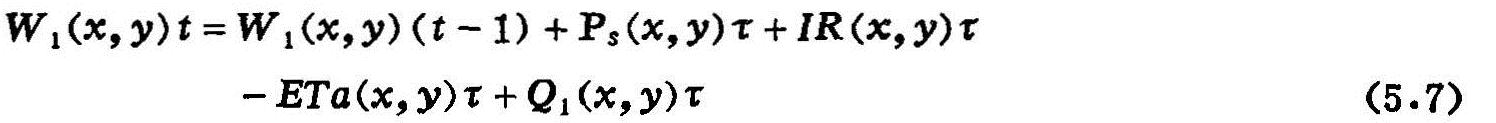
式中 W1(x,y)t:预报时刻t,(x,y)处1米土体的水分贮量(mm);
W1(x,y)(t-1):为时段初(t-1),(x,y)处1米土体的水分贮量(mm);
Ps(x,y)τ:时段τ内(x,y)处降雨量(mm);
IR(x,y)τ:时段τ内(x,y)处灌溉水量(mm);
ETa(x,y)τ:时段τ内(x,y)处通过1米土层蒸散的水量(mm);
Q1(x,y)τ:时段τ内(x,y)处1米土层下边界处,上下累计水分通量的代数和。
对于整个区域D在t时刻,1米土体的水分状况可表达为:
求解(5.7)式及(5.8)式,可对区域1米土体的土壤水分分布动态作出预报。
