有关分量及参数的确定
（一）区域集总式土壤水均衡模型的分量和参数
各分量及参数来源同5.2节，取值方法或直接用多点的平均值，或在各点分别预报的基础上，对区域土壤水状况进行预报。
（二）区域分布式土壤水均衡模型的分量和参数
在引入坐标（x，y）后，（5.2）式中的各项即可表达为W1（x，y）t、Ps（x，y）τ、ETa（x，y）τ、IR（x，y）τ……等。由于各分量的影响因素众多，从表（5.21）可知，各分项是其影响因素的函数，如Ps（x，y）是C、G、L的函数等。
各分量的确定方法如下（李保国，1990）：
1.Ps（x，y）的确定 Ps（x，y）τ为在（x，y）处τ时段内的降雨量，根据影响因素的分析，则：
由于G不随时间变化，所以在（x，y）处的Ps可简化为：
表5.21 分布均衡模型中各项的影响因子
RWS1：地下水水位；C、G、L分别表示气候、地学、人为因子。
在不考虑人为因素（L）对降雨的影响时，如不考虑作物的截留作用则（5.9.1）式可进一步简化为：
如假定在同一气候带，地貌类型一致的几百平方公里范围内平原区域降雨量无变化，则：
2.IR（x，y）的确定 IR（x，y）τ为在（x，y）处τ时段内的灌溉量，根据其影响因素的分析，则：
当W1（t-1）亏缺时，需通过灌溉满足作物需水要求，如忽略不同水分亏缺程度的影响，则可简化为：
则可在对G、L分区的基础上确定每一（x，y）处的IR值。
3.ETa（x，y）的确定 ETa（x，y）τ为在（x，y）处τ时段内的蒸散量，根据影响因素的分析，则：
式中E0及Kc的资料来源同前。根据（x，y）处的E0值及作物栽培情况给出Ks值，采用鹿洁忠（1985）的推荐式（苏联阿尔巴捷夫A·M），并对临界含水量值0.7Wf调整为0.8Wf，即：
其中
并令当W1（x，y）τ≥WT（x，y）时，Ks（x，y）τ=1
W1（x，y）τ≤Wp（x，y）时，Ks（x，y）τ=0
式中Wf（x，y）τ：1米土体的田间持水量；
WT（x，y）τ：1米土体的临界含水量；
W1（x，y）τ：1米土体时段τ内的平均贮水量；
Wp（x，y）τ：1米土体的萎蔫含水量。
4.Q1（x，y）τ的确定 Q1（x，y）τ为在（x，y）处τ时段内，1米土体下边界处水分通量的变化量，根据影响因素的分析，则：
式中 QE1（x，y）τ：τ时段内，（x，y）处通过1米土体下边界处向上的水分累计通量（mm）；
（QI1（x，y）τ+Qp1（x，y）τ）：τ时段内，在（x，y）处由于灌溉或降雨入渗，通过1米土体下边界处向下的水分累计通量（mm）。
如果假定地下水埋深不大于4米时，1米土体下边界处的水分通量变化，可分别由浅层地下水的蒸发量、降雨入渗补给量和灌溉回归量代替，则：
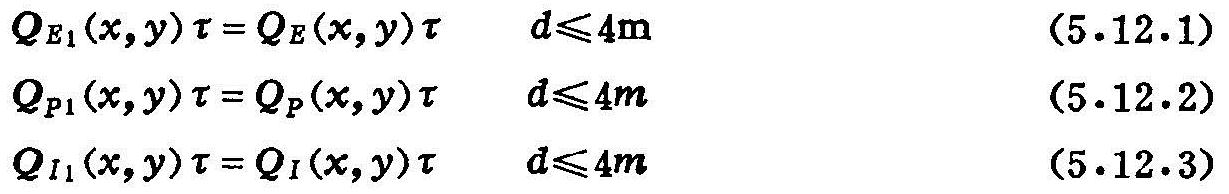
如地下水埋深＞4米，则可参考李韵珠（1988）或5.2节有关方法确定。（5.12.1）式至（5.12.3）式中，QE（x，y）τ、QP（x，y）τ与QI（x，y）τ分别与（4.16）式中
、（4.15）式中
、（4.18）式中
相当。