田间土壤多离子运移模型(AMDL)
田间土壤中盐分的一维运移,较土柱试验更为复杂一是土壤的不均一性,包括土壤层次的垂直变化和土壤盐分组成的不同;二是离子间和离子与土壤介质间的多种化学反应,常常使土壤盐分运动的准确模拟难以实现。目前,国外在模拟土壤溶质运动中,常常将可能发生的变化及相互作用尽量考虑进去,力求完善,但国内外大多数研究者,在要求预报精度不高的前提下,往往为了简化模型而省略了交换吸附和源汇项过程,和忽略了离子组成不同而引起的扩散弥散系数的差异。
这里介绍的田间多离子运移模型(AMDL),不仅考虑了在非饱和土壤中盐分运移时的交换、源汇等作用,也考虑了不同盐分的离子组成对扩散弥散系数的影响,同时又使模型尽量简化。因此假定:
①土壤阳离子代换量(CEC)保持不变;
②沉淀与溶解是土壤中重要的源汇因子,阳离子交换过程是瞬态平衡的;
③只考虑硫酸钙的沉淀与溶解作用。土壤溶液存在一个Ca2+与![]() 的溶度积Ksp,当两离子的活度积>Ksp时,出现沉淀,<Ksp则出现溶解(如此时存在固体CaSO4的话);
的溶度积Ksp,当两离子的活度积>Ksp时,出现沉淀,<Ksp则出现溶解(如此时存在固体CaSO4的话);
④CaSO4的比表面积不变;
⑤温度恒定。
⑥只考虑裸土和层状土壤,地下水水位可以变动。
在上述假设下,建立和检验一个适于田间土壤条件下的加和性模型,同时包括参数确定和估价源汇因子。
(一)模型的建立
如果土壤盐分运移中设有n种离子,那么这n种离子的综合运动就可以用下列方程来描述:
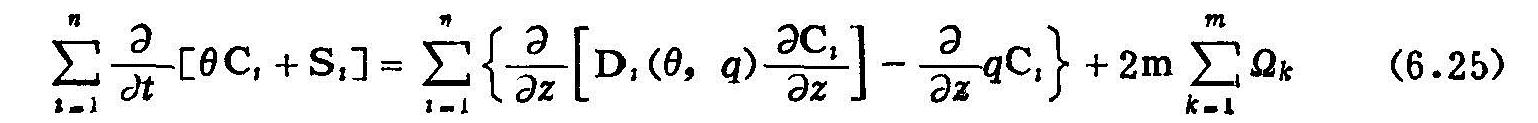
式中 下标i和k:分别代表离子和化合物;
m:表示化合物种类数;
θ:体积含水量(cm3cm-3);
C:土壤溶液浓度(moll-1(p+或e-));
S:交换态离子含量(mmolcm-3(p+));
D:盐分扩散弥散系数(cm2d-1);
Ω:CaSO4沉淀溶解速度(mmold-1cm-3),或其他化合物的源汇作用速率;
q:达西流速(cmd-1);
t:时间(d);
Z:土壤剖面深度,cm。
引进离子组成分数r,
令:![]() 和 r
和 r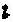 =C
=C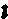 /C,
/C,
则有:C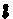 =r
=r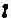 C 和
C 和![]()
将C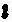 =r
=r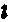 C代入式(6.25),整理得:
C代入式(6.25),整理得:
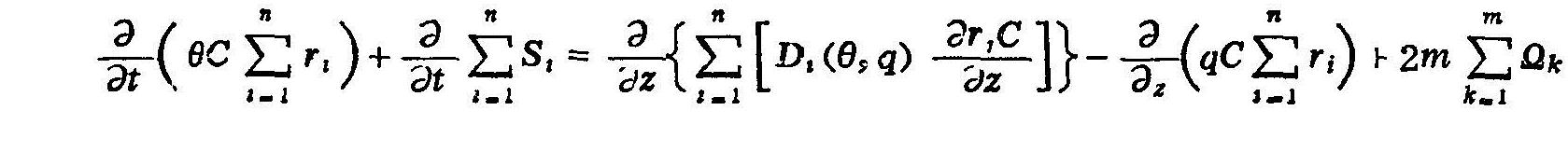
这里:![]()
所以:
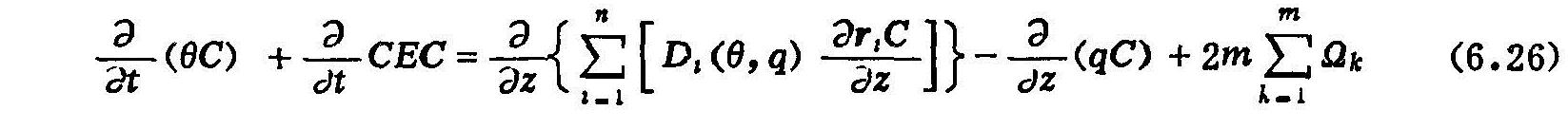
根据前面的假定,CEC不变,∂CEC/∂t=0,则(6.26)式进一步简化成:
对于一个给定的当地条件下长期发育的土壤来说,其土壤溶液中的离子组成在一个较短的时期内,可以看成是基本不变的。因此方程(6.27)中的r,对每种具体离子来说,可以粗略认为是常数,至少在某一时段、某一土层内如此,所以(6.27)式成为:
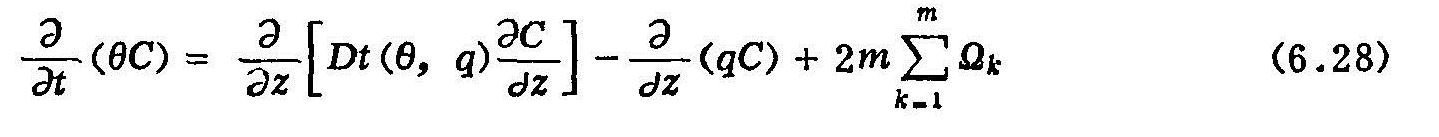
式中

称为多离子综合扩散弥散系数。
如果只考虑CaSO4的沉淀作用,则(6.28)式中的![]() 由一个二级反应方程,估计:
由一个二级反应方程,估计:
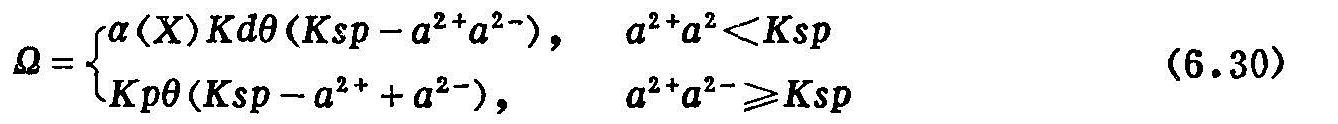
式中 Ksp:溶度积;
Kd、Kp:分别为溶解、沉淀的速度常数;
a2+和a2-:相应于Ca2+和![]() 的离子活度;
的离子活度;
X:土壤的固态CaSO4含量(mmolcm-3);
 (X):意义同前。
(X):意义同前。
方程(6.28)通过与下面的水流方程联立进行计算:
式中 h:基质势,cm水柱;
Cw:比水容量;
K(h):导水率(cmd-1)。
模型AMDL式(6.28)和(6.31)采用不等距有限差分法求解。
(二)参数确定
模型AMDL包含参数Dt、Kp、Kd和Ksp4个,此外离子组成分数r,亦是需要确定的重要常数之一。
(6.29)式也可写成:![]() 假定流速υ和含水量θ对各个离子的扩散弥散系数D
假定流速υ和含水量θ对各个离子的扩散弥散系数D 影响是相同的,若选用下式表达这种影响:
影响是相同的,若选用下式表达这种影响:
则意味着对各种不同离子,其λ和a、b都维持同一个常数。式中Do 为各个离子在自由水溶液中的扩散系数。这样:
为各个离子在自由水溶液中的扩散系数。这样:
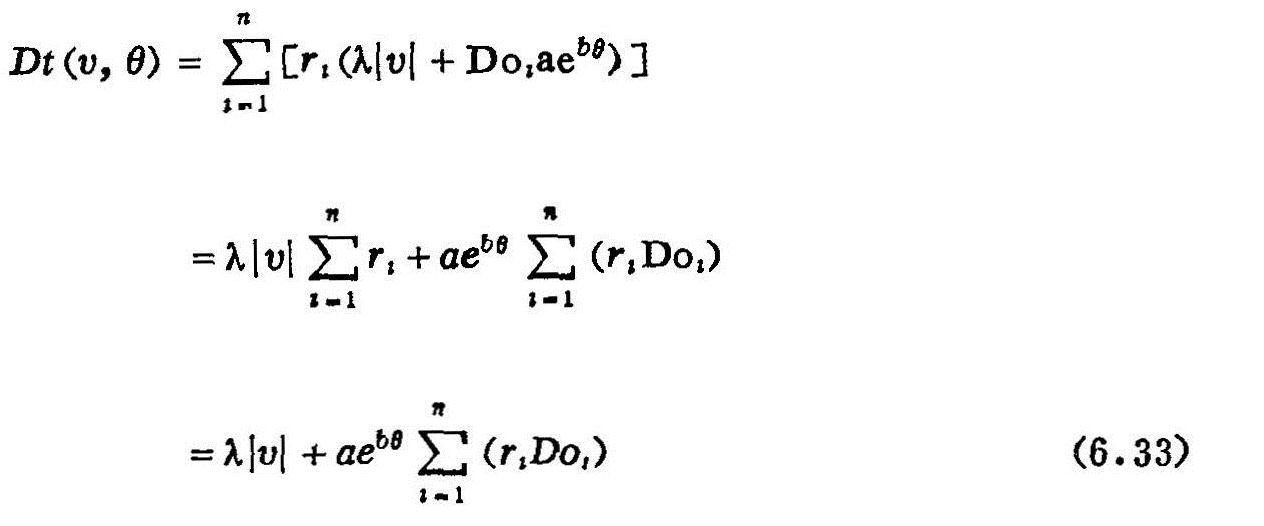
本文所考虑的离子Ca2+、Mg2+、Na+、SO42-和Cl-,各自的Do值引自Nye(1977)
λ、a和b的取值,经第一个观测月试算后选用:
λ=0.5,a=0.004,b=10.0。
化学反应常数Kd和Kp由前节给出:
Kp=192.0lmol-1d-1,Kd=8.161ml-1d-1
硫酸钙沉淀与溶解的溶度积Ksp的初始值,取25℃时的溶解积6.26×10-5(南京土壤所编《土壤理化分析》第23页)后,用第一个月的观测资料试算,结果为6.36× 10-5。
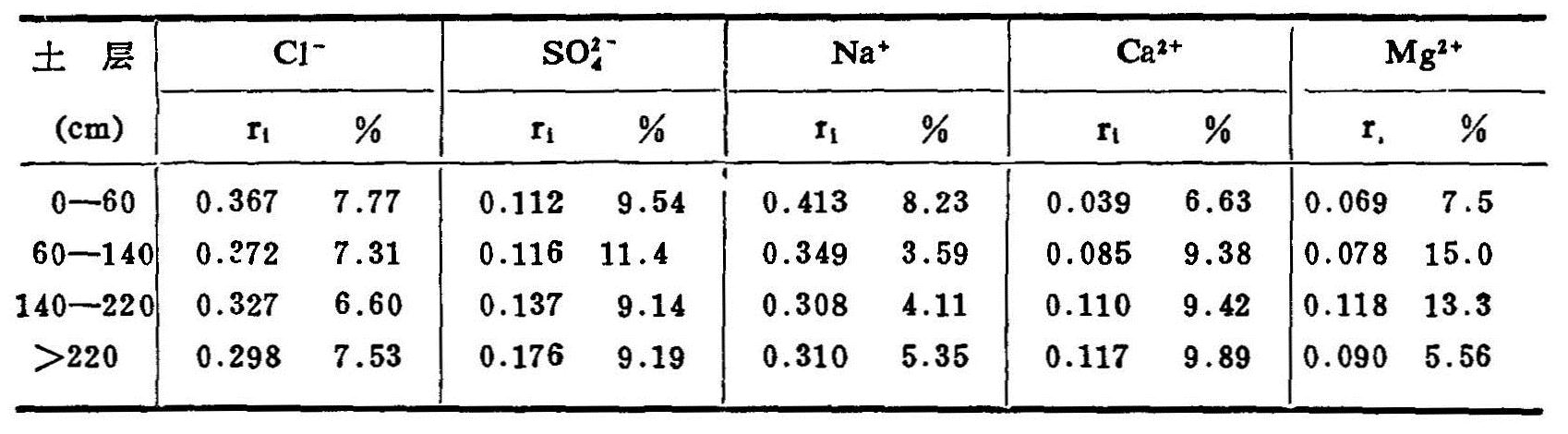
前面假定,剖面离子组成分数r 在某一季节和某一土层内,可能维持一个基本不变的常数。表6.8是1987年观测期间4—8月共5个月的离子组成变化统计表。从中可见整个土壤剖面分成4个土壤层段,每个层段内的离子组成分数,在此期间的变化幅度绝大多数都<10%,Mg2+的变化稍大一些。表中的%是通过每一层段在各次观测中得到的r
在某一季节和某一土层内,可能维持一个基本不变的常数。表6.8是1987年观测期间4—8月共5个月的离子组成变化统计表。从中可见整个土壤剖面分成4个土壤层段,每个层段内的离子组成分数,在此期间的变化幅度绝大多数都<10%,Mg2+的变化稍大一些。表中的%是通过每一层段在各次观测中得到的r 的均方差,除平均值后得到的,可说明r
的均方差,除平均值后得到的,可说明r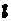 在每次观测中的变异情况。表中变化最小的是Na+,其次是Cl-、Ca2+和
在每次观测中的变异情况。表中变化最小的是Na+,其次是Cl-、Ca2+和![]() ,Mg2+变动较大。
,Mg2+变动较大。
表6.8 离子组成系数r1统计结果(1987.4—8.)
(三)模型的检验
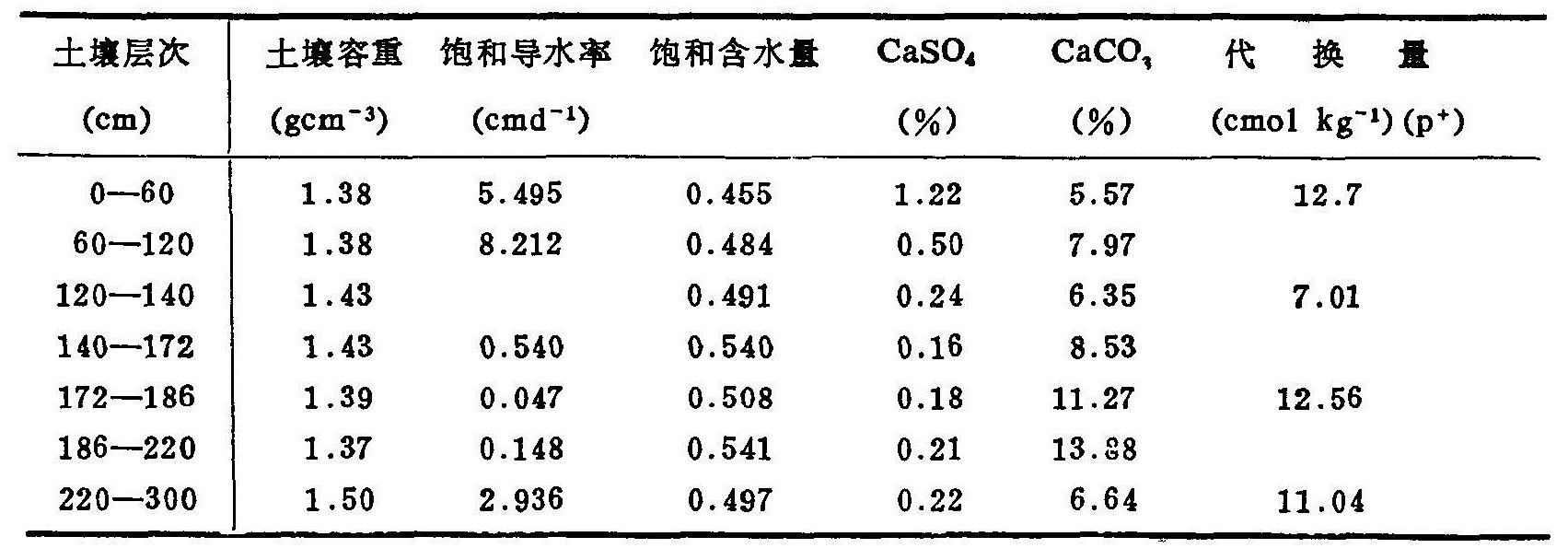
模型检验是通过田间试验的实测值与计算值的比较进行的。全部试验在河北省曲周县北京农业大学试验站完成。实测时段从1987年4月1日至同年8月31日,共5个月。表6.9列出了土壤剖面的几项物理与化学性质。土壤非饱和导水率和比水容量是用水分特征曲线数据,通过3次样条加密后用Jackson方法计算出来的。
土壤水盐实验是在一个观测井的装置内进行的。井的观测面分层埋设张力计、溶液抽提器和盐分传感器。中子管安排在井的观测方向上,分3个重复。观测周期为10天,全部观测项目在一天内完成。
表6.9 土壤剖面主要的物理与化学性质
第101天、121天和152天的盐分计算值和实测结果分别通过图6.19-a、b表示出来。图中散点是实测值,实线为计算值,单点线为不考虑源汇作用时计算出来的结果。
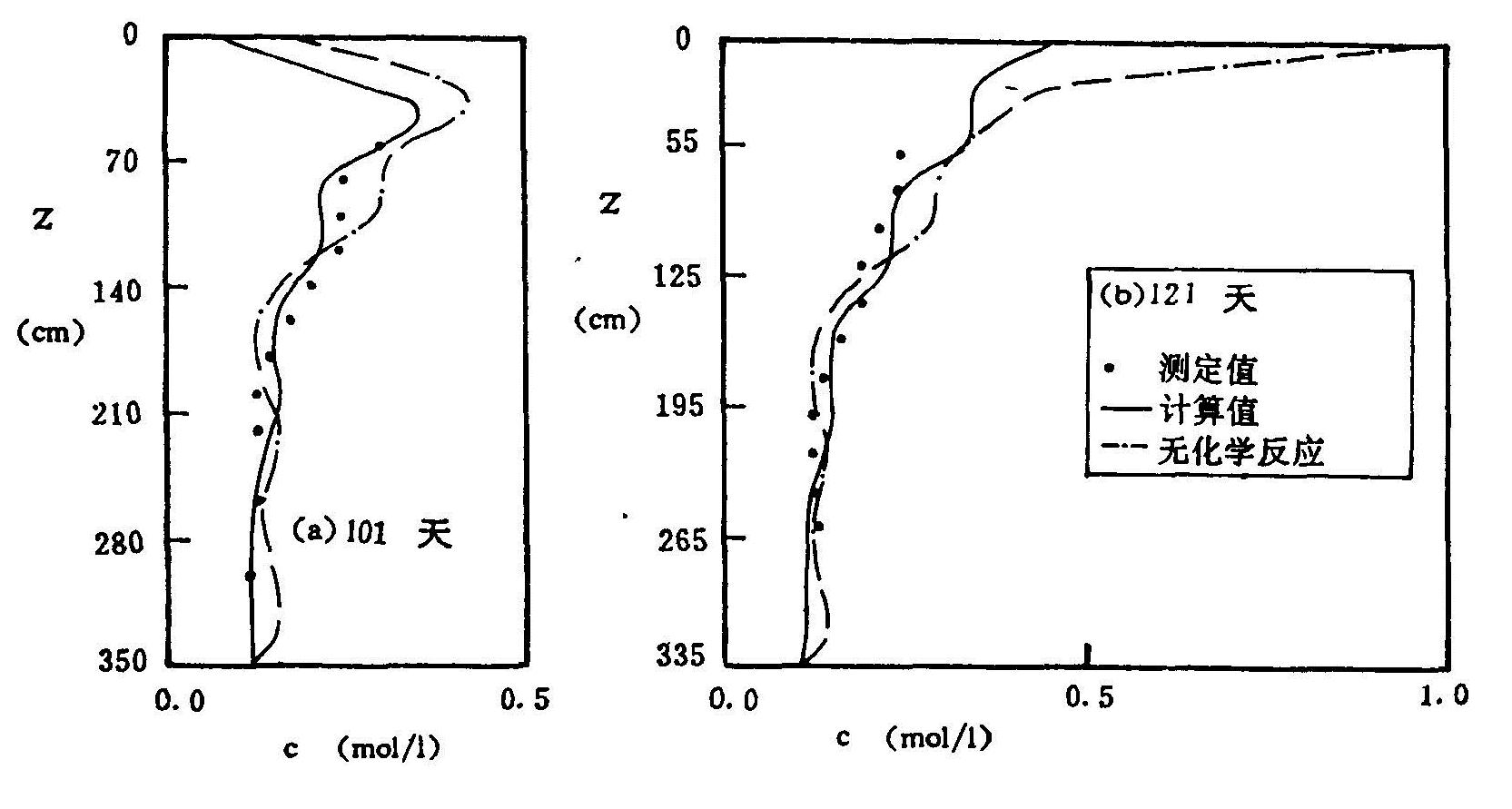
图6.19 有源汇作用与无源汇作用条件下土壤溶液浓度模拟值与实测值的对比(实线代表有源汇项,单点线表示无源汇项,散点为实测值)
由图看出,除实线与散点拟合最好外,无源汇作用的计算值与实测值符合也较好,它与前者的区别只在于土壤剖面上部的浓度要大,这可能是由于硫酸钙的化学沉淀作用影响所致。图6.19-a描述了经过一次雨后的淋洗剖面,由于前一天降雨达57.9毫米,土壤表层盐分迅速下移,图6.19-b则是一个雨后盐分的蒸发剖面,盐分强烈表聚。
Melamed等(1977)的实验结果表明,溶度积Ksp作为化学沉淀一溶解的阀值,能较大地决定模型计算结果的“命运”。图6.20-a、b也作了这样一个对比,即如果Ksp随土壤层次和时间作些变化(幅度很小)的话,则计算值与实测值的吻合程度有明显的改善。图中是仅举的几个例子,其中实线代表Ksp变化的情况,双点线代表不变的结果,散点为实测值。
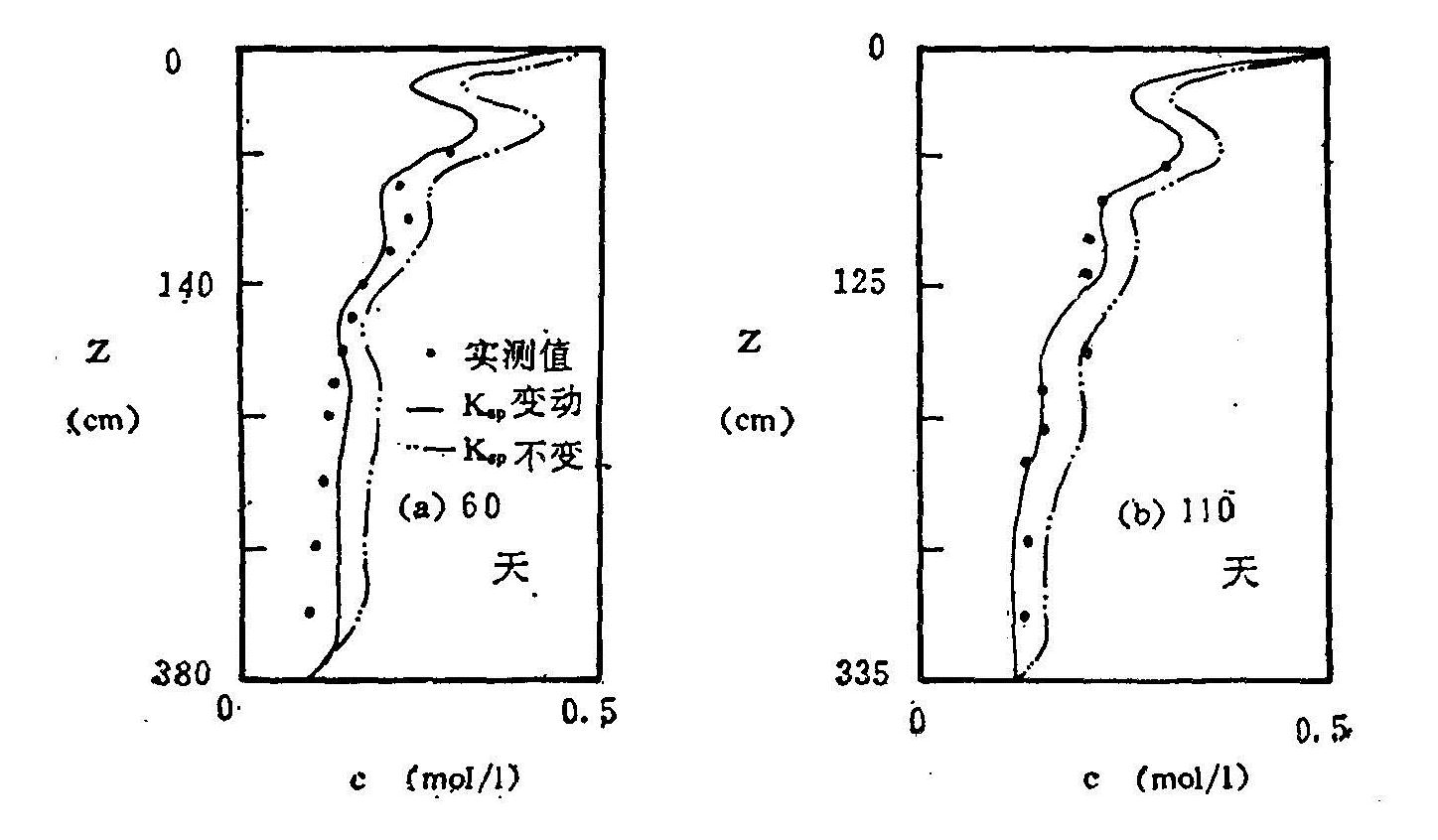
图6.20 Ksp变动与不变动情况下土壤溶液浓度的模拟值与实测值的对比
不难理解,Ksp的这些变化与土壤剖面中的![]() 和Ca2+,在不同土层和时间内遇到的物理和化学环境的不同有关,这就使得在某层能够沉淀的Ca2+和
和Ca2+,在不同土层和时间内遇到的物理和化学环境的不同有关,这就使得在某层能够沉淀的Ca2+和![]() ,而在另一条件下可能无法沉淀。这些物理和化学条件包含着极复杂的作用,影响到Ksp的波动。最明显的是温度对Ksp的影响。在计算过程中,7、8月份的取值(7.0×10-5)要比前几个月的(6.36×10-5)高一些则说明了这一点。土壤中碳酸钙的存在也影响到硫酸盐的沉淀,使其溶解度比原来小。由于实际土壤剖面的CaCO3含量是上部少于下部,所以下部的
,而在另一条件下可能无法沉淀。这些物理和化学条件包含着极复杂的作用,影响到Ksp的波动。最明显的是温度对Ksp的影响。在计算过程中,7、8月份的取值(7.0×10-5)要比前几个月的(6.36×10-5)高一些则说明了这一点。土壤中碳酸钙的存在也影响到硫酸盐的沉淀,使其溶解度比原来小。由于实际土壤剖面的CaCO3含量是上部少于下部,所以下部的![]() 要比上部容易沉淀,这与Ksp在计算中的变化相一致(>120厘米土层,Ksp取4.0 ×10-5;<120厘米的土层,Ksp取7.0×10-5)。总之,硫酸钙在土壤中的形成作用,是一个极其复杂的过程,对其精确的研究还需大量细致的工作。
要比上部容易沉淀,这与Ksp在计算中的变化相一致(>120厘米土层,Ksp取4.0 ×10-5;<120厘米的土层,Ksp取7.0×10-5)。总之,硫酸钙在土壤中的形成作用,是一个极其复杂的过程,对其精确的研究还需大量细致的工作。
AMDL模型描述了在田间非稳态水流条件下,5种离子(Ca2+、Mg2+、Na+、Cl-和![]() )在层状土壤中的综合运动,同时考虑了CaSO4的沉淀与溶解过程。模型中应用的盐分综合扩散弥散系数Dt,是各种离子D值的加权平均,其权重是相应离子占全盐量的分数ri。
)在层状土壤中的综合运动,同时考虑了CaSO4的沉淀与溶解过程。模型中应用的盐分综合扩散弥散系数Dt,是各种离子D值的加权平均,其权重是相应离子占全盐量的分数ri。
模拟结果表明,除非源汇反应项中的参数Ksp,随土壤剖面深度和时间作些轻微调整的话,模拟值与观测值符合不很理想。模型通过对化学反应的源汇作用取舍计算表明,有源汇项的计算值更接近实测值。
