二、模型的建立
以曲周水盐测报区为例，介绍所建立的土壤盐分多点动态预报模型。
预报时段：将一年分为4个时期，3月至6月，6月至9月，9月至12月，12月至翌年3月。3、6、9月都是关键的农事季节，预报这3个月份的土壤盐分状况，对于合理安排作物生产，进行有效地田间作物管理是有益的。
预报深度：可根据不同目的决定预报深度。本例作出了3种深度的预报，即0—40厘米（主要作物根系层），0—100厘米（影响作物生长的层次）和0—200厘米（可了解改良程度）。
变量选择：因变量为一定深度土体的盐贮量kgm-2，即Y40，Y100和Y200。
自变量有：
X1—SS（t-1）：前期盐贮量（kgm-2）；
X2—E0τ：用前一时段的水面蒸发，代替ET（mm）；
X3—d（t-1）：前期地下水水位（m）；
X4—Cg（t-1）：前期地下水水质，gl-1；
X5—（I+P）τ：前一时段的灌溉、降雨量之和，mm。
从盐渍化土壤发生演化角度出发，任何状态的盐渍化土壤其演化不是从高到低，就是从低到高，任何一种状态的盐渍化土壤，都可看作是盐渍化土壤发生演化过程中的一个阶段。这样可将测报区中空间上分布的任何一种状态的盐渍化土壤，看作是盐渍化土壤在时间上演化的一个阶段，而每一个状态所包括的几个点被看作重复。这样就扩大了统计量，使方程的代表性更大。本例所用资料始自1987年3月至1988年9月止，共57个点。
应用逐步回归统计方法，所建立的季度土壤盐分预报方程如表6.10。
表6.10 不同时间不同深度盐分预报方程
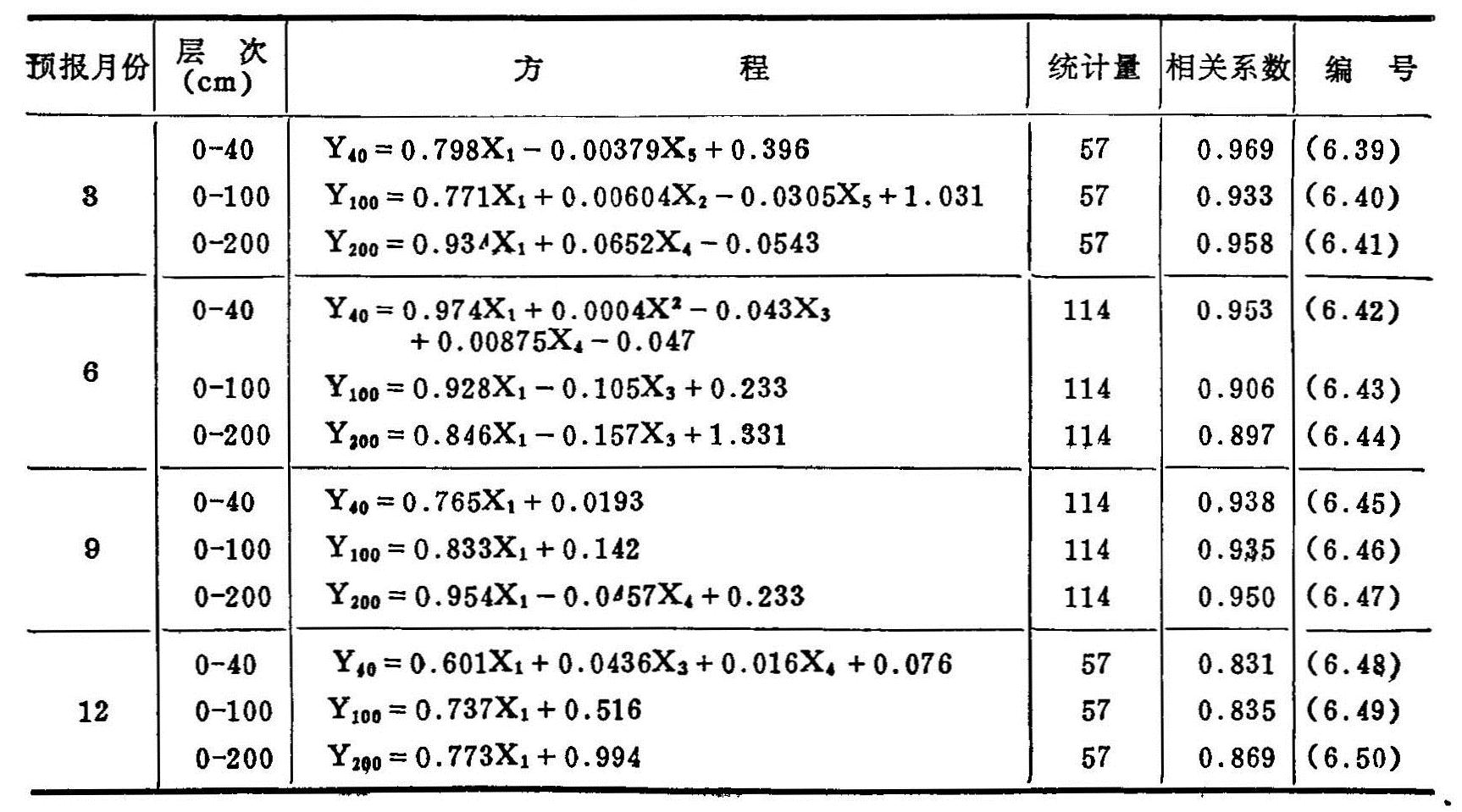
从所建立的方程中看出，初始含盐量都被选入，而且贡献最大。各方程的相关系数都很高，完全符合显著性水准。
各个方程相对误差＜20%的拟合情况见表6.11。
表6.11 各方程拟合情况表（拟合率%）
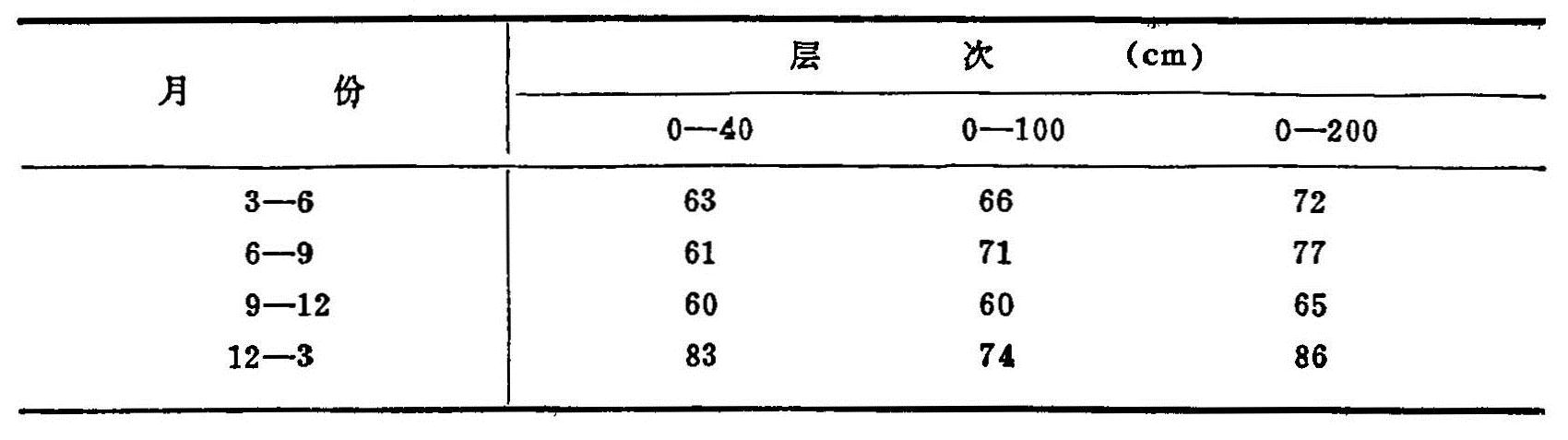
对同一地区，应用1987年资料，建立了包括粘土层厚度和层位，作为自变量的土壤盐渍化预报方程（李录久，1988）：
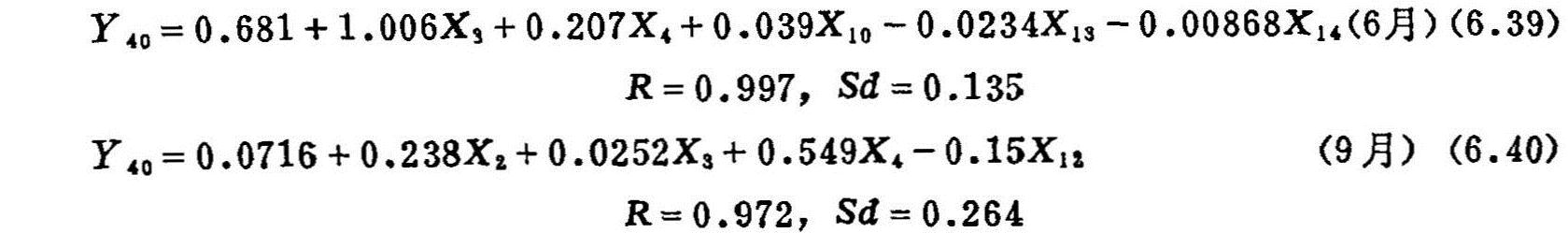
式中 X2、X3和X4：分别为0—100、0—40和0—20厘米初始盐贮量（kgm-2）；
X10：初始地下水矿化度（gl-1）；
X12：初始地下水埋深（m）的对数；
X13：前一时段的降雨总量，（mm）；
X14：前一时段的灌水总量（mm）。
粘土层因素未被选入。