预报模型的建立

一、预报模型的建立

（一）数学模型的建立

地下水水质的预报模型，也应选用确定型分布参数地下水水质数学模型。一般情形下，盐分的运动取决于对流运动与弥散过程，所以一般在区域地下水水质预报中选用对流一弥散型水质模型（Konikow，1981；孙讷正，1989）。对流—弥散水质模型的构成见图4.9（据孙讷正，1989）。其中①+②+③再加上⑤中的部分内容，即为4.2节中

建立的地下水水位动态预报的数学模型（见4.3式至4.10式）。一般情形下地下水运动的盐分对流一弥散方程与相应的定解条件可表达如下：

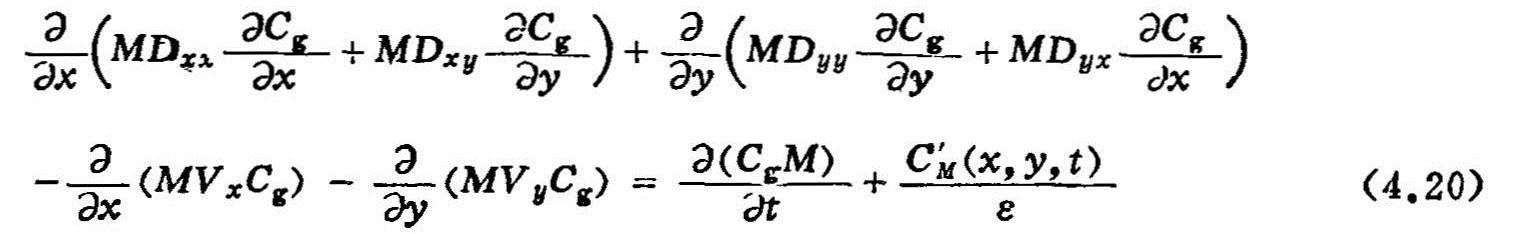
其中：

在忽略分子扩散情况下

式中　Cg：地下水矿化度（ML-3）；

ε：有效孔隙率；

：源或汇中的溶质量（M）；

Vx、Vy：在x、y方向实际流速（LT-1）；

Dxx，Dxy，Dyx，Dyy：水动力弥散系数各分量（L2T-1）；

aL：沿水流方向的弥散度（L）；

aT：垂直于水流方向的弥散度（L）；

V：水流的实际速度（LT=1）。

其余变量说明与式（4.3）相同。

（4.20）式定解条件为：

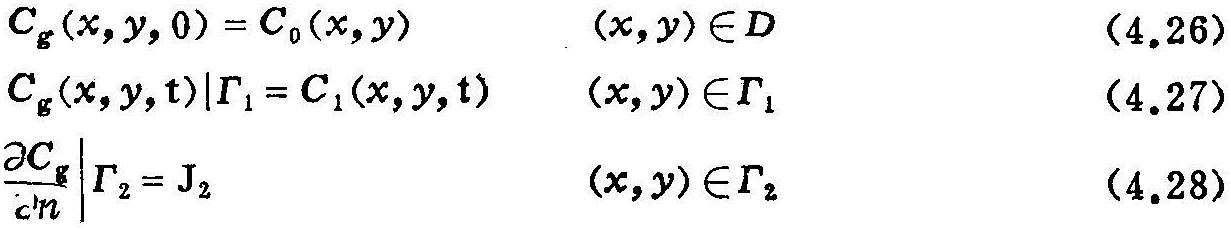
式中　Γ1、Γ2：一类、二类边界；

D：研究区域；

C0：初始浓度；

J2：浓度通量；

n：Γ2边界外法线方向；

C1：边界处浓度。

（二）数值方法

对式（4.20）求解，必须采用数值方法。同求解地下流方程相类似。一般情形下，有限元方法以其优越性而广泛地采用对地下水水质对流——弥散型方程求解。与求解（4.3）式地下水水位预报模型相一致，在PWS体系中，对区域地下水水质预报模型（4.20）式也宜采用有限元方法求解。

关于地下水水质对流—弥散方程的有限元方程推导过程，可参照有关文献（张蔚榛，1983；王秉忱，1985；孙讷正，1989），这里不再赘述。