2.4 Push⁃in Stability
There are two analysis methods for the push⁃in failure:free earth support method and fixed earth support method.As shown in Figure 2.13(a),the free earth support method assumes that the embedment of the retaining wall is allowed to move to a certain distance under the action of lateral earth pressure.Therefore,the earth pressure on the retaining wall in the limiting state can be assumed as shown in Figure 2.13(b).
The fixed earth support method is to assume that the embedment of the retaining wall seems to be fixed at a point below the excavation surface.The embedded part may rotate about the fixed point,as shown in Figure 2.14(a).Thus,when the retaining wall is in the limiting state,the lateral earth pressure around the fixed point on the two sides of the retaining wall does not necessarily reach the active or passive pressures,as shown in Figure 2.14(b).
If a cantilever wall is designed based on the free earth support method,no fixed point is supposed to exist in the embedded part of the wall,as discussed above.The external forces,only passive and active forces,on the retaining wall are not to come to equilibrium.Therefore,the free earth support method is not applicable to cantilever walls.On the other hand,if the free earth support method is applied to a strutted wall,the forces acting on the wall will include both the passive and active forces and the strut load.With external forces on the wall coming to equilibrium,the method is applicable to a strutted wall.On the other hand,if we apply the fixed earth support method to a strutted wall,the penetration depth of the wall will be too large to be economical.
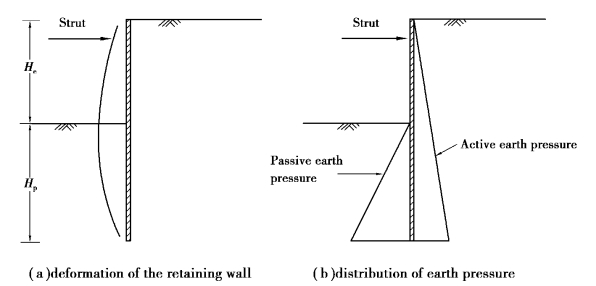
Figure 2.13 Free earth support method
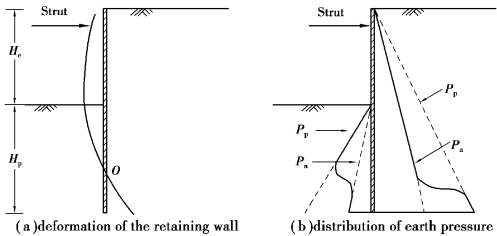
Figure 2.14 Fixed earth support method
For a strutted wall,the free earth support method is the commonly used analysis method.As shown in Figure 2.15(a),the earth pressures on the outer and the inner sides of the retaining wall in the braced excavation will reach the active and the passive earth pressures respectively in the limiting state.Take the retaining wall below the lowest level of strut as a free body and conduct a force equilibrium analysis[Figure 2.15(b)],and we can then find the factor of safety against push⁃in as follows:

where
Fp=factor of safety against push⁃in;
Mr=resisting moment;
Md=driving moment;
Pa=resultant of the active earth pressure on the outer side of the wall below the lowest level of strut;
La=length from the lowest level of strut to the point of action Pa;
Ms=allowable bending moment of the retaining wall;
Pp=resultant of the passive earth pressure on the inner side of the retaining wall below the excavation surface;
Lp=length from the lowest level of strut to the point of action Pp.
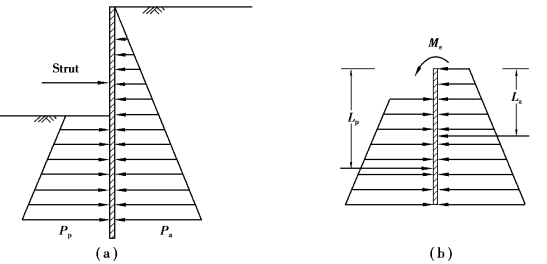
Figure 2.15 Analysis of push⁃in by gross pressure method
Equation 2.14 is generally called the gross pressure method.JSA(1988)and TGS(2001)suggested Fp≥1.5.Nevertheless,when assuming Ms=0,Fp≥1.2.Eq.2.14 can be used either to obtain the factor of safety against push⁃in for a certain depth of wall or the required penetration depth of a retaining wall with a certain value of safety factor.
As to short⁃term behavior of cohesive soils,their earth pressures should be obtained following the total stress method while parameter of soil strength should be derived from the UU test,the FV test,or the CPT test.If the cohesive soil is 100% saturated,it should be analyzed assumingφ=0.Rankine’s earth pressure can be employed:

where
σa=total active earth pressure(horizontal)acting on the retaining wall;
σp=total passive earth pressure(horizontal)acting on the retaining wall;
c=cohesion;
Ka=coefficient of active earth pressure;
Kp=coefficient of passive earth pressure.
When cohesive soils are completely saturated,φ=0 and c equals the undrained shear strength;that is,Ka=Kp=1.
For cohesionless soils,the excess pore water pressure dissipates quickly as soon as shearing occurs.As a result,the analysis should follow the effective stress method.Supposing there exists friction between the retaining wall and the surrounding soil,the earth pressure for design can be represented as follows:
![]()
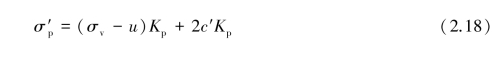
where
σ′a=effective active earth pressure acting on the retaining wall;
σ′p=effective passive earth pressure acting on the retaining wall;
c′=effective cohesion intercept;
u=porewater pressure.
For most cohesionless soils,the horizontal component of earth pressure are Ka,h=Ka cosδ,Kp,h=Kp cosδ.The friction angle between retaining walls and sandy soilsδis suggested to be 0.5~0.67 effective friction angle of soils(φ′).
For cohesionless soils,the pore water pressure u is not the hydrostatic but affected by seepage.Flow net can be used to estimate the variation of water pressure.Considering the difficulty of the depiction of a non⁃homogeneous and non⁃isotropic flow net,for the sake of simplification,we sometimes assume that the behavior of seepage is one dimensional,that is,the head loss per unit length of a flow path is the same.
As shown in Figure 2.16(a),the difference of the total heads between the upstream water level(outside the excavation zone)and the downstream water level is(He+di-dj).The length of the path of the water flowing from the upstream water level along the retaining wall down to the downstream water level is(2Hp+He+di-dj).Assuming that the datum of the elevation head is set to be the same with the upstream water level,the total head(h)at a distance of x from the upstream water level would be
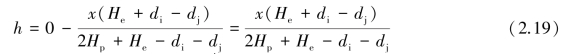
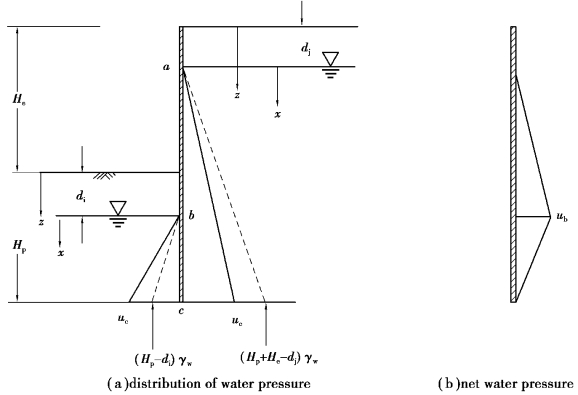
Figure 2.16 Simplified analysis method for seepage
Let he be the elevation head and hp pressure head.The pressure head at a distance of x from the upstream water level would be
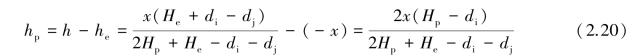
Thus,the water pressure,ux at a distance of x from upstream water level would be

The largest net water pressure is to be found at b,whose value would be
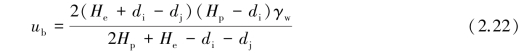
Seepage will decrease the porewater pressure on the active side(lower than the hydrostatic water pressure)and increase it on the passive side(higher than the hydrostatic water pressure).As discussed earlier,we can derive the rates of increase of porewater pressure per unit length on the active and passive sides as follows:

where ua and up represent the rate of increase of the porewater pressure per unit length on the active and passive sides,respectively.
Thus,the water pressure x below the water level at the active and passive sides are separately ux=μax(the active side)and ux=μpx(the passive side).
Therefore,μa andμp can be seen as the modified unit weights of water on the active side and passive side,respectively.As a result,the total lateral earth pressure at a depth of z below the ground surface on the back of the wall would be
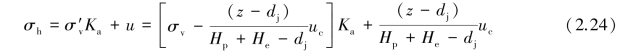
Similarly,the total lateral earth pressure at a distance of z below the ground surface on the front of the wall would be
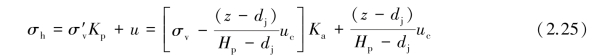
Alternatively,the active and passive earth pressures on the two sides of the retaining wall are expressed in terms of net values.By conducting a force equilibrium of the net forces on the retaining wall below the lowest level of strut,Equation 2.12 is also available to compute the factor of safety against push⁃in.This method is called net pressure method.Nevertheless,according to Burland and Potts(1981),and Ou and Hu(1998),any slight difference of the penetration depth will lead to a large change in the factor of safety computed from the net pressure method.That is to say,the factor of safety is too sensitive to the penetration depth and this method is not good for stability analysis of the push⁃in failure.
Example 2.1
An excavation in clay goes 9.0 m into the ground(He=9.0 m).The groundwater outside the excavation zone is at the ground surface level while that within the excavation zone is at the level of the excavation surface;γsat=17.0 kN/m3.The undrained shear strength su=45 kN/m2.Suppose the excavation width B=10 m and the excavation length L=30 m.Compute the factor of safety against basal heave according to Terzaghi’s method and Bjerrum and Eide’s method,respectively.
Solution:
According to Terzaghi’s method,
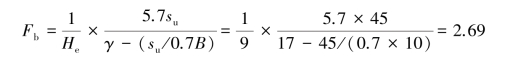
According to Bjerrum and Eide’s method,According to Fig 2.6,Nc=7.1,
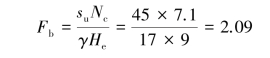
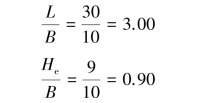
Example 2.2
The same as Example 2.1 except that there exists a stiff clayey layer 4.0 m below the excavation surface and the undrained shear strength of the clay is 80 kN/m2.Compute the factor of safety against basal heave according to Terzaghi’s method and Bjerrum and Eide’s method,respectively.
Solution:
According to Terzaghi’s method,
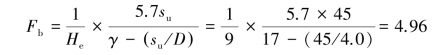
According to Bjerrum and Eide’s method,
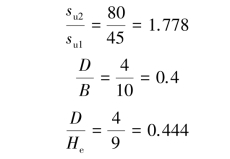
According to Fig 2.7(a)and(b),Nc,s=6,
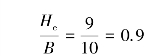
According to Fig 2.7(c),fd=1.22
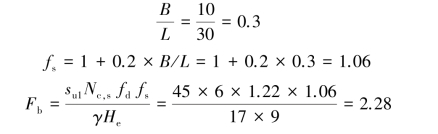
Example 2.3
An excavation in completely saturated clay goes 9.0 m into the ground(He=9.0 m)and the lowest level of struts is 2 m above the excavation surface.The groundwater outside the excavation zone is at the ground surface level while that within the excavation zone is at the level of the excavation surface.γsat=17.0 kN/m3.The undrained shear strength su=45 kN/m2.Assume the penetration depth Hp=2 m and ignore the allowable bending moment of the retaining wall Ms,compute the factor of safety against push⁃in.
Solution:
When cohesive soils are completely saturated,Ka=Kp=1
Active earth pressure:
At the lowest level of strut
σa1=σvKa-2cKa=17×7-2×45=29 kN/m2
At the toe of the retaining wall
σa2=σa1+4×17=97 kN/m2
Resultant of the active earth pressure below the lowest level of strut
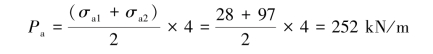
Length from the lowest level of strut to the point of action Pa
![]()
Passive earth pressure:
At the excavation bottom
σp1=σvKp+2cKp=17×9+2×45=243 kN/m2
At the toe of the retaining wall
σp2=σp1+2×17=277 kN/m2
Resultant of the passive earth pressure below the lowest level of strut
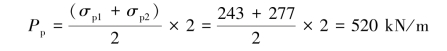
Length from the lowest level of strut to the point of action Pp
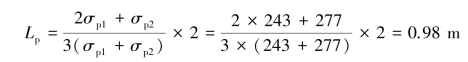
The factor of safety against push⁃in
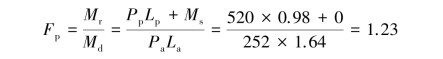
Example 2.4
A 9.0 m deep excavation in a sandy ground and the lowest level of struts is 2.5 m above the excavation surface.The level of groundwater outside the excavation zone is at the ground surface level while that within the excavation zone is as high as the excavation surface.The unit weight of saturated sandy soilsγsat=20 kN/m2,the effective cohesion c′=0,and the effective angle of frictionφ′=30°.Assume that the friction angles(δ)between the retaining wall and soil on both the active and passive sides are 0.5φ′and the factor of safety against push⁃in,Fp=1.5.Compute the required penetration depth(He).
Solution:
Let z represent the depth from the ground surface and x depth from the groundwater level
①Determine the coefficient of the earth pressure:
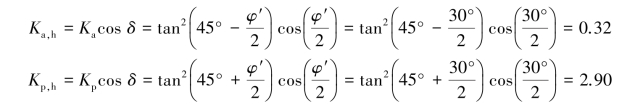
②Compute the effective active earth pressure on the wall:
According to Eq.2.19,the porewater pressure at x away from upstream water level would be
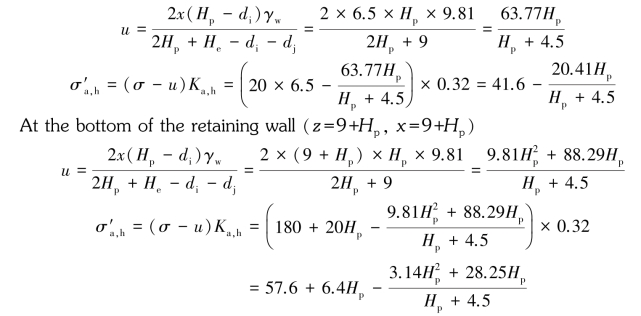
③Compute the lateral effective passive earth pressure on the wall:
At the bottom of the wall
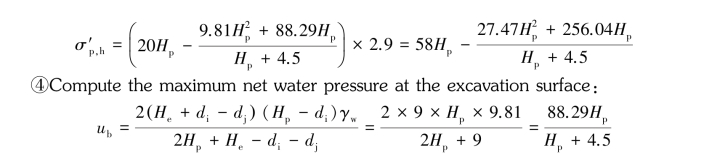
⑤Compute the driving moment and resistant moment for the free body below the lowest level of struts:
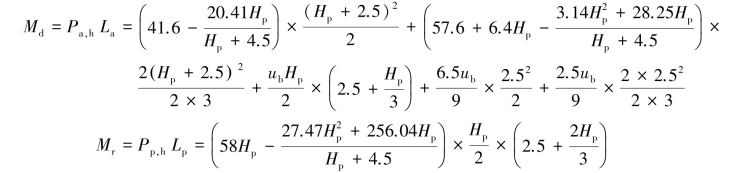
⑥Determine the penetration depth(Hp):
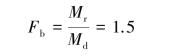
Then we have Hp=17.4 m.
