8.3.1 Full penetration wells
Permeable layers are also designated as aquifers.When both above and below an aquifer,with the piezometric level higher than the top of the aquifer and impermeable layers being found,the aquifer is called a confined aquifer.
When pumping an aquifer with a single well,the piezometric level will decline and a virtual drawdown cone will be formed,centered at the well,as shown in Figure 8.8.From the beginning of pumping,the area of the virtual drawdown cone will grow with the continuation of pumping.After a long period,the expansion rate of the area of the virtual drawdown cone will decline or stop expanding.This section is to introduce the pumping⁃induced drawdown according to the penetration depth of the well into an aquifer and the expansion conditions of the virtual draw down cone.
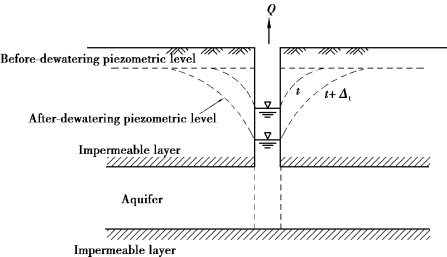
Figure 8.8 Dewatering in confined aquifers
1)Full penetration wells
A full penetration well is one that fully penetrates through the aquifer and its flow direction is thus horizontal[Fig 8.9(a)].An equation of the drawdown curve with regard to time by Theis(1935)can be derived based on the following assumptions:
①The aquifer has a uniform thickness and is a homogeneous and isotropic confined aquifer.
②The well has to be one that fully penetrates through the aquifer.
③The well is 100% efficient.That is to say,no drop exists between the water table in the well and the drawdown curve.
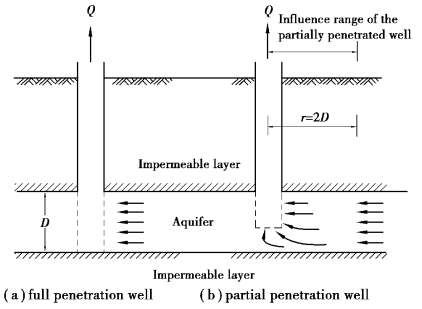
Figure 8.9 Flow directions around a well in confined aquifers
④Meets the Dupuit⁃Thiem assumption.That is,the hydraulic gradient of any point on the drawdown curve is the slope at the point.
⑤No recharge water is within the influence range.
⑥The radius of the well is so small that the amount of retained water can be ignored.
Then the equation is written as follows(Figure 8.10):
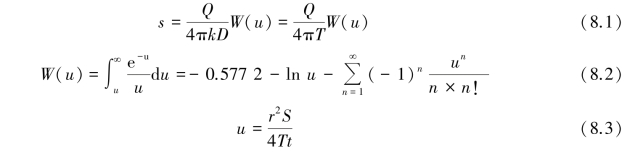
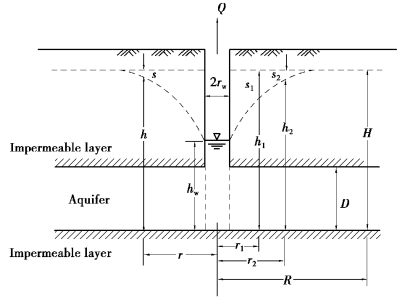
Figure 8.10 Symbol of dewatering in confined aquifers
where
s=drawdown;
Q=discharge quantity;
k=coefficient of permeability;
D=thickness of the aquifer;
T=kD=coefficient of transmissivity;
W(u)=well function;
u=parameter of the well function;
r=distance to the center of the well;
S=coefficient of storage or storativity.The coefficient of storage,which generally ranges between 0.000 5⁃0.001,is defined as the drained volume of the pore water due to lowering a unit head per unit surface area of an aquifer;
t=time since pumping started.
Eq.8.1 is Theis's(1935)nonequilibrium equation.Table 8.2 lists the values of well function calculated from Eq.8.2.Figure 8.11 is the W(u)-(1/u)relation curve calculated from Eq.8.2,which is also called the standard curve.
Table 8.2 Well function W(u)(Ferris et al.,1962)
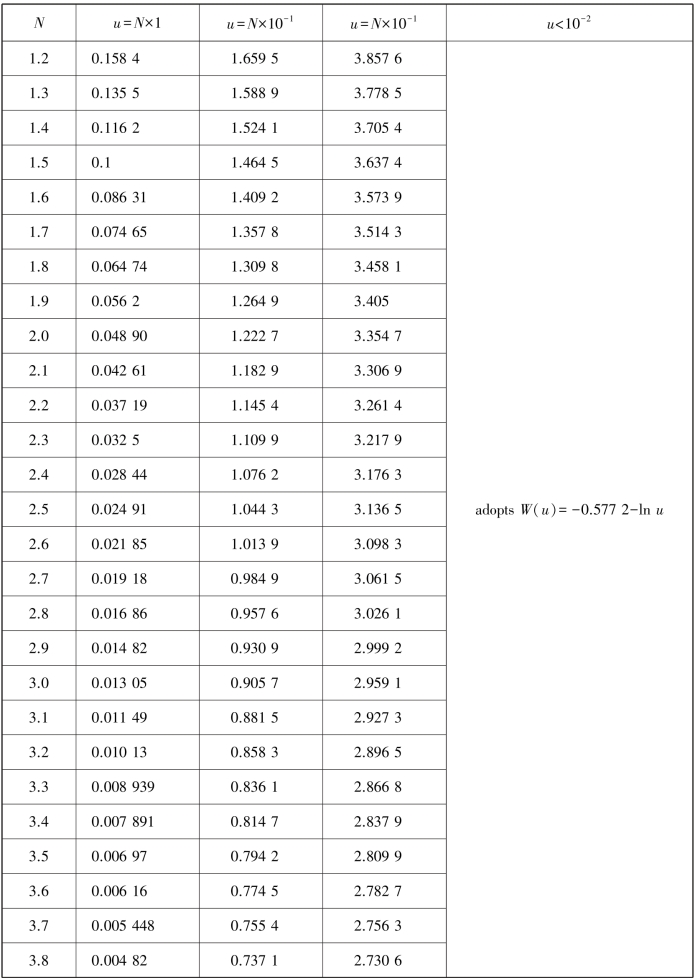
continued
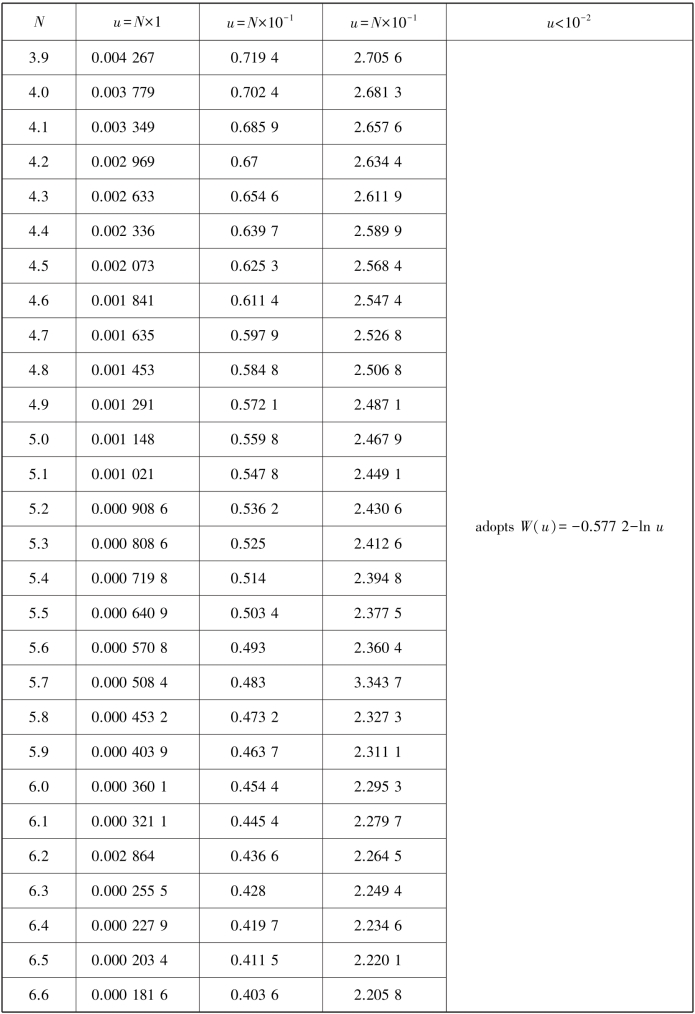
continued
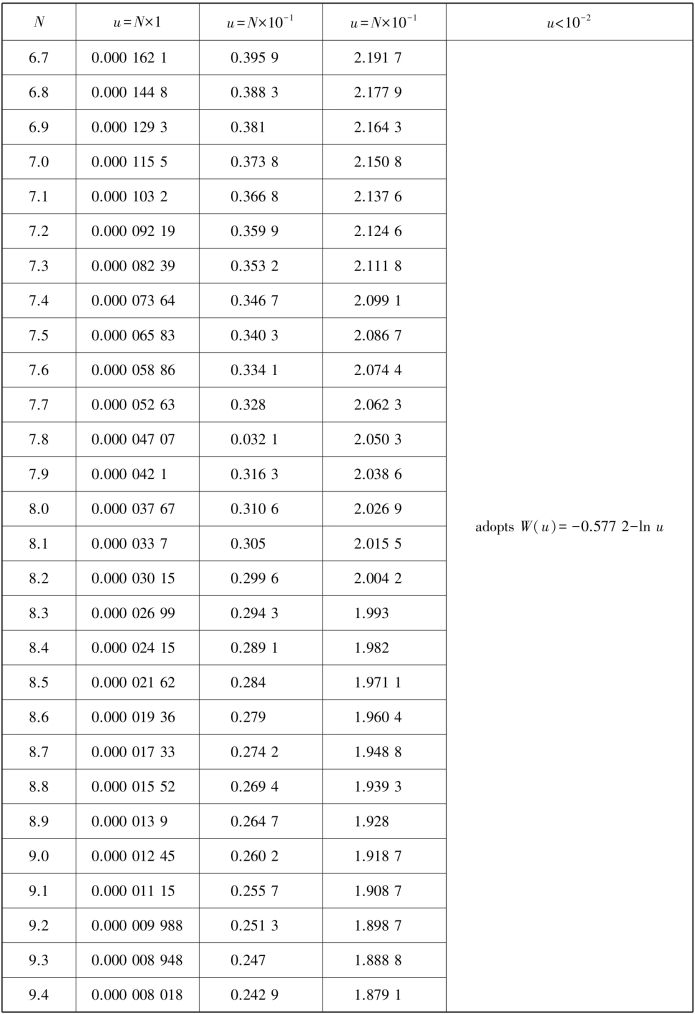
continued
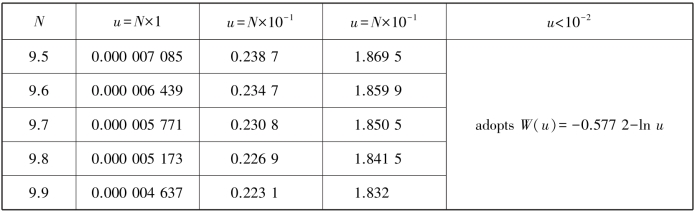
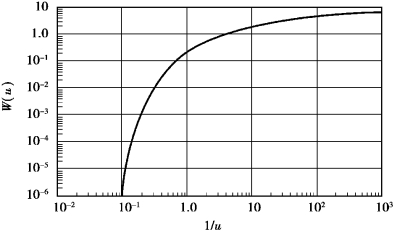
Figure 8.11 Standard curve of the well function(Ferris et al.,1962)
Habitually,the coefficients of permeability,transmissivity,and storage are all called hydraulic parameters.The coefficient of permeability is an intrinsic parameter of a soil,the coefficient of transmissivity is the coefficient of permeability multiplied by the thickness of the aquifer.Since the thickness of a confined aquifer is a constant,the coefficient of transmissivity of a confined aquifer is also a constant.
The coefficient of storage is defined as the drained volume of the pore water due to lowering a unit head per unit surface area of an aquifer.Since soil in a confined aquifer is always in the saturated state,the drainage of pore water during dewatering should be caused by the decrease of the thickness of the aquifer.Since the decrease of heads follows the increase of effective stress,the thickness of the aquifer will reduce as a result.Following the above elucidation,the coefficient of storage of a confined aquifer,which generally ranges between 0.000 5⁃0.001,is similar to the compressibility of soils.
When pumping time(t)is rather long or the distance(r)is quite short,the parameter u will be very small.Thus,when u≤0.05,the high order of the multinomial at the right side of the equation can be ignored.Equation 9.2 can then be rewritten as
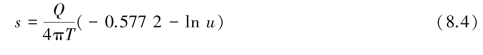
which can also be written as

Eq.8.4 or 8.5 is called Jacob's modified nonequilibrium equation(Jacob,1940),which is only applied when u≤0.05.
Assuming the influence range of pumping is defined as the distance where the draw down just declines to 0,the influence range of pumping⁃induced drawdown(R)can be calculated from Eq.8.5 as

In addition,another empirical formula could be used to estimate the influence range Sichart(1928)
![]()
where
sw is the drawdown in the well.
Assume the drawdown curve achieves equilibrium after pumping,(which follows that the drawdown curve will not expand with regard to pumping time).Thiem's equilibrium(Thiem,1906)can thus be derived from the differential equation of the drawdown curve:

where
r1 and r2 are the distances of the first observation well and the second observation well to the well center,respectively;
s1 and s2 are drawdowns in the first and the second observation well,respectively.
Let R be the influence range and R/r substitute for r2/r1,Eq.8.8 can be derived to compute drawdown at any distance:

Let the drawdown in the well be(H⁃hw),the radius of the well be rw,we can have

Eq.8.11 is derived from the differential equation of the drawdown curve,assuming that drawdown after pumping is in equilibrium and that the drawdown curve does not expand with pumping time.Substitute the influence range(R)of Eq.8.6 into Eq.8.5,Jacob's modified nonequilibrium equation,we then have Eq.8.8.Thus,Thiem's equilibrium equation is a special case of Jacob's modified nonequilibrium equation.That is to say,when the drawdown curve does not expand any more,the pumping time coming to t and the influence range extending to R,Jacob's modified nonequilibrium equation will be identical to Thiem's equilibrium equation.
After pumping for a period of time,tum off the pump and the drawdown curve will gradually return to the original water table.The relationship between the recovered draw down curve and time can obtain the coefficient of transmissivity or permeability,as is designated as the recovery method.According to Theis(1935),the relationship between the residual drawdown and time can be expressed as follows:
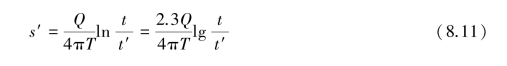
where
s′=residual drawdown,that is,the distance between the water level in the pumping well and the original groundwater level;
Q=recovered quantity,equivalent to discharge quantity;
T=coefficient of transmissivity;
t=time since pump started;
t′=time since pump is stopped.
The recovery method can be used to examine the results of pumping tests.What's more,during a long period of pumping and dewatering,the activities of pumping may be suspended temporarily for certain reasons and the drawdown curve will recover gradually.The recovery method can be used under such conditions.The results can not only offer extra data but be compared with those of pumping tests.
2)Partial penetration well
In practice,the partial penetration well is more widely used than the full penetration well[Figure 8.9(b)].Within the range of r≤2D,the flow lines in the vicinity of the well are not necessarily horizontal.Instead,some are vertical.For most types of soils,the vertical coefficients of permeability are about one⁃tenth of the horizontal one.Thus,the well formulas concerning partial penetration wells need modifying.
Considering the nonequilibrium theories for partial penetration wells are quite complicated,we leave them aside and only introduce an equilibrium theory by Kozeny(1953).
As shown in Figure 8.12,when r>2D,the effects of a partial penetration well can be ignored since its drawdown curve can be fully solved when seen as a full penetration well.When r≤2D,however,the amount of drawdown for a partial penetration well is larger than that for a full penetration well,and the quantity of water to be pumped to achieve the designed drawdown can be expressed as follows:
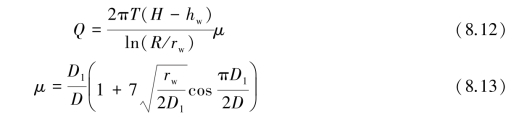
Where
μ=coefficient of modification;
D1=penetration depth of the well;
D=thickness of the aquifer.
Other parameters mean the same as in the equation of the full penetration well.
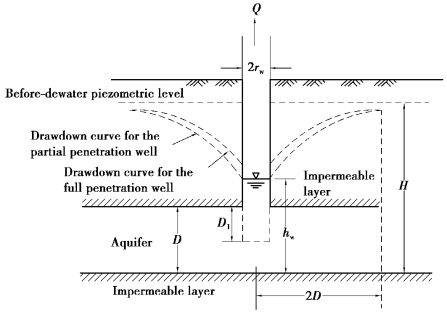
Figure 8.12 Drawdown curve for partial penetration wells in confined aquifers
