12.4.1 Maximum likelihood method
Ledesma et al.（1996）illustrated a maximum likelihood to perform back analysis.The formulation allows the introduction of the error structure of the observations and gives a minimum bound of the variances of the parameters identified.The formulation results in a minimization problem of an“objective function”，which can be solved by means of any suitable optimization technique.
1）Basic formulation
It is assumed that a relation between state variables，x and parameters，p，has been defined by means of a model，M（generally non⁃linear）which is considered fixed：x＝M（p）.The information available includes some measurements，that is，a set of measure set variable，x∗，and some prior information on the parameters to be estimated，p∗.
In the maximum likelihood approach，the best estimation of the system parameters is found by maximizing the likelihood of a hypothesis，L.Likelihood is defined as proportional to the joint probability of errors in measuring state variables and in the prior information of the parameters：
where measured state variables and parameters have been considered as independent.
Assume that the model is correct and differences between measured values，x∗，and the values computed using the model，x，are due to the error measurement process.Also，differences between the prior information on the parameters，p∗，and the parameters to be estimated，p are due to the error in that prior information.Therefore，when Eq.12.29 is used，we are maximizing the probability of reproducing the errors we have obtained in the measurement process and in the generation of prior information.
If probability distributions are supposed to be multivariate Gaussian，then
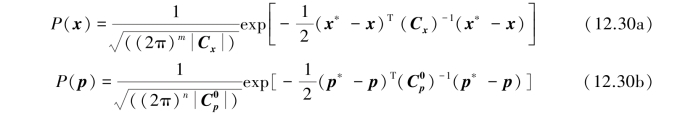
where（x∗－x）is the vector of differences between an computed values measured by using a fixed model，（p∗－p）is the vector of differences between prior information and parameters to be estimated，Cx is the measurements covariance matrix，which represents the structure of the error measurements，C0p is the a prior parameters covariance matrix，which represents the error structure of the available prior information，m is the number of measurements，n is number of parameters，（ ）T is used to indicate a transposed matrix，and｜｜is the determinant symbol.
Note that in（ ），L＝L（p），i.e.likelihood depends only on parameters，because the relationship x＝M（p）is introduced in the probability density function（Eq.12.30a）.Maximizing L is equivalent to minimize the function S＝－2 ln L（p），that is
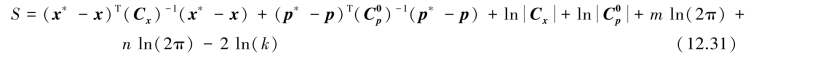
where the last three terms are constant and can be disregarded in the minimization process.
Eq.12.31 shows that the function to be minimized，i.e.objective function，depends on the error structure of measurements and prior information through the covariance matrices which are usually difficult to define.Generally，the information available will not be sufficient to specify all the elements of the covariance matrices and some terms will have to be fixed.To do that，it is convenient to separate measurements and prior information in groups with independent covariance matrices.For instance，if m measurements have been obtained from r independent instruments and n parameters can be divided in s groups with individual a priori covariance matrices，then the objective function，S，becomes
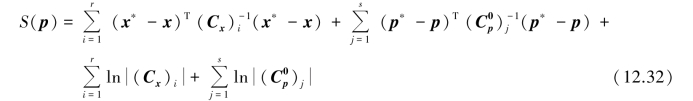
It should be pointed out that when no prior information is available，only the first and third terms in Eq.12.32 must be considered.Moreover，if measurements are independent and all of them have the same variance，we obtain Cx＝σ2I where I is the identity matrix.If the value ofσ2 is fixed in the process，only the first term in Eq.12.32 is relevant and classical least⁃squares criterion is obtained from that equation.
2）Variance estimation
It is convenient to express each individual covariance matrix as
whereσ2 plays the role of a scale factor which represents the global variance of the data，whereas the Ex and E0p matrices represent the error structure associated with that particular type of data.
Generally，the error structure is constant，that is，it depends only on the measurement instrument or on the procedure used to obtain the prior information on the parameters.
The global variancesσ2 could be determined from the standard error of the measurement device，but in general there are uncontrolled factors that influence that value，for instance，operator skill or equipment conditions.Therefore，those values are difficult to determine in practice，not only for the measurement covariance matrices but usually also for the prior information covariance matrices.Hence，it is convenient to consider those global variances as additional parameters to be identified.This is consistent with the maximum likelihood approach.Introducing Eqs.12.33a and b into the objective function Eq.12.32 leads to
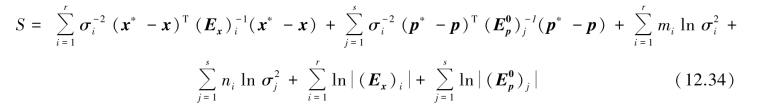
where mi and ni are the dimensions of the individual covariance matrices.The last two terms are now constant（assuming fixed the error structure and only variable the global errorσ2）and will not be taken into account in the minimization process.
Any procedure to minimize function Eq.12.34 can be adopted.Note that the objective function now depends both on the parameters and on the variances.However，the minimization problem can be simplified uncoupling the estimation of parameters from the estimation of variances.This is convenient from a practical point of view，as conventional formulations are geared to the identification of parameters only.The minimization is then performed in an iterative two⁃step procedure：particular values of the variances are first selected and the minimization process is carried out to identify only parameters.Variance values are varied according to an independent optimization procedure until the global minimum is obtained.
To show the validity of this approach，let us consider first a set ofμi＝σ∗2／σ2i fixed，where σ∗2 is any variance taken as reference.This is equivalent to performing a constrained minimization of Eq.12.34.The extended Lagrangian of function Eq.12.34 is
i.e.
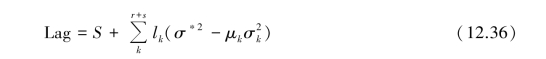
where lk is a Lagrange multiplier.After deriving Eq 12.36 with respect to the variances，imposing the minimum condition and eliminating li，from the equations，the following equations are obtained：
where
Substituting Eqs.12.37a and b in Eq.12.34 leads to a condition for S in the minimum：
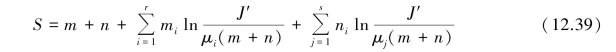
Note that in Eq.12.39 the dependence of parameters is through J′.Moreover，as Eq.12.39 is a monotonic function of J′，a minimum of J′will minimize S as well.
The general problem was defined as finding a set of parameters，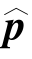
and variances
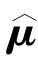that minimized Eq.12.34.Therefore，if
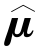is found using an independent algorithm，the parameters 
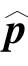that minimize S（p，μ）will also minimize for those
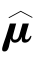values.This result allows to uncouple the minimization procedure：i.e.by minimizing J′，different sets of
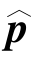for different values of
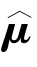are found.The values
that minimize S are obtained via a direct search algorithm.
3）Parameters reliability
The maximum likelihood formulation provides a statistical framework within which information on the reliability of the parameters estimated can be obtained.For instance，the covariance matrix of the estimated parameters（a posteriori covariance matrix）is（Tarantola，1987）
where A is the sensitivity matrix（m×n）：
Eq.12.40 takes into account both the prior information and the measurement error to estimate the final covariance of the estimated parameters.It should be pointed out that Cp，computed from Eq.12.40 is a minimum bound of the parameters variance，due to the linearization of the model implicit in Eq.12.41.
4）Optimization procedure
The mathematical problem to be solved in order to perform the estimation of parameters is an unconstrained minimization of Eq.12.34.Following the procedure described above，the simpler Eq.12.38 can be used instead.Using different values of variances，associated values of J′are obtained by minimization of Eq.12.38.The global minimum of J′will give the parameters and variances finally estimated.
There are a wide range of algorithms available to find the minimum，but Gauss⁃Newton method is convenient for this kind of objective functions.In case of convergence difficulties，the extension of that method due to Levenberg⁃Marquardt algorithm（Marquardt，1963）usually gives good results.As the function to minimize is in general non⁃linear with respect to the parameters，the procedure works iteratively in the parameters’space.Hence，starting from a point in that space，the parameters correction is found by means of
whereΔp＝p∗－p，Δx＝x∗－x andλis a scalar which controls the convergence process.Ifλ→0，the Gauss⁃Newton method is obtained.Asλincreases，Ap tends towards the maximum gradient direction.Near the minimumλof 0（or a very small value）.No general rule exists to decide the value ofλto be used in each iteration.Usually，if J′becomes smaller in an iteration，λis decreased，reaching zero close to the minimum.However，if J′increases after using Eq.12.42，the value ofλis also increased in order to approach the gradient direction.In the examples presented in this book，the following criteria has been used：λ＝10 as initial value，and，λn＋1＝10λn if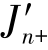
1＞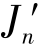
；otherwiseλn＋1＝λn／10，where n is the iteration number.