7.4.2 Applying the Hardin⁃Drnevich relationship in...
The decay of soil stiffness from small strains to larger strains can be associated with loss of intermolecular and surface forces within the soil skeleton.Once the direction of loading is reversed，the stiffness regains a maximum recoverable value which is in the order of the initial soil stiffness.Then，while loading in the reversed direction is continued，the stiffness decreases again.A strain history dependent，multi⁃axial extension of the Hardin⁃Drnevich relationship is therefore needed in order to apply it in the Hardening Soil model.Such an extension has been proposed by Benz（2006）in the form of the small⁃strain overlay model.Benz derived a scalar valued shear strainγhist by the following projection：
whereΔe is the actual deviatoric strain increment and His a symmetric tensor that represents the deviatoric strain history of the material.Whenever a strain reversal is detected，the tensor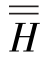 
is partially or fully reset before the actual strain incrementΔe is added.As the criterion for strain reversals serves a criterion similar to that in Simpsons brick model（1992）：All three principal deviatoric strain directions are checked for strain reversals separately which resemble three independent brick models.When there is no principal strain rotation，the criterion reduces to two independent brick⁃models.For further details on the strain tensor 
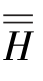and its transformation at changes in the load path，please refer to Benz（2006）.
The scalar valued shear strainγ＝γhist calculated in Eq.7.4 is applied subsequently used in Eq.8.33，the scalar valued shear strain is defined as
whereεq is the second deviatoric strain invariant.In triaxial conditions，γcan therefore be expressed as
Within the HS small model，the stress⁃strain relationship can be simply formulated from the secant shear modulus as
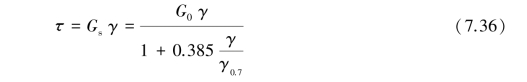
Taking the derivative with respect to the shear strain gives the tangent shear modulus：
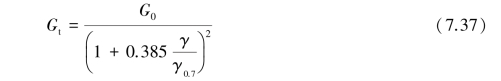
This stiffness reduction curve reaches far into the plastic material domain.In the Hardening Soil model and HS small model，stiffness degradation due to plastic straining is simulated with strain hardening.In the HS small model，the small⁃strain stiffness reduction curve is therefore bound by a certain lower limit，determined by conventional laboratory tests：
•The lower cut⁃off of the tangent shear modulus Gt is introduced at the unloading reloading stiffness Gur which is defined by the material parameters Eur and vur：
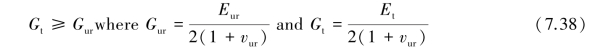
•The cut⁃off shear strain cut⁃off can be calculated as
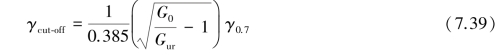
Within the HS small model，the quasi⁃elastic tangent shear modulus is calculated by integrating the secant stiffness modulus reduction curve over the actual shear strain increment.An example of a stiffness reduction curve used in the HS small model is shown in Figure 7.11.
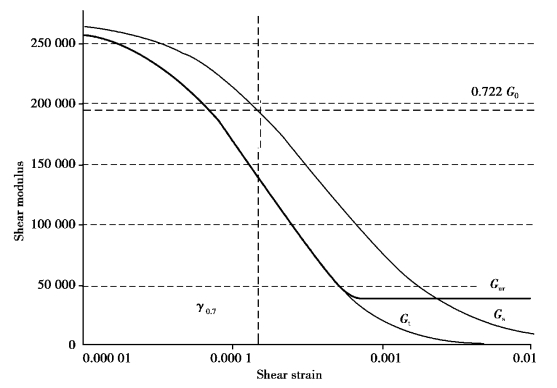
Figure 7.11 Secant and tangent shear modulus reduction curve
Moreover，the tangent shear modulus Gt and corresponding Young's modulus Et（considering a constant Poisson's ratio vur）is stress⁃dependent，and follows the same power law.For primary loading situations，the model uses the same hardening plasticity formulations as the Hardening Soil model，where Eur is replaced by Et as described above.