12.2.1 Formulation of an error function
To conduct an inverse analysis，we can use a function to evaluate the error between the experimental and numerical results.It must be between the experimental result and the numerical prediction，and measured by a norm value，which is referred to as an individual norm that forms an error function Ferr（x）：
where x is a vector containing the parameters to be optimized.Bound constraints are introduced on these variables，where xmin and xmax are，respectively，the lower and upper bounds of x.
As the first step in the formulation of an error function，an expression for the individual norm has to be established.In general，the individual norm is based on Euclidean measures between discrete points，composed of the experimental and the numerical results.The simplest error function can take the following expression：
where N is the number of values，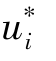
is the computed value，and ui is the value of observation.
Another formulation of the error function was introduced：
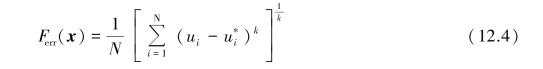
where k is a non⁃null positive value with k＝1 for the sum of error at every point and k＝2 for the least square function.
However，Eqs.12.3 and 12.4 present some disadvantages that the error is dependent on the type of test and the number of measurement points.To eliminate the scale effects on the fitness between the experimental and the simulated results，some normalized formula was developed.
Levasseur et al.（2008）adopted an advanced error function which can be adopted with 2 modifications of 100 percentage and add weight to each calculation point.The average difference between the measured and the simulated results is expressed in the form of the least square method：
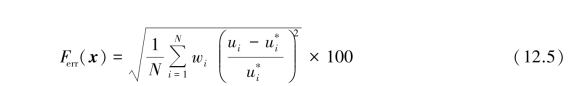
where wi is weight for the calculation at point i.