7.5.2 Yielding founction
The yield function of the Soft Soil model is defined as
where fis a function of the stress state（p′，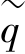
）and pp，the pre⁃consolidation stress is a function of plastic strain such that
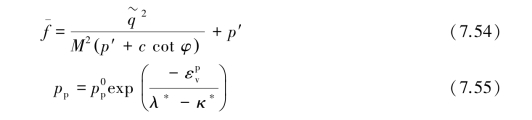
and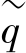 
is a similar deviatoric stress quantity as defined for the cap yield surface in the Hardening Soil model：
＝
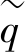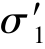＋（α－1）
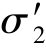－α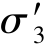
whereα＝（3＋sinφ）／（3－sinφ）.
The yield function（f＝0）describes an ellipse in the p′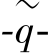
plane，as illustrated in Figure 7.17.The parameter M in Eq.7.54 determines the height of the ellipse.The height of the ellipse is responsible for the ratio of horizontal to vertical stresses in primary one⁃dimensional compression.
As a result，the parameter M determines largely the coefficient of lateral earth pressure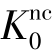 
.In view of this，the value of M can be chosen so that a known value of 
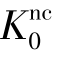is matched in primary one⁃dimensional compression.Such an interpretation and use of M differs from the original critical state line idea，but it ensures a proper matching of 
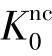.The tops of all ellipses are located on a line with slope M in the p′
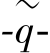plane.In（Burland，1965）and（Burland，1967）the M⁃line is referred to as the critical state line and presents stress states at post peak failure.The parameter M is then based on the critical state friction angle.In the Soft Soil model，however，failure is not necessarily related to critical state.The Mohr⁃Coulomb failure criterion is a function of the strength parametersφand c，which might not correspond to the M⁃line.The isotropic pre⁃consolidation stress pp determines the extent of the ellipse along p′axis.During loading，an infinite number of ellipses may exist（see Figure 7.17），each corresponding to a particular value of pp.In tension（p′＜0），the ellipse extends to ccotφ（Eq.7.55）.In order to make sure that the right hand side of the ellipse（i.e.the‘cap’）will remain in the‘compression’zone（p′⁃0），a minimum value of c cotφis adopted for pp.For c＝0，a minimum value of pp equal to a stress unit is adopted.Hence，there is a threshold ellipse as illustrated in Figure 7.17.
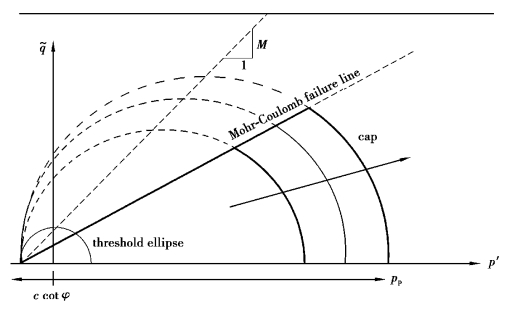
Figure 7.17 Yield surface of the Soft Soil model in p′⁃q～⁃plane
The value of pp is determined by volumetric plastic strain following the hardening relation.This equation reflects the principle that the pre⁃consolidation stress increases exponentially with decreasing volumetric plastic strain（compaction）.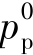
can be regarded as the initial value of the pre⁃consolidation stress，and according to Eq.7.56，the initial volumetric plastic strain is assumed to be zero.
In the Soft Soil model，the yield function，Eq.7.53 describes the irreversible volumetric strain in primary compression，and forms the cap of the yield contour.To model the failure state，a perfectly⁃plastic Mohr⁃Coulomb type yield function is used.This yield function represents a straight line in p′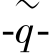
plane as shown in Figure 7.17.The slope of the failure line is smaller than the slope of the M⁃line.The total yield contour，as shown by the bold lines in Figure 7.17，is the boundary of the elastic stress area.The failure line is fixed，but the cap may increase in primary compression.Stress paths within this boundary give only elastic strain increments，whereas stress paths that tend to cross the boundary generally give both elastic and plastic strain increments.
For general states of stress（p′，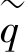
），the plastic behaviour of the Soft Soil model is defined by the combination of the cap yield function and the Mohr⁃Coloumb yield functions.The total yield contour in principal stress space is indicated in Figure 7.18.
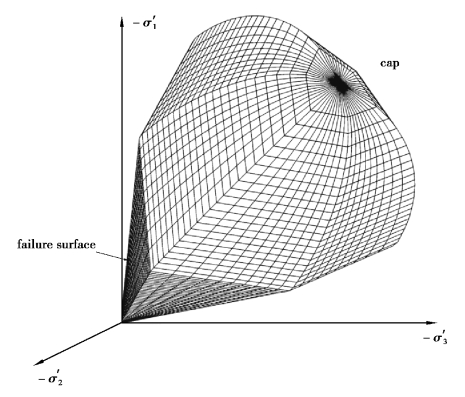
Figure 7.18 Representation of total yield contour of the Soft Soil model in principal stress space