5.3.5 Newly proposed methods
Finno and Roboski（2005），and Roboski and Finno（2006）proposed parallel distributions of settlement and lateral ground movement for deep excavations in soft to medium clays.The parallel distribution profiles were based on optical survey data obtained around a 12.8 m⁃deep excavation in Chicago supported by a flexible sheet pile wall and three levels of anchors.They found that when using the complementary error function（erfc），just geometry and maximum movement parameters are necessary for defining the parallel distributions of ground movement.The complementary erfc function is defined as
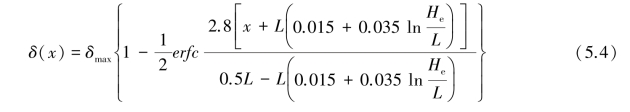
where
δmax can be either maximum settlement or maximum lateral movement；
L is the length of the excavation；
He is the height of the excavation as presented in Figure 5.13.
Although Equation 6.4 was derived from observations of flexible wall excavations，it has been reported by Roboski and Finno（2006）that it can predict with reasonable agreement the ground movement profiles for stiffer walls.
Special attention is needed in excavations where there are larger diameter utility pipes，buildings with stiff floor systems，buildings supported on deep foundations，and deep foundations between the building and the excavation because they provide restraint for the movements and will consequently affect their distribution.Roboski and Finno（2006）concluded that the complementary error function is applicable to excavations where the induced ground movements can develop with little restraint.
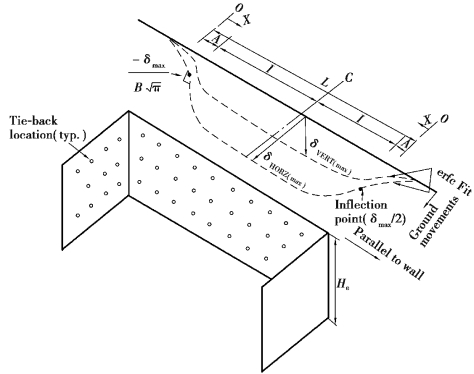
Figure 5.13 Derived Fitting Parameters for the Complementary Error Function.δVERT，settlement；δHORZ，lateral movement（After Roboski and Finno，2006）
Recently，a series of finite element analyses were carried out by Zhang and Goh（2013），and Goh et al.（2017）to investigate the influences of soil properties，wall stiffness，excavation length，excavation depth，clay thickness at the base of the excavation and wall embedment depth，on the maximum wall deflection induced by braced⁃excavation in clay.Some advanced computational learning tools such as multivariate adaptive regression splines（MARS）and logarithmic regression model were used to estimate the simple wall deflection equation.As for 2D cases，a simple logarithmic regression model was developed for estimatingδHm in terms ofα，cu，He，D，L／B and D／B，as shown in Eq.5.5.Meanwhile，the optimal MARS models was also developed based on a total of 1，120 cases to determine the maximum diaphragm wall deflection；the ANOVA parameter relative importance assessment indicates that the two variables which contribute most to the diaphragm wall deflection are h（excavation depth）and B（excavation width）.The BFs（basic functions）and their corresponding equations for the optimal MARS model is tabulated in Table 5.1 and the interpretable MARS model is given by Eq.5.6.
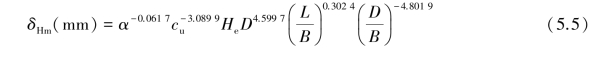
where
αrepresents walls with different rigidities，a smallerα＝0.1 represents flexible walls and largerαrepresents stiff walls；
cu is the undrained shear strength of the soil；
He is the excavation depth；
D is the wall penetration depth；
Table 5.1 Basis functions and corresponding equations of MARS model for diaphragm wall deflection prediction
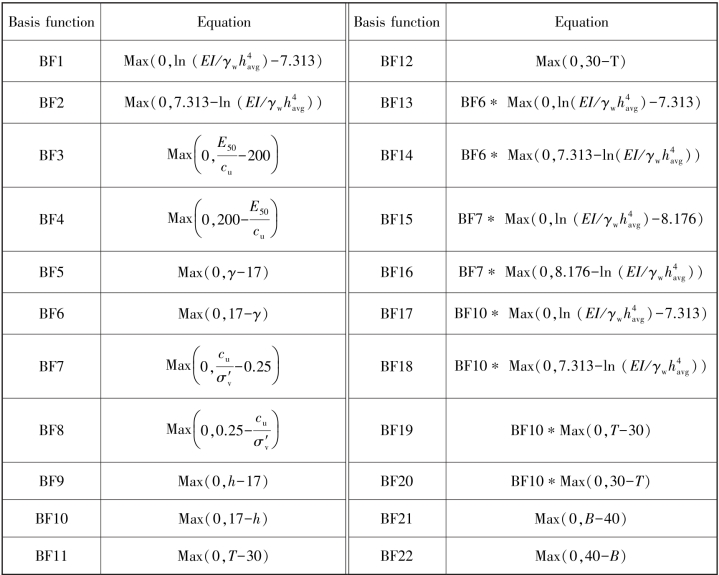
Note：EI is the wall stiffness；havg is the average vertical distance；h is excavation depth；B is excavation width；γis soil unit weight；T is soft clay thickness；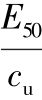
is soil stiffness；
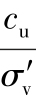is soil shear strength ratio.
L and B are excavation length and width respectively.δh0＝165－50.889×BF1＋66.598×BF2－0.191 4×BF3＋0.495 6×BF4－10.324×BF5＋19.135×BF6－326.34×BF7＋815.69BF8＋4.998 1×BF9－6.189 1×BF10＋7.4897×BF11－7.0073×BF12－13.712×BF13＋24.131×BF14＋540.93×BF15－331.28×BF16＋2.771 6×BF17－4.582 1×BF18－1.1808×BF19＋0.861 2×BF20＋0.511 4×BF21－1.547 4×BF22（5.6）