5.2.2 Excavation in front of wall
For any given applied loading conditions(actions)behind an embedded retaining wall,ground movements arising from excavation in front of the wall are influenced by:
a.stress changes due to wall installation and excavation.
b.excavation geometry.
c.ground stiffness and strength.
d.changes in groundwater conditions.
e.type and stiffness of the wall and its support system.
f.construction sequence and methods.
g.quality of workmanship.
Although any one of these factors may control the overall movement of a supported excavation,the interaction between these factors in the actural three dimensions(3D)makes the problem even more complicated.For this reason and the fact that it is impossible to quantify many of these factors,structural modelling and analysis of excavation support systems seldom results in reliable prediction of movement.So,the estimation of ground movements associated with supported excavations is generally based on a combination of empirical and analytical methods in conjunction with the application of sound judgment and experience.
However,before considering in detail how such estimates can be made quantitatively,it is appropriate to first consider each of these factors in more detail.
1)Stress changes due to wall installation and excavation
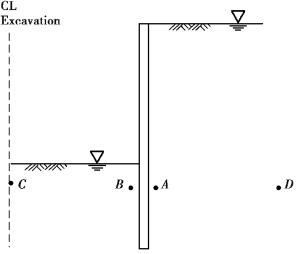
The complexity of stress changes at four locations beneath,adjacent to and remote from an excavation in an overconsolidated clay supported by a diaphragm wall during excavation is illustrated in Box 5.1.
As can be seen from the stress path in Box 5.1,the proximity of element B to the failure envelope is the most significant factor that influences the horizontal movement of the soil below excavation level.Yield will be small,and both heave and horizontal movements will also be small if stress path 2 to 4 is well within the passive failure envelope.If the effective stress points for element B are close to the failure envelope,this is indicative of significant yield and local passive failure resulting in relatively high magnitude lateral movements.
Box 5.1 Stress paths for soil elements near an excavation retained by a cast in situ embedded wall in overconsolidated clay
It is assumed that pore water pressures are initially hydrostatic below an in situ groundwater level.After excavation,steady⁃state seepage eventually develops from the initial groundwater level behind the wall to a groundwater level at formation level in front.
The geological stress history of the clay comprises deposition followed by the removal of overburden,resulting in an overconsolidated material withσ′h>σ′v in situ.This is represented on the indicative stress path 0′⁃0 in the figure.There may also be reloading by superficial deposits,which is not shown with figure.
During wall installation,both elements A and B will be subjected to a reduction in lateral total stress as the excavation is made under support fluid,followed by an increase in lateral total stress as the concrete is poured(assuming uncased bores or panels).Field measurements(Symons and Carder,1992)and centrifuge model tests(Powrie and Kantartzi,1996)show that pore water pressures will fall during excavation under bentonite and recover to approximately their in situ values during concreting.Indicative effective stress paths are shown in the figure(0⁃1 under bentonite,1⁃2 during concreting).
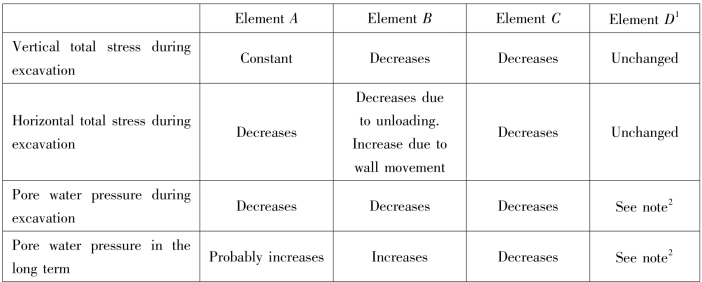
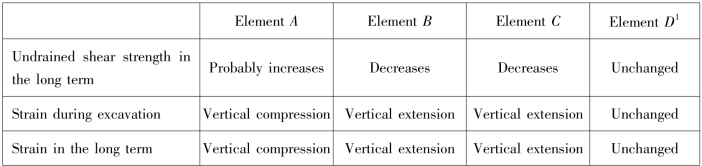
During excavation in front of the wall,the wall is likely to move forward into the excavation resulting in a reduction in horizontal total stress for element A behind the wall.This will cause a reduction in pore water pressure behind the wall.In an overconsolidated clay,shear following yield will also generate negative excess pore water pressures(2⁃3 in the figure).The long⁃term steady⁃state seepage pore water pressure behind the wall is less than the initial in situ hydrostatic value,but probably greater than the pore water pressure immediately following excavation so that the pore water pressure will probably increase in the long term as steady state conditions are approached(3⁃4).Overall(2⁃4)element A will experience a reduction in pore water pressure and a reduction in horizontal total stress at constant vertical total stress.These changed in pore water pressures and boundary stresses will result in an increase in vertical effective stress and a decrease in horizontal effective stress,bringing element A towards the active condition.
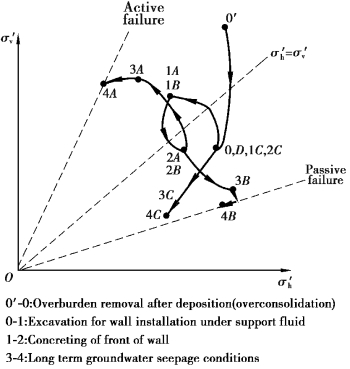
During excavation,element B will experience a large reduction in vertical total stress,which will result in a large reduction in pore water pressure.Movement of the wall below formation level into the soil in front tend to increase the horizontal total stress.These changes are likely to result in an increase in horizontal effective stress and a reduction in vertical effective stress during excavation(2⁃3 in the figure).In the long term,pore water pressure will increase again as steady state seepage develops,reducing both vertical and horizontal effective stress and bringing the soil towards passive failure(3⁃4).
These changes in stress from the initial stage prior to excavation are summarized in the table:
continued
Notes:1.Assumed to be located sufficiently remotely from the wall so as not to be affected by changes in soil stress due to excavation in front of the wall.
2.Depends on ground permeability.
2)Excavation geometry
The geometrical shape and area in plan and the excavation depth all have a critical influence on the magnitude and distribution of ground movements around an excavation in any given ground conditions.In many situations,embedded retaining walls form a closed box,or a more complex shape.In such cases,the distribution of movement will be complex and its magnitude is difficult to estimate without the benefit of comparable experience.The corners of an excavation tend to restrict movement.
Analyses undertaken to date allowing for D effects are site specific and the extrapolation of the results of such studies for general application is limited only to reasonably comparable situations.Further work is necessary before reliable correlations can be established for general application.However,St John(1975)found that plane strain and axi⁃symmetric analyses gave similar vertical movements.Horizontal movements from the axi⁃symmetric analysis were some 50 percent of those computed in the plane strain model.Simic and French(1998)found that steel quantities in diaphragm wall reinforcement could be reduced by about 25 percent at the corners of the excavation they studied.Temporary prop loads measured across the corners of the Mayfair car park excavation in London indicate a 40 percent reduction within a horizontal distance from the corner equal to the excavation depth,compared to the central props where plane strain conditions predominated(Richards et al.,1999).Being significantly economical are possible.
In addition,the effects of the existence of a corner on the deflection behavior of an excavation wall as represented by the 3D response of excavations have been reported in the literature by a number of researchers,namely,Ou et al.(1996,2000),Chew et al.(1997),Lee et al.(1998),Finno and Roboski(2005),Roboski and Finno(2006),Finno et al.(2007)For a typical rectangular shaped excavation,Ou et al.(1996)defined the plane strain ratio(PSR)as the maximum lateral wall displacement computed from the results of 3D analysis normalized by that derived from a plane strain analysis.Finno et al.(2007)extended this work and based on field and parametric numerical studies,concluded that the PSR for excavations in clays was strongly influenced by the ratio of the length of the excavation in relation to its width(L/B)and the ratio of the length of wall to the excavation depth(L/H).Their findings are presented in Figure 5.3 and show that PSR is less than 1 for L/B and L/H ratios of less than 2 and 6 respectively.In general,greater corner effects are observed for relatively deep excavations(as evidenced by small L/H ratios).That is,for any given geometry,higher reductions in movements occur near the corners of deep excavations as compared to shallower excavations in similar soil conditions with similar support systems.When L/H is larger than 6,plane strain and 3D analyses yield similar wall movements along the perimeter wall at the center of the excavation.
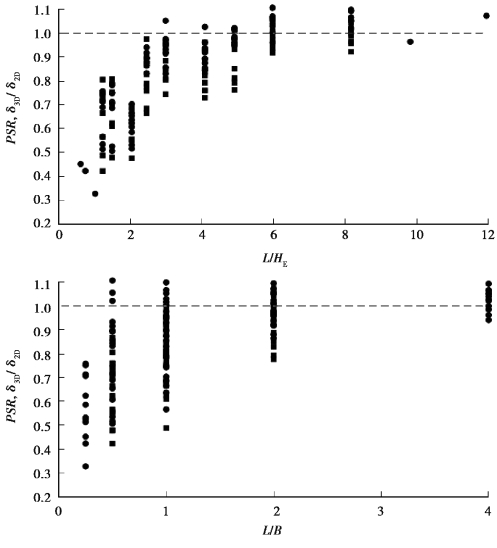
Figure 5.3 Relationship between PSR and excavation geometry(Finno,2007)
3)Ground stiffness and strength
Overall ground movements(heave beneath the excavation,wall deflections and ground movements around the excavation)are strongly influenced by the stiffness of the ground and in weaker ground soil strength.Movements in competent ground conditions,such as dense coarse⁃grained soils,stiff clays and weak rocks are generally much smaller than in less competent ground conditions,such as soft and firm clays and loose sands.Soft and firm clays can be susceptible to large movements even at small excavation depths,owing to the potential for undrained bearing capacity failure at the toe of the wall.The requirement that the difference in vertical stress in the soil on either side of the wall at the toe should not exceed the bearing capacity of the soil gives a theoretical upper limit to the excavation depth,irrespective of the nature of the support system provided.
4)Changes in groundwater condition
If the retaining wall does not provide a hydraulic cut⁃off at depth,a steady⁃state groundwater seepage condition will develop involving flow around the toe of an impermeable retaining wall and subsequently upwards to the excavation formation level.Unless recharged from another source,such groundwater flow will result in drawdown behind the wall(and related decreased pore water pressures)and reduced pore water pressures within the excavation compared to the initial hydrostatic condition.Establishment of a steady⁃state groundwater flow regime may result in both vertical ground movements,owing to the consolidation or swelling of fine⁃grained soils,and horizontal ground movements associated with the lateral movement of the wall into the excavation.
More sources of ground movements potentially arising from groundwater flow are considered in Section 5.2.3.
5)Type and stiffness of the wall and its support system
The type of wall selected and the excavation construction method are major influences on the magnitudes of wall and ground movements.It is well known that stiffer walls attract larger bending moments than more flexible walls with the same ground and support conditions(Rowe et al.,1952).Wall flexure redistributes the stresses imposed by the soil away from the linear,limit equilibrium ideal,which reduces the structural stress resultants,but at the expense of larger wall and ground movements.For a propped or anchored embedded wall of given overall height H and flexural stiffness EI,bending effects are most significant when the wall is supported at the top.In general,wall defor⁃mation occurs partly due to rigid body rotation(in the case of a propped or anchored wall,about the position of the prop or anchor),and partly due to bending(Figure 5.4).
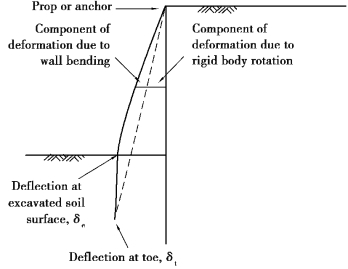
Figure 5.4 Component of wall displacements and definition of a stiff wall
The relative importance of wall movement resulting from bending and rigid body rotation may be characterized by means of a dimensionless flexibility number R,given by:
![]()
where
G∗is the rate of increase in soil shear modulus with depth in kN/m3.
H is the total height of the wall in m.
EI is the flexural stiffness of the wall,in kN·m2/m.
Diakoumi et al.(2013)show that,depending on the soil strength and groundwater conditions,wall flexibility effects will reduce bending moments in an embedded wall propped at the crest to below those calculated using an EC7⁃1 type limit equilibrium linear stress distribution at values of log10R between 1.5 and 2.5(R between 32 and 320)(see Figure 5.5).
For multi⁃propped walls,Addenbrooke et al.(2000)define displacement flexibility(in kN/m4)Δas:
![]()
where
h is the average vertical prop spacing of a multi⁃propped support system.
By keepingΔconstant,a designer can consider different wall types and associated propping systems for the same absolute displacement.This can be useful when comparing value engineer alternatives to satisfy particular deformation performance requirements alternatively for multi⁃propped walls,Clough et al.(1989)and Clough and O Rourke(1990)defined dimensionless system stiffnessρs as
![]()
where
γw is the unit weight of water.
ρs may be used in conjunction with the FoS against base failure to provide an initial“first Pass”estimate of likely maximum wall movements for an excavation of given depth(see Figure 5.4)where
•good workmanship and tight construction control have been employed.
•the ground is not subject to consolidation effects.
•the initial cantilever stage wall deflection is a relatively small component of the total movement.
Such an initial estimate will not allow for other significant factors(previously discussed),which may strongly influence wall deflection.It is evident from Figure 5.5 that in this circumstance and with good quality workmanship and well⁃controlled construction practice,wall deformation due to excavation should be relatively insensitive to the magnitude of system stiffness.This means that with adequate propping,flexible walls(e.g.sheet pile walls)embedded in stiff clays and other adopted without significant increase in ground movements.
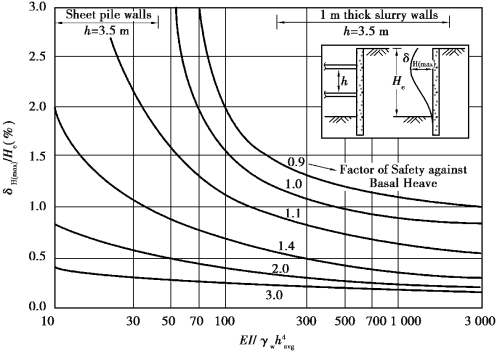
Figure 5.5 Maximum lateral wall movements vs.system stiffness(After Clough et al.,1989)
As for multi⁃propped excavation,the prop or strut properties also have significant influence on wall movement.As shown in Figure 5.6(a),with the start of the first stage of excavation,wall movement will be produced and form a cantilever shape.The second stage of excavation starts after the installation of the first level of struts.If the stiffness of the struts is high enough,the compression of the struts will be rather small,so that the retaining wall will rotate about the contact point between the struts and the wall,and wall deformation is thus generated.The maximum wall deformation will occur near the excavation surface as shown in Figure 5.6(b).With the completion of the second level of struts,the third stage of excavation starts.Suppose the stiffness of the second level of struts is also strong enough,the retaining wall will continue rotating about the contact point with the second level of the struts,and wall deflection is produced again.The location of the maximum deformation will be near the excavation surface[Figure 5.6(c)].If the soil below the excavation surface is soft soil,the resisting force to prevent the retaining wall from pushing in will be weak and the location of the maximum deformation will be mostly below the excavation surface.Inferred from the same extrapolation,excavation in stiff soils(such as sand)will mostly produce the maximum deformation above the excavation surface.Actually,the locations of the maximum deformations are found near the excavation surfaces in most of the excavations in Taipei(Ou et al.,1993).
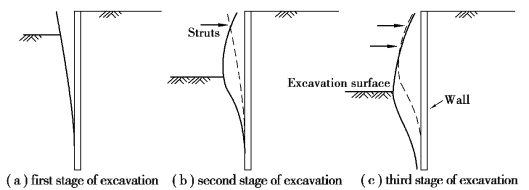
Figure 5.6 Relationship between the shape of wall deformation and high strut stiffness
The problem of strut spacing can be distinguished into that of horizontal spacing and vertical spacing.Narrowing the horizontal spacing can increase the stiffness of the struts per unit width.The effect will be the same as increasing the stiffness of the struts.Shortening the vertical spacing of struts can effectively decrease the deformation of a retaining wall because the stiffness of the strut system is raised.The stiffness raised,and the deformation of a retaining wall declines.Put another way,since the deformation of a retaining wall is the accumulated result throughout all the excavation stages,with the unsupported length generated in each stage being reduced due to the shortening of the vertical spacing,the deformation of a retaining wall will decline as a result.The“unsupported length”refers to the distance between the lowest level of strut and the excavation surface.
When applying the braced excavation method(or the anchored excavation method),preload is often exerted onto struts.Suppose the struts are placed at shallower levels.Thus,under normal conditions(with the preload not too small),the preload will be capable of pushing the retaining wall out.If the struts are placed at deeper levels,with the earth pressure growing with the depth,the preload of struts will not be able to push the wall outward easily(Ou et al.,1998).Actually,whether the preload is capable of causing a retaining wall to move,preload is always helpful to reduce the displacement of a retaining wall or the ground settlement.
6)Construction sequence and methods
The choice of wall type and its installation,and the overall excavation construction sequence and duration significantly influence ground movements around an excavation for any given ground and groundwater conditions;excavation geometry and dimensions construction sequence(e.g.top⁃down versus bottom⁃up)appropriate for particular circumstances is provided in Gaba et al.(2017)where the respective advantages and disadvantages of each approach are discussed in detail.It is generally assumed that the top⁃down construction method helps to minimize ground movements because this applies early stiff support(typically via a structural slab)near the top of the wall ahead of any significant excavation in front of the wall.However,the regularity of support provided by subsequent floors at each storey height of the structure may not necessarily provide support to the wall at optimum levels(e.g.where external surcharge loading may be applied adjacent to the excavation from existing foundations,or where lateral support to the wall may be referable at locations other than where the structural slabs are located due to,for example,the need to minimize the vertical height from the penultimate support to excavation formation level where weak strata exist immediately below final formation level).CGS(2006)reports that movements of anchored walls can be less than those that are supported struts for the following reasons:
①Anchors can be stressed to a proportion of the design load to the completed excavation before excavation below the anchors level.
②Typically,little excavation occurs below the anchor level to enable anchor installation equipment to operate.
③The connection between struts,waler beams and the wall is often imperfect and without significantly pre⁃loading the struts;compression of these connections can lead to additional deformation.
④When completing the structures within the excavation by the bottom⁃up method,struts are typically removed but anchors can be left in place for longer duration,if required.7)Quality of workmanship
Not surprisingly,unprofessional or inappropriate attitudes or failure to effectively apply risk management and mitigation measures on site in routine good construction practice,or not to adhere to recognized good workmanship standards can lead to uncontrolled ground movements and even local failure and progressive collapse.In this regard,according to Puller(2003),there are numerous examples of poor site practices such as:
①late installation of supports.
②unplanned over⁃excavation.
③poor pile driving and caisson construction.
④water seepage and loss of ground through holes for tie backs and at joints or sheet pile interlocks or diaphragm wall joints.
⑤remoulding and undercutting of clay berms.
⑥excessive surcharge loads from spoil heaps and construction equipment.
⑦lack of rigidity and tightness of shores and braces.
⑧control of ground movements.
Ground movements are best minimized and controlled at source.In this regard,measures that can be adopted by varying the construction sequence and methods while maintaining a good standard of workmanship.Measures that can be adopted to minimize ground movements around and beneath an excavation are summarized here:
•Good workmanship is essential.Supports should be installed tight to the wall.The prop,and any packing between the prop and waling,should not rely on friction or adhesion between the prop end and waling to hold it in place.
•The wall should have adequate embedment in competent(stiff)strata for satisfactory vertical and lateral stability.
•Minimize the first⁃stage excavation and install the first(stiff)support as early as possible in the construction sequence.With a high stiffness prop installed early during excavation,the horizontal wall movement is not likely to be measured at the wall top,but a depth of some 0.7 to 0.9 times the maximum excavation depth(Carder,1995).
•Minimize the extent of the dig beyond the proposed support levels.
•Minimize delays to the construction of the wall and its support system.
•Prevent deterioration of lateral support from a clay berm by blinding it or covering it with a waterproof membrane to maintain the berms natural moisture content.
•Avoid unplanned over⁃excavation.
•Minimize removal of fines during dewatering and loss of fines through wall joints.
•Minimize drawdown outside excavation.
