7.4.1 Describing Small⁃strain stiffness with a sim...
In soil dynamics，small⁃strain stiffness has been a well⁃known phenomenon for a long time.In static analysis，the findings from soil dynamics have long been considered not to be applicable.
Seeming differences between static and dynamic soil stiffness have been attributed to the nature of loading（e.g.inertia forces and strain rate effects）rather than to the magnitude of applied strain which is generally small in dynamic conditions（earthquakes excluded）.As inertia forces and strain rate have only little influence on the initial soil stiffness，dynamic soil stiffness and small⁃strain stiffness can in fact be considered as synonyms.Probably the most frequently used model in soil dynamics is the Hardin⁃Drnevich relationship.From test data，sufficient agreement is found that the stress⁃strain curve for small strains can be adequately described by a simple hyperbolic law.The following analogy to the hyperbolic law for larger strains by Kondner（1963）was proposed by Hardin Drnevich（1972）：
where the threshold shear strainγr is quantified as
with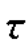 
max being the shear stress at failure.Essentially，Eqs.7.30 and 7.31 relate large（failure）strains to small⁃strain properties which often work well.
More straightforward and less prone to error is the use of a smaller threshold shear strain.Santos＆Correia（2001），for example suggest to use the shear strainγr＝γ0.7，at which the secant shear modulus Gs is reduced to about 70 of its initial value.Eq.7.30 then is rewritten as
where a＝0.385.
In fact，using a＝0.385 andγ＝γ0.7 gives Gs／G0＝0.722.Hence，the formulation“about 70%”should be interpreted more accurately as 72.2%.
Figure 7.10 shows the fit of the modified Hardin⁃Drnevich relationship（Eq.7.30）to normalised test data.
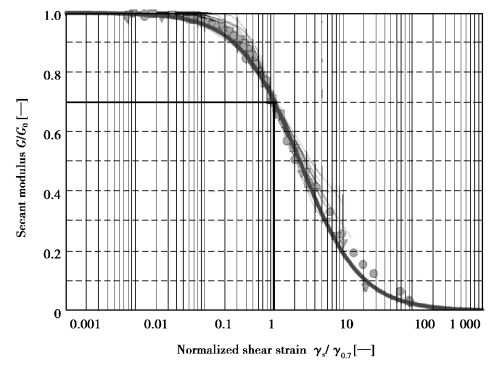
Figure 7.10 Results from the Hardin⁃Drnevich relationship compared to test data by Santos＆Correia（2001）