12.3.1 Gradient⁃based method
The gradient method is probably one of the oldest optimization algorithms，going back to 1847 with the initial work of Cauchy.The gradient method is an algorithm for examining the directions defined by the gradient of a function at the current point.Based on the basic principle，different gradient⁃based methods have been developed，such as the steepest descent method，the conjugate gradient method，the Levenberg⁃Marquardt method，the Newton method and several Quasi⁃Newton methods，the Davidon⁃Fletcher⁃Powell，and the Broyden⁃Fletcher⁃Goldfarb⁃Shanno methods.
A rapid convergence is the primary advantage of a gradient⁃based method.Clearly，the effective use of gradient information can significantly enhance the speed of convergence compared to a method that does not compute gradients.However，gradient⁃based methods have some limitations，being strongly dependent on user skills（e.g.，the basic knowledge of typical values of parameters and the ability of selecting ranges of parameters），due to the need to choose the initial trial solutions.Also，they can easily fall into local minimums，mainly when the procedure is applied to multi⁃objective functions，as it is the case for material parameter identification with a nonlinear soil model.The requirement of derivative calculations makes these methods nontrivial to implement.Another potential weakness of the gradient⁃based methods is that they are relatively sensitive to difficulties such as noisy objective function spaces，inaccurate gradients，categorical variables，and topology optimization.
1）Steepest descent algorithm
To characterize the discrepancy between the experimental behavior and the modelled one，a scalar error function，Ferr can be defined by using the least⁃square method（Levasseur，2008）：
where N is the number of observation，ui is the ith observed value，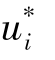
is the computed value and 1／Δui is the weight of the discrepancy between ui and 
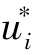.Basically，1／Δui can be decomposed into two parts：
whereεis an absolute error andαa dimensionless relative error.Depending on the physical meaning of the experimental data，εandαallow to give more or less weight to measured points.Ifεis equal to zero，the points with weak measured values have more weight.The sensitivity of the parameters which influence these points is well taken into account by Ferr.On the contrary，whenαis equal to zero，all the points of the curve have the same weight.Δui is directly linked to measurement errors，which is similar to the discrepancy norm usually used in the literature.
The error function Ferr（p）is defined as a scalar for each set of Np unknown parameters，which is noted as a vector p.The inverse problem is then solved as a minimization problem in the Np⁃dimension space（the search space）restricted to authorized values of p between pmin and pmax by using the steepest descent algorithm
Step 1：Given an a priori set
Step 2：The next set of unknown parameters pi＋1 is then chosen such that
Where di is a vector indicating the downward direction
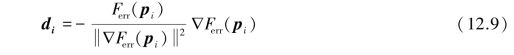
and x is a non⁃dimensional scalar step of which the optimum value is determined by a quadratic estimation of Ferr in the di direction.
Step 3：The optimization program starts again from Stage 1 until Ferr is less than the experimental measured error or until the norm of the incremental parameter vector，
is less than the expected precision on the parameter values.
This algorithm corresponds to the traditional steepest descent method which is the simplest gradient method.
2）Gauss⁃Newton method
Finno used UCODE（Poeter and Hill 1998），a computer code designed to allow inverse modeling posed as a parameter estimation problem，to conduct the back analysis.The model independency allows the chosen numerical code to be used as a separate entity wherein modifications only involve model input values，allowing one to develop a procedure that can be easily employed in practice and in which the engineer will not be asked to use a particular finite element code or inversion algorithm.Rather，macros can be written in a Windows environment to couple UCODE with any finite element software.
With the results of a finite element prediction in hand，the computed results are compared with field observations in terms of an objective function.In UCODE，the weighted least⁃squares objective function S（b）is expressed as
where
b＝vector containing values of the parameters to be estimated；
y＝vector of the observations being matched by the regression；
y′（b）＝vector of the computed values which correspond to observations；
ω＝weight matrix wherein the weight of every observation is taken as the inverse of its error variance；
e＝vector of residuals.
A sensitivity matrix，X is then computed by using a forward difference approximation based on the changes in the computed solution due to slight perturbations of the estimated parameter values.This step requires multiple runs of the finite element code.Regression analysis of this nonlinear problem is used to find the values of the parameters that result in a best fit between the computed and observed values.In UCODE，this fitting is accomplished with the modified Gauss⁃Newton method，the results of which allow the parameters to be updated by using
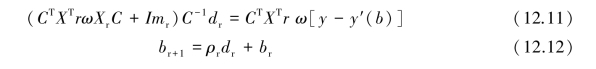
where
dr＝vector used to update the parameter estimates b；
r＝parameter estimation iteration number；
Xr＝sensitivity matrix Xij＝∂yi／∂bi evaluated at parameter estimate br；
C＝diagonal scaling matrix with elements cjj equal to 1／（XTrωXr）jj；
I＝identity matrix；
mr＝Marquardt parameter（Marquardt 1963）used to improve regression performance；
ρr＝damping parameter，computed as the change in consecutive estimates of a parameter normalized by its initial value，but it is restricted to values less than 0.5.
In Finno's（2005）study，mr is initially set equal to 0 for each parameter estimation iteration r.For iterations in which the vector d defines parameter changes that are unlikely to reduce the value of the objective function，as determined by the Cooley and Naff（1990）condition，mr is increased by 1.5 mr（old）＋0.001 until the condition is no longer met.
At a given iteration，after performing the modified Gauss⁃Newton optimization，decide whether the updated model is optimized according to either of two convergence criteria：
a.The maximum parameter change of a given iteration is less than a user⁃defined percentage of the value of the parameter at the previous iteration；or
b.The objective function，S（b）changes less than a user⁃defined amount for three consecutive iterations.
After the model is optimized，the final set of input parameters is used to run the finite element model one last time and produce the“updated”prediction of future performance.
The relative importance of the input parameters being simultaneously estimated can be defined by using various parameter statistics（Hill，1998）.The statistics found most useful for this work are the composite scaled sensitivity，ccsj，and correlation coefficient，cor（i，j）.The value of ccsj indicates the total amount of information provided by the observations for the estimation of parameter j，and is defined as
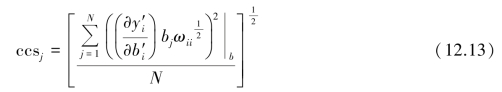
where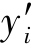 
＝ith computed value；bj＝jth estimated parameter；∂y′i／∂b′i＝sensitivity of the ith computed value with respect to the jth parameter；ωii＝weight of the ith observation；and N＝number of observation.
The values of cor（i，j）indicate the correlation between the ith and jth parameters，and are defined as
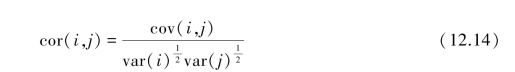
where cor（i，j）＝off⁃diagonal elements of the variance⁃covariance matrix V（b′）＝s2（XTrωXr）－1 in which s2＝model error variance；var（i）and var（j）refer to the diagonal elements of V（b′）.
Inverse analysis algorithms allow the simultaneous calibration of multiple input parameters.However，identifying the important parameters to include in the inverse analysis can be problematic，and it is generally not possible to use a regression analysis to estimate every input parameter of a given simulation.The number and type of input parameters that one can expect to estimate simultaneously depend on a number of factors，including the soil models used，the stress conditions of the simulated system，available observations，and numerical implementation issues.Note that within the context of finite element simulations，individual entries within element stiffness matrices may depend on combinations of soil parameters，implying that more than one combination of these parameters can yield the same result.Consequently，these parameters will be correlated within the context of the optimization solution，even though the parameters may be independent of a geotechnical perspective.
The total number of input parameters can be reduced in three steps to the number of parameters that are likely to be optimized successfully by inverse analysis.
In Step 1，the number of relevant and uncorrelated parameters of the constitutive model chosen to simulate the soil behavior is determined.The number of parameters that can be estimated by inverse analysis depends upon the characteristics of the model，the type of observations available，and the stress conditions in the soil.Composite scaled sensitivity values（Eq.12.13）can provide valuable information on the relative importance of the different input parameters of a given model.Parameter correlation coefficients（Eq.12.14）can be used to evaluate which parameters are correlated and are，therefore，not likely to be estimated simultaneously by inverse analysis.
In Step 2，the number of soil layers to calibrate and the type of soil model used to simulate the layers determine the total number of relevant parameters of the simulation.An additional sensitivity analysis may be necessary to be checked for correlations between parameters relative to different layers.
Finally，in Step 3，the total number of observations available and computational time considerations may prompt a final reduction of the number of parameters to optimize simultaneously.A detailed example of this procedure is presented by（Calvello and Finno，2004）.
The relative fit improvement，RFI，which indicates by what percentage the optimized results improved compared to the predictions at the beginning of a certain stage，can be used to quantify the effectiveness of optimization procedure and the reliability of the predictions.RFI is defined as：
where S（b）in＿i—initial value of the objective function is at stage i；and S（b）fin＿i—optimized value of the objective function is at the end of stage i.
The error variance s2，a commonly used indicator of the overall magnitude of the weighted residuals，is computed as
where S（b）＝objective function；ND＝number of observations；and NP＝number of estimated parameters.
3）quasi⁃Newton method
Tang et al.（2008）employed an objective function f（x）defined as
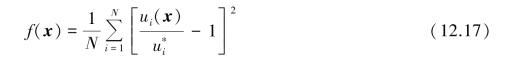
where N＝number of observations；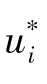
is the measured values；ui（x）is the computed values；x is the selected parameter vector.
Then，specify an initial set of target variables x0，and then these variables are updated iteratively in the optimization analysis process.The iterative procedure used in this study can be expressed as
where k is the iteration number and S is a search direction.The step size in terms of the scalar quantityαk defines the moving distance in the search direction S.Use of Eq.12.18 consists of two major components：the first is to determine the search direction Sk，and the second is to calculate aαk with which the minimized f（x）can be obtained in the determined search direction Sk.The second component is also called line search.The detailed procedures are described as follows：
（a）Compute the search direction Sk.
（b）Determine the optimum step sizeαk so that f（xk＋αkSk）is the minimum value in the search direction.
（c）Let xk＋1＝xk＋αkSk where xk＋1 are new and xk old parameter vectors，respectively.
（d）Repeat（1）to（3）until convergence is reached.
The difficulty in solving highly nonlinear Eq.12.17 is expected，and thus this study employs quadratic Taylor series approximation at kth iteration to solve this equation，which can be expressed as whereδx＝xk＋1－xk and H（xk）is the Hessian matrix，which denotes the matrix of second partial derivatives of the objective function with respect to the target variables.
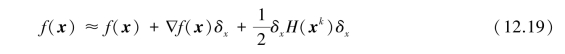
By incorporating the stationary condition▽f（xk）＝0 into Eq.12.19，the following equation can be obtained：
By comparing Eq.12.20 with Eq.12.18，whenα∗＝1，the Sk can be expressed as
Eq.12.21 is the well⁃known Newton method and can be used to determine the search direction Sk.In theory，only one step computation is required to reach the minimum of f（x）when f（x）is a quadratic.However，since f（x）in Eq.12.17 is not a quadratic，it is necessary to invert the matrix H（xk）to compute the second partial derivatives of f（x），in which one iteration requires n（n＋1）／2 differentiations of the objective function（n is the number of variables）.Note that such iterative process in the back analysis is cumbersome and time⁃consuming.Therefore，for upgrading the efficiency of computation，the quasi⁃Newton method is incorporated in the present study instead of the Newton method.To this end，the quasi⁃Newton method，BFGS（Broyden⁃Fletcher⁃Goldfarb⁃Shanno）method（Fletcher，1980）is adopted and expressed as
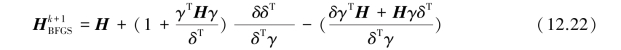
whereγk＝▽f（xk＋1）－▽f（xk）andδk＝xk＋1－xk＝αkSk.Note that，for clarity，the sign of the kth iteration on the right hand side of this equation is omitted.
In addition，the combination of the DSC（Davies⁃Swann⁃Campey）method（Himmelblau，1986）and the Powell's（1962）quadratic interpolation（PQI）method is employed in this study to determine the optimum step size.Details of this method can be referred to Himmelblau（1986）.
Next，the principle of the convergence criterion for determining when the process of the back analysis should be terminated is based on whether one of the three components of the convergence criterion is reached at two successive iterations.The three components are expressed as
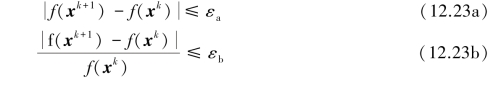
whereεa，εb andεc are tolerances.
The first component of the convergence criterion（Eq.12.23a）is based on the consideration that if the absolute value of change of the objective function obtained between two successive iterations is less than the specified（user⁃defined）tolerance.The percentage of the change of the objective function is employed as the second component（Eq.12.23b）to judge if the convergence is reached.Finally，the percentage of change of target parameters is used as the third component（Eq.12.23c）.When one of three components of the convergence criterion is satisfied at two successive iterations，the optimization analysis is terminated because the next effective search direction cannot be found.Conversely，if none of the three components is satisfied，the optimized search direction can be determined and the analysis proceeds to search the step size.
The PQI method is incorporated in the developed NOT to effectively compute the optimized step size.Specifically，the convergence criterion of the step size consists of two components：
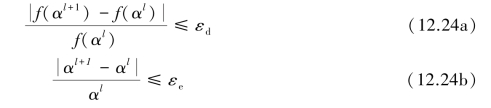
where l is iteration number of line search；αl andαl＋1 are the optimum step sizes computed at lth and（l＋1）th iterations，respectively；f（αl）and f（αl＋1）are the objective function at lth and（l＋1）th iterations accordingly.Tang et al.（2008）adoptedεa＝εb＝εc＝0.01 andεd＝εe＝0.001 as the tolerances of converge.
To enhance convergence rate of the optimization analysis，three auxiliary techniques are employed.
（1）Scaling
The convergence rate decreases when orders of magnitude of variables are not identical.Vanderplaats（1984）suggested that each variable can be multiplied by a scaling factor and then solved by the optimization method.As illustrated in Figure 12.3（a），many iterations are required to search the minimum value for the elliptic shape of contours of the objective function defined by the unscaled variables.However，the objective function with scaled variables exhibits a circular shape of contours，and only one iteration is required to obtain the minimum value［see Figure 12.3（b）］.The mathematical formulas are expressed as follows：
where x and x are the original and scaled vectors of variables，respectively.▽f（x）and
are the original and scaled vectors of gradient，respectively.D＝
，x1，x2，…，xn are values of variables for each iteration.
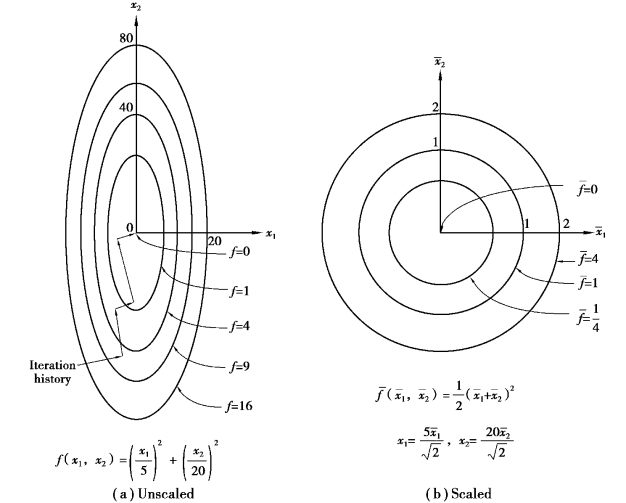
Figure 12.3 Contours of objective function with scaled and unscaled variable（Tang et al.，2008）
（2）Restarting
Since the quasi⁃Newton method employs the current Hessian matrix to update the matrix at the next iteration，both the iteration process and digital computers may cause the problem of error accumulation.Search direction，as obtained from this method，may no longer be the direction of minimum value after a great number of iterations.To deal with this problem，a negative gradient ascent based on a new point after a certain number of iterations is used as the new search direction，instead of using the previously calculated direction.This action is called“restarting”.In this study，restarting is activated when the minimum value of the search direction does not cause the value of the objective function to decrease.
（3）Assurance
Although the PQI method is an efficient way to obtain the optimum step size in a certain search direction，numerical instability may occasionally occur during the iteration process because the objective function formed by various variables is assumed to be a unimodality function.In reality，the type of the function is unknown before iteration begins.Thus，it is not easy to obtain the minimum objective function through the interpolation method.Therefore，this study employs the DSC method to determine three equal step sizes，which can generate a concave curve formed by corresponding objective functions at the beginning of searching the step size.The optimum step size can then be determined by using the PQI method and thus a higher stability and accuracy of results of optimization analyses can be obtained.
Since soil parameters are implicitly included in the objective function，it is difficult to determine the gradient vector of the objective function.To this end，this study adopts the FDM to obtain the gradient vector by
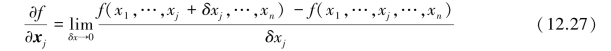
where xj is the jth variable at variable vector.
For the FDM，the value ofδxj essentially has a significant effect on the analysis result.An improper value ofδxj usually causes a large numerical error.Dennis and Schnabel（1983）suggested thatδxj can be determined by whereεm is the machine error.Tang et al.（2007）adoptδxj＝9.77×10－4xj so thatδxj is varied with each iteration.
4）Limitation of gradient⁃based method
Tang et al.（2008）studied the applicability of the gradient⁃based methods.It is found that gradient⁃based method performs well when only one parameter is adopted in the back analysis.However，the further examination indicates the methods are not capable of optimizing a set of parameters.
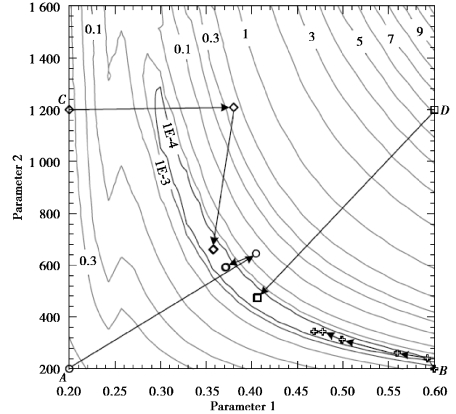
Figure 12.4 Contours of the objective function and identification iteration paths simultaneously using two target parameters（after Tang et al.，2008）
Figure 12.4 shows the identification iteration paths for the four initial values and the contour of the objective function of a hypothetical case，where the exact value of the parameters is（0.35，700）.
The four identification iteration paths fall into the“parabolic⁃pattern valley”，where the value of the objective function is less than 10－4.Theoretically，any point within the valley can be regarded as a solution when the criterion of objective function equal to 10－4 is adopted，causing the back analysis does not yield a unique solution under different initial values.Thus，it should be noted that those optimized soil parameters are one of the possible solutions although the unique solution cannot be yielded.