8.4.2 Constant rate tests
Based on the result of a step drawdown test,we can select an appropriate pumping rate slightly smaller than the capacity of the well.Pump the water for a long period of time,and record the drawdown for each observation well.This section will introduce the analytical methods for constant rate pumping tests in confined and free aquifers,respectively.
1)Confined aquifers
Given the results of pumping tests of a confined aquifer,the coefficients of transmissivity and storage of the aquifer can be obtained by using the nonequilibrium and the equilibrium equations.Assuming the drawdown curve is under the nonequilibrium condition,according to Theis's nonequilibrium equation,we have
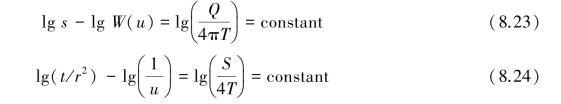
The relational curve of lg s-lg Q is called the standard curve,as shown in Figure 8.11.The relational curve of lg(t/r2)-lg(1/u)is called the data curve.From Eqs.8.23 and 8.24,we can see that the standard curve and the data curve are quite similar,given the same scale.If we superpose the two curves onto the same diagram of coordinates,the curves of lg s and lg W(u)are identical except for a shift of constant lg(Q/4πT).Similarly,the curves of lg(t/r2)and lg(1/u)are also identical except for a shift of constant lg(S/4T).Taking advantage of the characteristic between the standard curve and the data curve,the hydraulic parameters can be derived as follows:
①Depict the standard curve W(u)-(1/u)on the coordinate diagram on the logarithm scale.
②Depict the data curve s-t/r2 in the same scale as that of the standard curve on another coordinate diagram on the logarithm scale.If there exists only one observation well,the values of s and t obtained from the well can be directly adopted(i.e.r is a constant;t is a variable).If there is more than one observation well,we can also adopt the values of s-t/r2 at a specific time(i.e.t is a constant;r is a variable).
③Shift the coordinate sheets to make the data and standard curves meet.Be sure to keep the coordinates parallel to each other.
④Pick a point,called the matching point,and read the values of W(u),1/u,s and t/r2 at the point.
⑤Substitute the values of W(u),1/u,s and t/r2 into Eqs 8.1 and 8.3,obtain T and S
Since the computing of Theis's nonequilibrium equation is too complicated,it is rarely adopted,and Jacob's nonequilibrium equation is most widely used.When t is so great or r is small enough that u≤0.05,Jacob's nonequilibrium equation can be used to obtain hydraulic parameters.Similarly,we can depict the relations between s and lg t/r2,whose values are obtained from a certain observation well(i.e.r is a constant;t is a variable).If there is more than one well,the s-t/r2 relation at a specific time(i.e.t is a constant;r is a variable)can also be adopted.According to the s-lgt/r2 curve and Eq.8.5,we have

where
(Δs)J=slope of s-lg t/r2 curve,the value of which equals the decreased amount of s when
t/r2 increases by a factor of ten.
The coefficient of transmissivity can thus be derived using the above equation.If we extend the line segment of s-lg t/r2,corresponding value of t/r2 is(t/r2)s=0 where the extended line intersects with s=0 at(t/r2)s=0.According to Eq.8.5,we can compute the coefficient of storage by the following equation:

where
(t/r2)s=0 is the corresponding value of t/r2 when s=0.
If the drawdown curve of a pumping test reaches equilibrium or changes little,Thiem's equilibrium equation can then be adopted for the calculation of hydraulic parameters.According to Eq.8.8,the coefficient permeability can be obtained as follows:
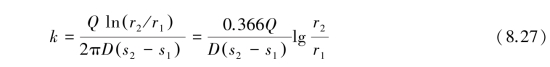
and the coefficient of transmissivity is

If there are two or more observation wells,first establish the relations between the drawdown(s)and the distance on the logarithm scale(log r)for each well.Then the coefficient of transmissivity can be derived from Eq.8.27 as

where
(Δs)T is the slope of slope of s-lgr curve and its value equals the decreased amount of s when r increases ten times.
Similarly,if we extend the line segment of the s-lg r curve,the extended line will intersect with s=0 at R.The same as earlier discussions,R represents the influence range of the drawdown.According to the influence range in Eq.8.6,the coefficient of storage can be derived as

The coefficient of transmissivity can also be derived from the recovery method.Similarly,depict the s′-lg(t/t′)relation according to the observation of each well.Using Eq.8.11,we can derive

where
(Δs′)r is the slope of slope of s′-lg(t/t′)curve and its value equals the decreased amount of s when r increases ten times.
2)Free aquifers
If the pumping⁃induced drawdown is much smaller than the thickness of the free aquifer,both Theis's nonequilibrium equation and Jacob's modified nonequilibrium equation for confined aquifers are applicable and the required hydraulic parameters are also the coefficients of transmissivity and storage.
If there are two observation wells,let the distances between the pumping well and the two observation wells be r1,and r2,respectively and the water levels in the two observation wells are separately h1 and h2.According to Eq.8.14,the coefficient of permeability will be

