7.5.1 Isotropic states of stress and strain(σ′1=σ′...
In the Soft Soil model,it is assumed that there is a logarithmic relation between changes in volumetric strain,εv,and changes in mean effective stress,p′,which can be formulated as
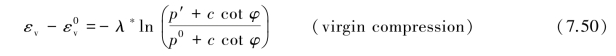
In order to maintain the validity of Eq.7.50,a minimum value of p′is set equal to a unit stress.The parameterλ∗is the modified compression index,which determines the compressibility of the material in primary loading.Note thatλ∗differs from the indexλas used by Burland(1965).The difference is that Eq.7.50 is a function of volumetric strain instead of void ratio.Plotting Eq.7.50 gives a straight line.
During isotropic unloading and reloading,a different path(line)is followed,which can be formulated as
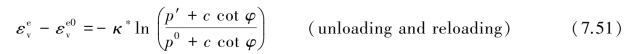
Again,a minimum value of p′is set equal to a unit stress.The parameterκ∗is the modified swelling index,which determines the compressibility of the material in unloading and subsequent reloading.Note thatκ∗differs from the index n as used by Burland.The ratioλ∗/κ∗is,however,equal to Burland's ratioλ∗/κ.The soil response during unloading and reloading is assumed to be elastic as denoted by the superscript e in Eq.7.51.The elastic behaviour is described by Hooke's law.Eq.7.51 implies linear stress dependency on the tangent bulk modulus as
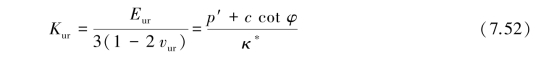
In which the subscript ur denotes unloading/reloading.Note that effective parameters are considered rather than undrained soil properties,as might be suggested by the subscripts ur.Neither the elastic bulk modulus,Kur,nor the elastic Young's modulus,Eur is used as an input parameter.Instead,vur andκ∗are used as input constants for the part of the model that computes the elastic strains.
An infinite number of unloading/reloading lines may exist in Figure 7.16,each corresponding to a particular value of the isotropic pre⁃consolidation stress pp.The pre⁃consolidation stress represents the largest stress level experienced by the soil.During unloading and reloading,this pre⁃consolidation stress remains constant.In primary loading,however,the pre⁃consolidation stress increases with the stress level causing irreversible(plastic)volumetric strains.
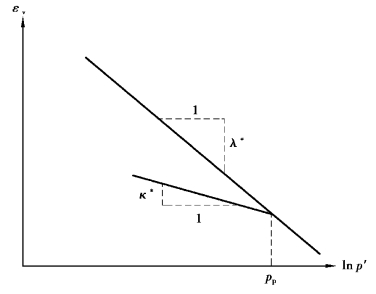
Figure 7.16 Logarithmic relation between volumetric strain and mean stress
