7.2.2 Basic parameters of the Mohr⁃Coulomb model
The linear elastic perfectly⁃plastic Mohr⁃Coulomb model requires a total of five parameters,which are generally familiar to most geotechnical engineers and which can be obtained from basic tests on soil samples.These parameters with their standard units are listed below:
E:Young's modulus [kN/m]
v:Poisson's ratio [—]
c:Cohesion [kN/m2]
φ:Friction angle [°]
ψ:Dilatancy angle [°]
σt:Tension cut⁃off and tensile strength[kN/m2]
Instead of using the Young's modulus as a stiffness parameter,alternative stiffness parameters can be entered.These parameters with their standard units are listed below:
G:Shear modulus [°]
Eoed:Oedometer modulus [kN/m2]
Parameters can either be effective parameters[indicated by a prime sign(′)]or undrained parameters(indicated by a subscript u),depending on the selected drainage type.
In the case of dynamic applications,alternative and/or additional parameters may be used to define stiffness based on wave velocities.These parameters are listed below:
Vp:Compression wave velocity [m/s]
Vs:Shear wave velocity [m/s]
(1)Young's modulus(E)
A stiffness modulus has the dimension of stress.The values of the stiffness parameter adopted in a calculation require special attention as many geomaterials show a non⁃linear behavior from the very beginning of loading.In triaxial testing of soil samples,the initial slope of the stress⁃strain curve(tangent modulus)is usually indicated as E0 and the secant modulus at 50% strength is denoted as E50(see Figure 7.2).For materials with a large linear elastic range,it is realistic to use E0;but for loading of soils,one generally uses E50.Considering unloading problems,as in the case of tunneling and excavations,one needs an unload⁃reload modulus(Eur)instead of E50.
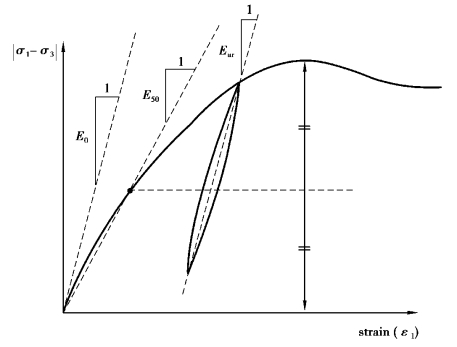
Figure 7.2 Definition of E0,E50,Eur for drained triaxial test results
For soils,both the unloading modulus,Eur and the first loading modulus,E50 tend to increase with the confining pressure.Hence,deep soil layers tend to have greater stiffness than shallow layers.Moreover,the observed stiffness depends on the stress path that is followed.The stiffness is much higher for unloading and reloading than for primary loading.Also,the observed soil stiffness in terms of a Young's modulus may be lower for(drained)compression than for shearing.Hence,when using a constant stiffness modulus to represent soil behavior,one should choose a value that is consistent with the stress level and the stress path development.
In real soils,the stiffness depends significantly on the stress level,which means that the stiffness generally increases with depth.When using the Mohr⁃Coulomb model,the stiffness is a constant value.In order to account for the increase of the stiffness with depth,the Einc⁃value may be used,which is the increase of the Young's modulus per unit of depth(expressed in the unit of stress per unit depth).At the level given by the ref parameter,and above,the stiffness is equal to the reference Young's modulus,Eref,as entered in the Parameters tabsheet.Below,the stiffness is given by
![]()
where y represents the vertical direction.The actual value of Young's modulus in the stress points is obtained from the reference value and Einc.Note that during calculations,a stiffness increasing with depth does not change as a function of the stress state.
(2)Poisson's ratio v
Standard drained triaxial tests may yield a significant rate of volume decrease at the very beginning of axial loading and,consequently,a low initial value of Poisson's ratio(v0).For some cases,such as particular unloading problems,it may be realistic to use such a low initial value,but in general,when using the Mohr⁃Coulomb model,the use of a higher value is recommended.
The selection of a Poisson's ratio is particularly simple when the elastic model or Mohr⁃Coulomb model is used for gravity loading under conditions of one⁃dimensional compression.For this type of loading,PLAXIS give realistic ratios of K0=σ′h/σ′v.As both models will give the well⁃known ratio ofσ′h/σ′v=v/1-v for one⁃dimensional compression,it is easy to select a Poisson's ratio that gives a realistic value of K0.Hence v is evaluated by matching K0.In many cases one will obtain v values in the range between 0.3 and 0.4.In general,such values can also be used for loading conditions other than one⁃dimensional compression.Please note that in this way it is not possible to create K0 values larger than 1,as may be observed in highly overconsolidated stress states.For unloading conditions,however,it is more appropriate to use values in the range between 0.15 and 0.25.
(3)Cohesion(c)or undrained shear strength(su)
The cohesive strength has the dimension of stress.In the Mohr⁃Coulomb model,the cohesion parameter may be used to model the effective cohesion c of the soil(cohesion intercept),in combination with a realistic effective friction angleφ′[see Figure 7.3(a)].This may not only be done for drained soil behavior,but also if the type of material behavior is set to Undrained(A).
Alternatively,the cohesion parameter may be used to model the undrained shear strength su of the soil,in combination with p=u=0 when the Drainage type is set to Undrained(B)or Undrained(C).In that case the Mohr⁃Coulomb failure criterion reduces to the well⁃known Tresca criterion.
The disadvantage of using effective strength parameters c′andφ′in combination with the drainage type being set to Undrained(A)is that the undrained shear strength as obtained from the model may deviate from the undrained shear strength in reality because of differences in the actual stress path being followed.In this respect,advanced soil models generally perform better than the Mohr⁃Coulomb model,but in all cases it is recommended to compare the resulting stress state in all calculation phases with the present shear strength in reality(![]() ).
).
On the other hand,the advantage of using effective strength parameters is that the change in shear strength with consolidation is obtained automatically,although it is still recommended to check the resulting stress state after consolidation.The advantage of using the cohesion parameter to model undrained shear strength in combination with y=0(Undrained(B)or Undrained(C))is that the user has direct control over the shear strength,independent of the actual stress state and stress path followed.Please note that this option may not be appropriate when using advanced soil models.
(4)Friction angle(φ)
The friction angleφis entered in degrees.In general,the friction angle is used to model the effective friction of the soil,in combination with an effective cohesion c[Figure 7.3(a)].This may not only be done for drained soil behavior,but also if the type of material behavior is set to Undrained(A).Alternatively,the soil strength is modelled by setting the cohesion parameter equal to the undrained shear strength of the soil,in combination withφ=0(Undrained(B)or Undrained(C))[Figure 7.3(b)].In that case the Mohr⁃Coulomb failure criterion reduces to the well⁃known Tresca criterion.
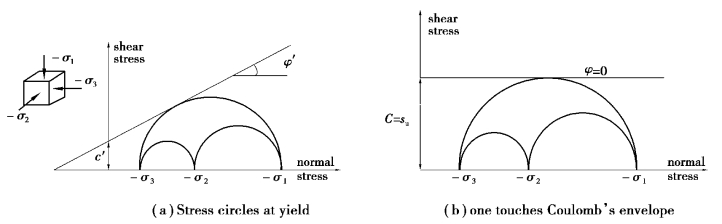
Figure 7.3 Failure criterion and the friction angle
High friction angles,as sometimes obtained for dense sands,will substantially increase plastic computational effort.Moreover,high friction may be subjected to strain⁃softening behavior,which means that such high friction angles are not sustainable under(large)deformation.Hence,high friction angles should be avoided when performing preliminary computations for a particular“project”.The friction angle largely determines the shear strength as shown in Figure 7.3 by means of Mohrs stress circles.A more general representation of the yield criterion is shown in Figure 7.4.The Mohr⁃Coulomb failure criterion proves to be better for describing soil strength for general stress states than the Drucker⁃prager approximation.Typical effective friction angles are in the order of 20⁃30 degrees for clay and silt(the more plastic the clay,the lower the friction),and 30⁃40 degrees for sand and gravel(the denser the sand,the higher the friction).
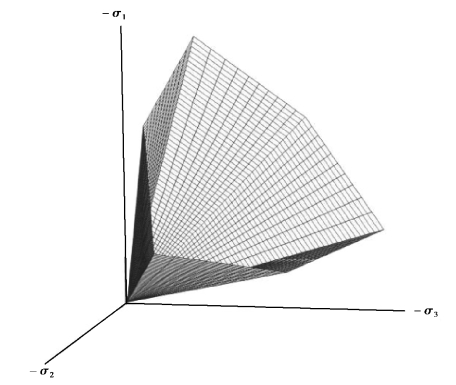
Figure 7.4 Failure surface in principal stress space for cohesionless soil
(5)Dilatancy angle(ψ)
The dilatancy angle,ψ(psi),is specified in degrees.Apart from heavily over⁃consolidated layers,clay soils tend to show little dilatancy(ψ≈0).The dilatancy of sand depends on both the density and the friction angle.In general,the dilatancy angle of soils is much smaller than the friction angle.For quartz sands the order of magnitude isψ≈φ-30°.Forφvalues of less than 30,however,the angle of dilatancy is mostly zero.A small negative value for is only realistic for extremely loose sands.In the Hardening Soil model or Hardening Soil model with small⁃strain stiffness,the end of dilatancy,as generally observed when the soil reaches the critical state,can be modelled using the Dilatancy cut⁃off.However,this option is not available for the Mohr⁃Coulomb model.For further information about the link between the friction angle and dilatancy,see Bolton(1986).
A positive dilatancy angle implies that in drained conditions the soil will continue to dilate as long as shear deformation occurs.This is clearly unrealistic,as most soils will reach a critical state at some point and further shear deformation will occur without volume changes.In undrained conditions,a positive dilatancy angle,combined with the restriction on volume changes,leads to a generation of tensile pore stresses.In an undrained effective stress analysis,therefore,the strength of the soil may be overestimated.When the soil strength is modelled as undrained shear strength,su,andφ=0,(Undrained(B)or Undrained(C))the dilatancy angle is automatially set to zero.Great care must be taken when using a positive value of dilatancy in combination with drainage type set to Undrained(A).In that case the model will show unlimited soil strength due to tensile pore stresses.These tensile pore stresses can be limited by setting the cavitation cut⁃off.
(6)Shear modulus(G)
The shear modulus,G,has the dimension of stress.According to Hooke's law,the relationship between Young's modulus E and the shear modulus is given by(see Eq.7.17)

Entering a particular value for one of the alternatives G or Eoed results in a change of the E modulus whilst v remains the same.
(7)Oedometer modulus(Eoed)
The oedometer modulus,Eoed,or constrained modulus has the dimension of stress.According to Hooke's law,the relationship between Young's modulus E and the oedometer modulus is given by(see Eq.7.18)

Entering a particular value for one of the alternatives G or Eoed results in a change of the E modulus whilst v remains the same.
