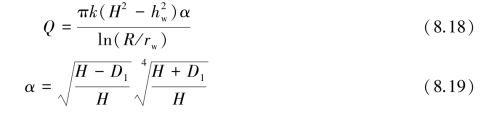8.3.2 Free aquifers
A free aquifer,also called an unconfined aquifer,refers to an aquifer which is exposed to the atmosphere and is underlain by an impermeable layer.The analyses of free aquifers are also divided into full penetration wells and partial penetration wells.
1)Full penetration well
The solution for nonequilibrium equations of pumping⁃induced draw down in free aquifers is quite complicated.The reason is mainly that the coefficient of transmissivity is not a constant and varies with pumping time and distance.In addition,the vertical directions of flow near the well are so crucial that they cannot be ignored in the derivation.
On the other hand,if the drawdown is much smaller than the thickness of aquifers,the thickness of aquifers can thus be assumed to be a constant during dewatering.Since the coefficient of transmissivity is the product of the coefficient of permeability and the thickness of the aquifer,the coefficient of transmissivity is also a constant.Theis's nonequilibrium equation or Jacob's modified nonequilibrium equation can also be applied to pumping in free aquifers accordingly.The required hydraulic parameters are also the coefficients of transmissivity(T)and storage(S).
As in Section 8.3.1,the coefficient of storage is given as the drained volume of the pore water due to lowering a unit head per unit surface area of an aquifer.The drainage per unit surface area of a free aquifer is caused by the decline of groundwater level.Therefore,in a free aquifer,the coefficient of storage is the same as the ratio of free water in the soil to the soil volume(Powers,1992).Its value is either smaller than or the same as the porosity of soil.For example,if the porosity of soil is 30% and two⁃thirds of pore water is drained as a result of the lowering of groundwater level by pumping,the coefficient of storage will then be 20% or 0.2.For most free aquifers,the coefficient of storage would be around 0.2⁃0.3.
As shown in Figure 8.13,under the Dupuit⁃Thiem assumption(Thiem,1906),the equilibrium equation of drawdown of a full penetration well in a free aquifer is

Where h1 and h2 are the heights of the water levels at the distances of r1 and r2,respectively.Substitute the influence range(R)and the radius of the well(rw)for r2 and r1,respectively,in the above equation,then we have
Figure.8.13 Drawdown in free aquifers for the full penetration well

Rewrite equation to obtain the groundwater level or drawdown at any distance(r)as follows:

or

where
h is the groundwater level at the distance of r.
2)Partial penetration well
The same as the full penetration well,the nonequilibrium equation of drawdown of a partial penetration well is rather complicated and is not to be discussed here.This section only introduces
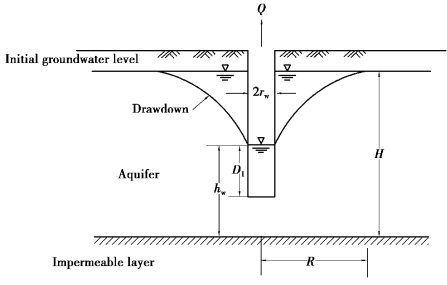
Figure 8.14 Drawdown in free aquifers for the partial penetration well
an equation proposed by Hausman(1990),which is