3.6.4 变形计算时间与角色个数的关系
本章提出的基于自适应网格的图像变形算法,是针对多角色的同时变形设计的,由于自适应网格的影响因素局部化和图形硬件加速,使得该算法的执行速度很快。
下面的实验以Frog角色图像为例,网格精细程度设定为每个自适应网格包含40个三角形,每次实验连续记录100帧取平均值,统计各步骤运行时间与角色个数的关系。
(1)统计角色个数不同所引起的初始化各步骤时间变化。各步骤运行时间见表3-7。由表中可以看出,在角色变形过程中,由于对所有角色使用的是同一个图像,图像加载和纹理坐标计算的时间与角色数量无关,基本保持不变。
表3-7 变形初始化各步骤时间 (单位:ms)
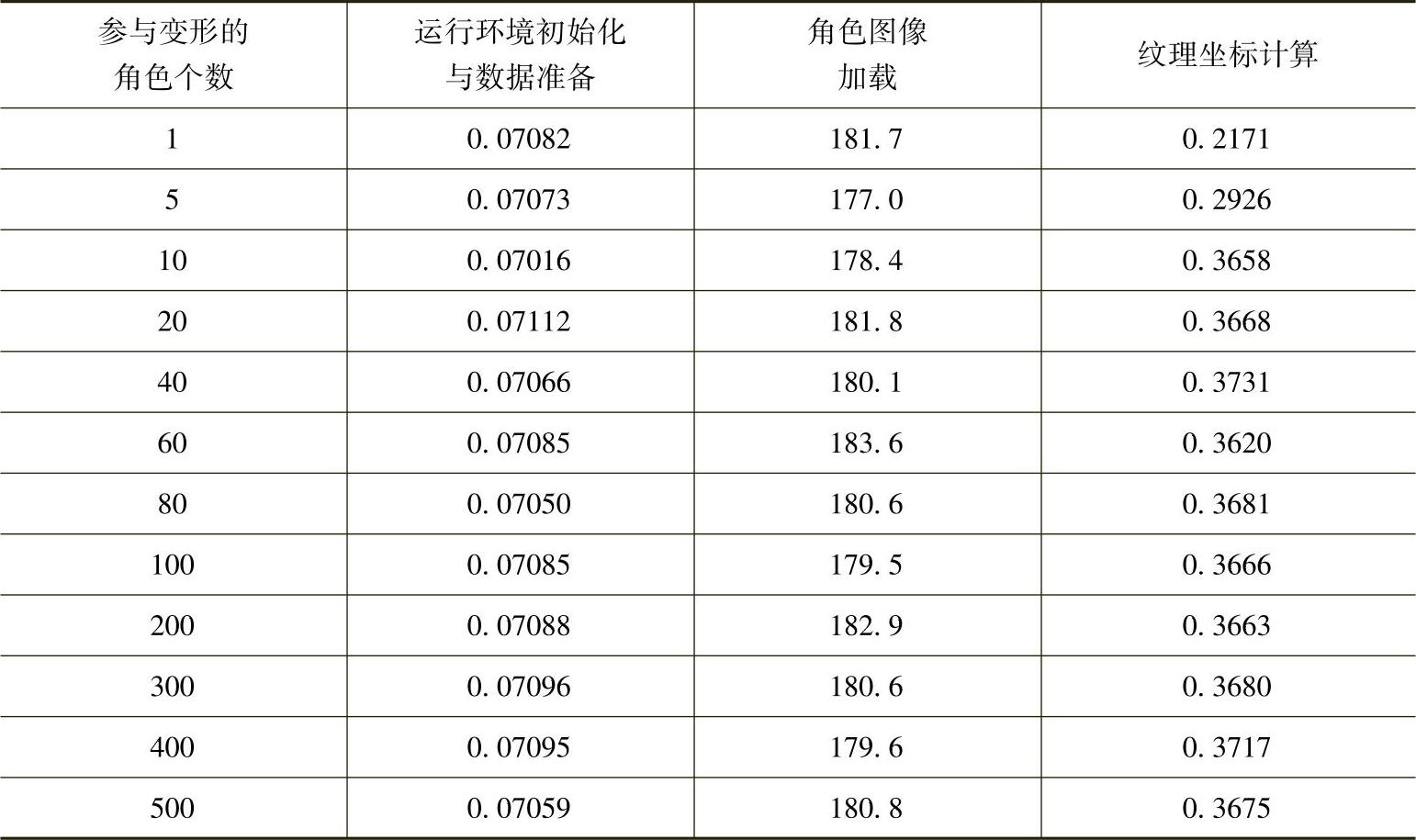
(2)统计角色个数不同引起的CPU、GPU二次渲染和GPU一次渲染等方法中运行时各步骤所需的时间变化。CPU方法各步骤所需的运行时间统计见表3-8。
表3-8 传统CPU方法所需的运行时间 (单位:ms)
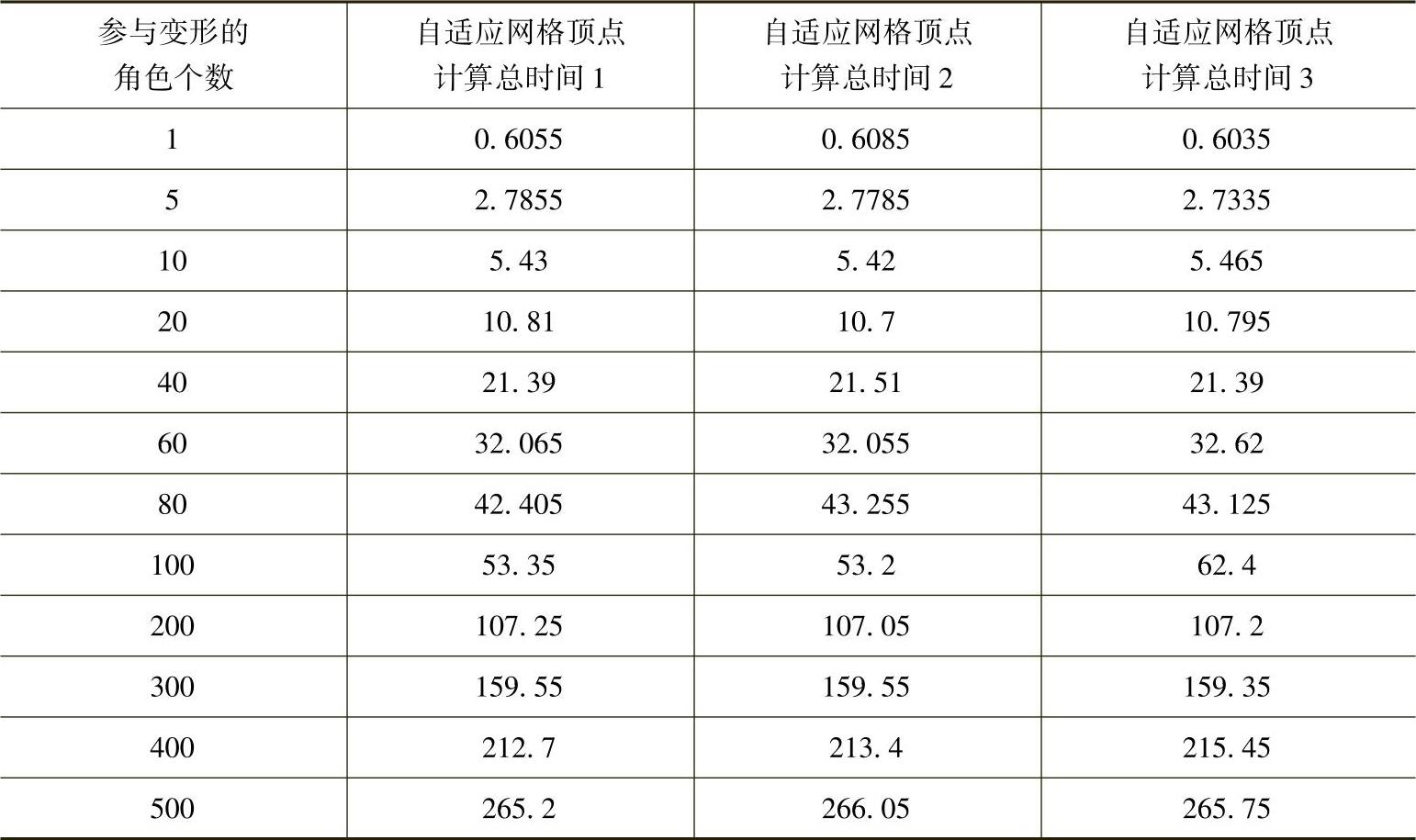
根据表3-8所示的数据,获得的传统CPU方法变形计算的运行时间与角色个数关系图如图3-24所示。
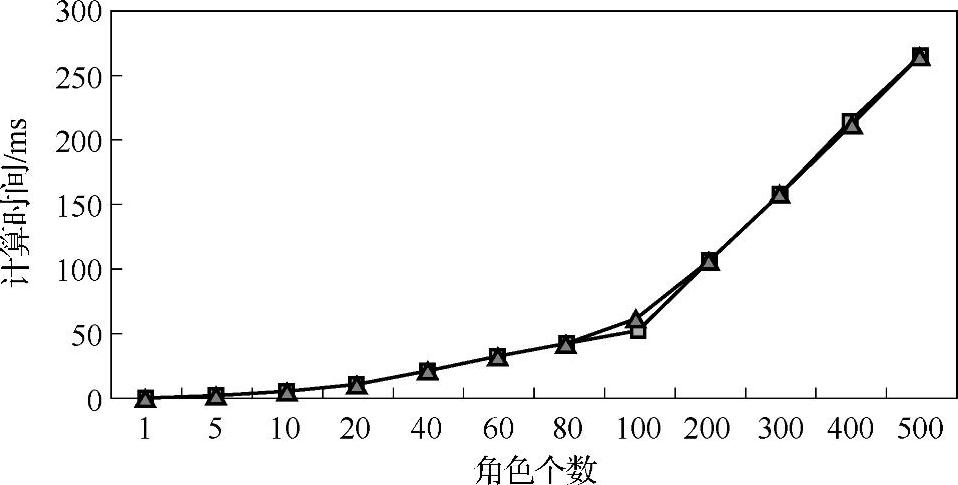
图3-24 CPU方法变形计算时间与角色个数关系图
(3)在GPU二次渲染方法的计算过程中,将角色网格顶点的计算结果暂时保存到显存的FBO纹理中,然后返回到内存进行二次渲染。FBO纹理的每一行,对应角色的每一个关节点,本实验中的每个角色有12个关节点,由于本实验中使用的显卡,所支持的纹理最大为4096行,因此最大只能支持4096/12=341个Frog角色的同时变形。不同角色个数的GPU二次渲染方法中各步骤的运行时间统计见表3-9。
表3-9 GPU二次渲染方法中各步骤的运行时间 (单位:ms)(https://www.daowen.com)
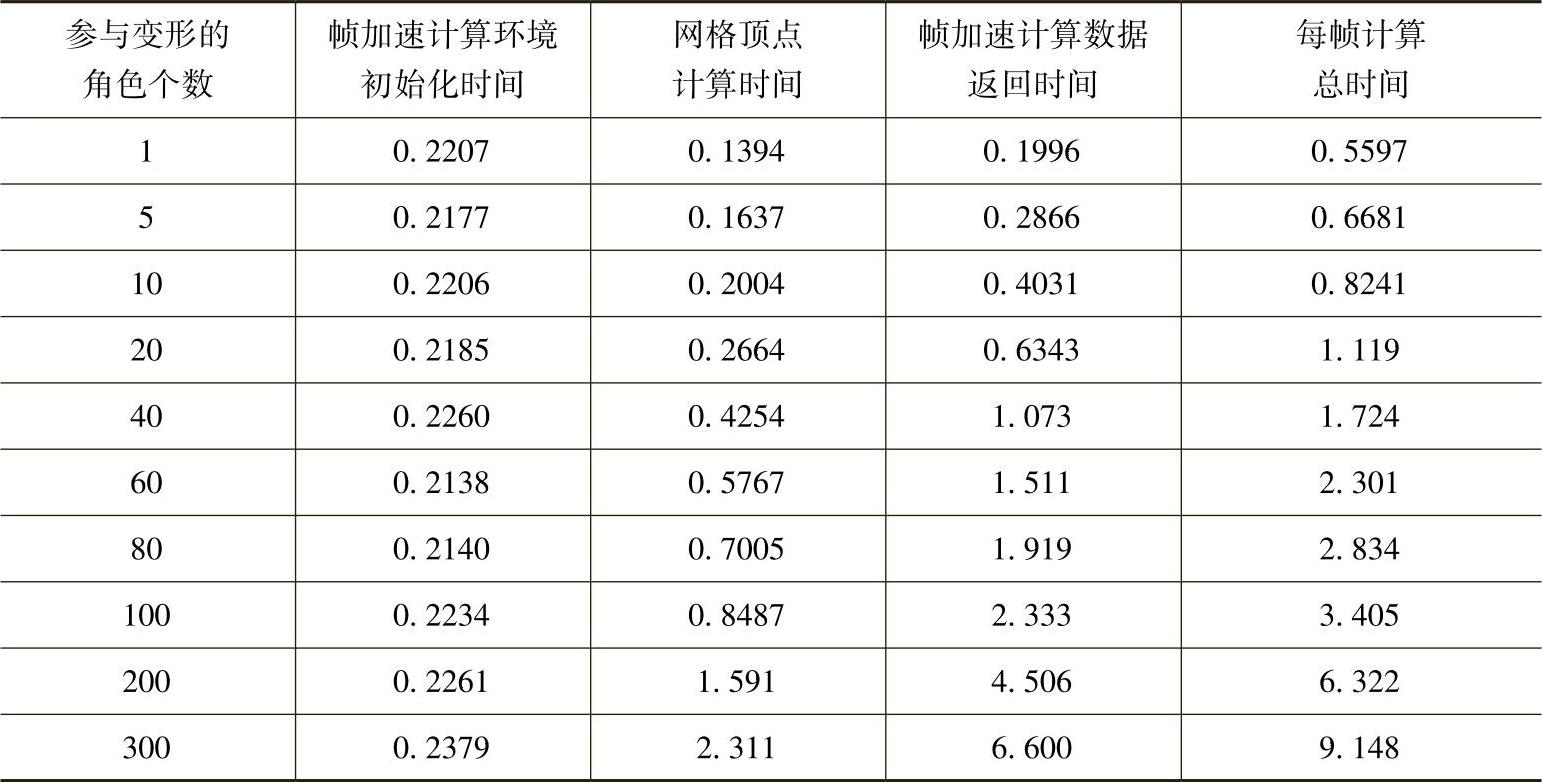
根据表3-9所获得的GPU二次渲染方法运行时间与角色个数关系如图3-25所示。在所支持的变形实验结果中可以看出,随着角色数量的增多,计算环境初始化时间基本保持不变,顶点计算时间逐渐增大,而数据返回时间与数据量基本成正比。
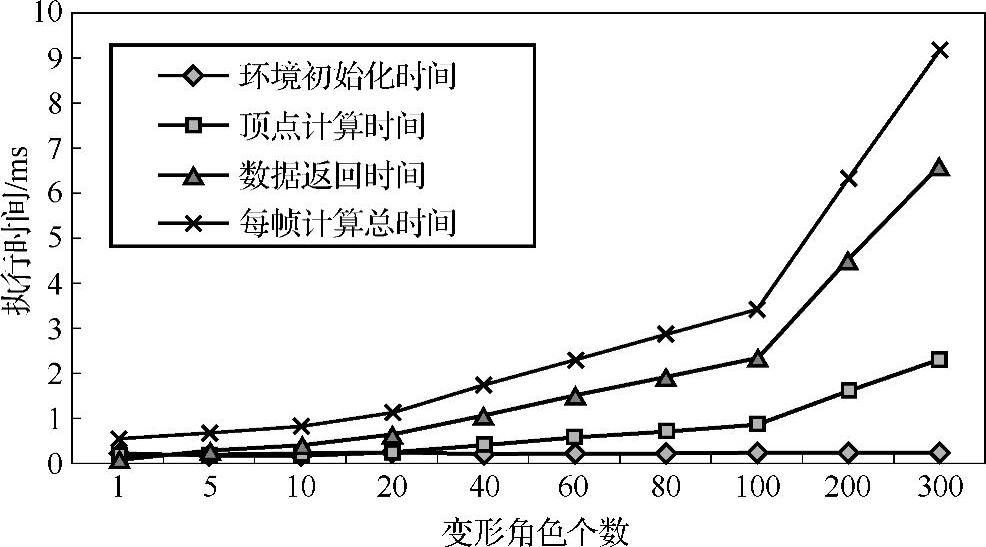
图3-25 GPU二次渲染方法运行时间与角色个数关系图
(4)GPU一次渲染方法中各步骤的运行时间统计见表3-10。
表3-10 GPU一次渲染方法所需的运行时间 (单位:ms)
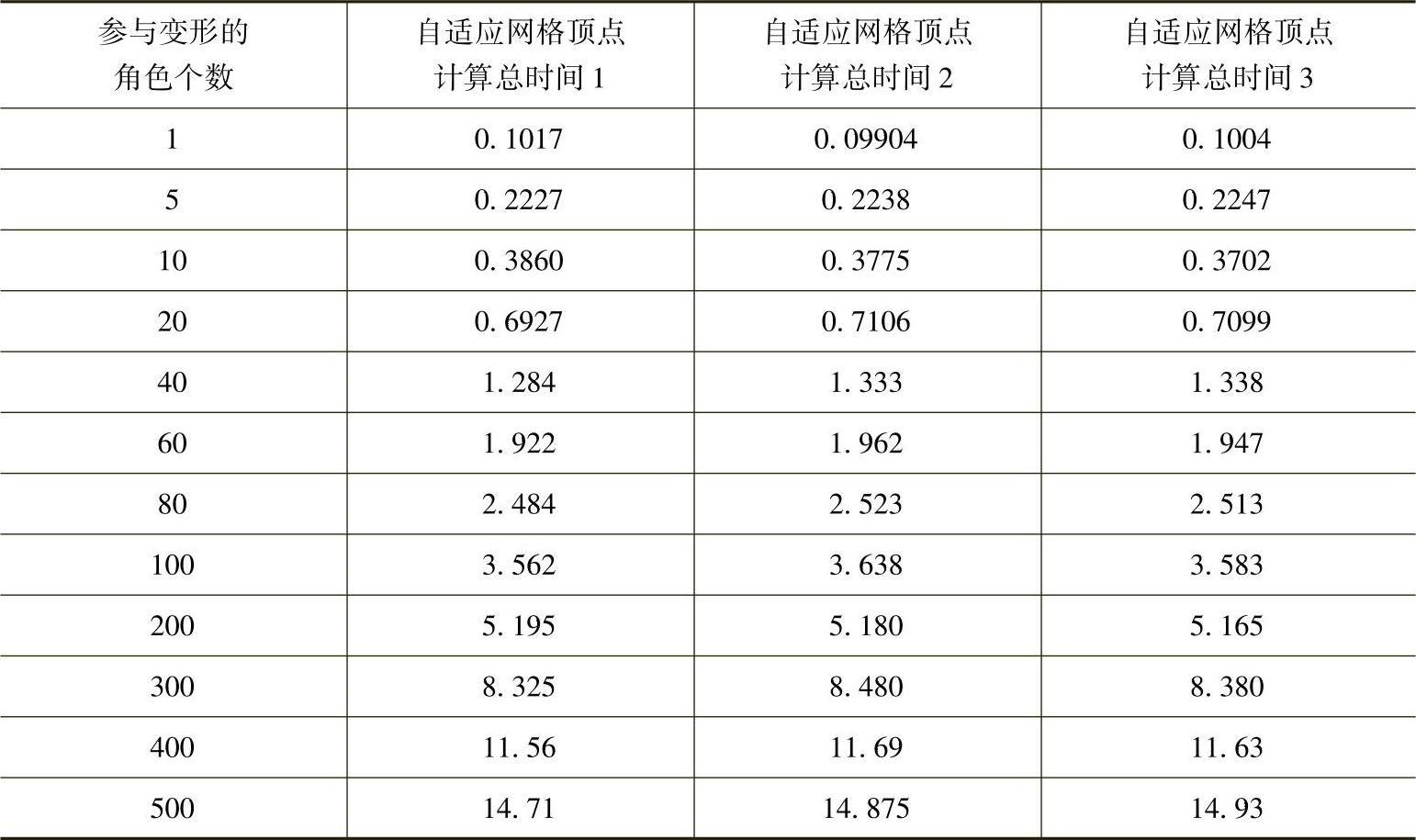
根据表3-10所得到的GPU一次渲染方法变形计算时间与变形角色个数的关系如图3-26所示。由图中可以看出,GPU一次渲染方法的变形计算时间与变形角色个数基本成正比,这是由于该方法不需要每帧计算的初始化,与CPU一样只需要计算过程。
(5)根据上述实验中对CPU、GPU二次渲染和GPU一次渲染的变形计算的时间统计,可得三种计算方法随角色数量变化的执行时间对比如图3-27所示。
通过本节的实验可以看出,GPU对于关节点数目较多的情况中有明显的计算优势,而GPU一次渲染方法比GPU二次渲染方法的适用范围更广,GPU二次渲染方法适合于大量顶点的计算,而GPU一次渲染加速方法适合于小计算量的硬件加速实现。对于GPU二次渲染加速方法,随着变形角色的个数少于5个时,CPU的计算速度更快,当关节点个数超过5个时,GPU的计算速度将很快超过CPU,计算时间大大缩短,这是由于渲染目标的设置时间造成的,当渲染目标的切换时间大于CPU/GPU的计算差距,则GPU的每帧计算时间长,反之则CPU计算时间长。而对于GPU一次渲染加速方法,则计算速度始终快于CPU。
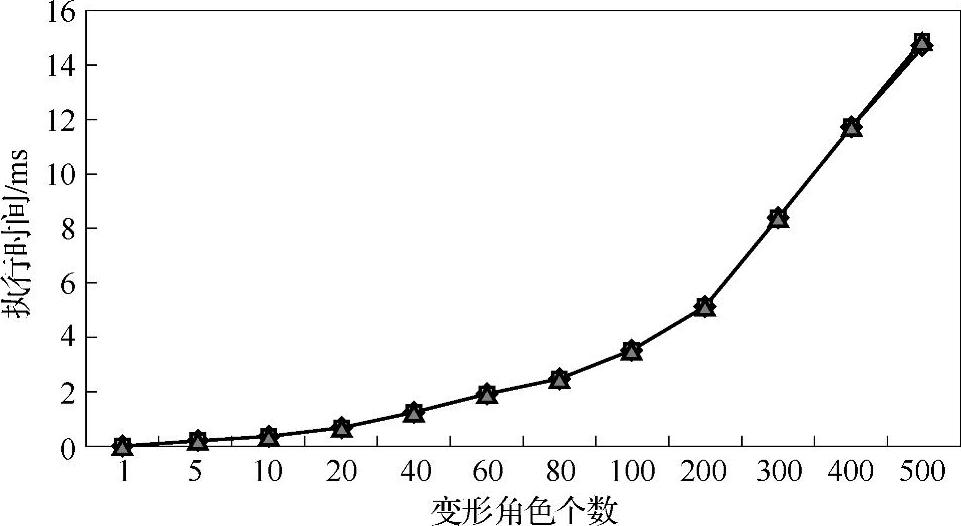
图3-26 GPU一次渲染方法运行时间与角色个数关系图
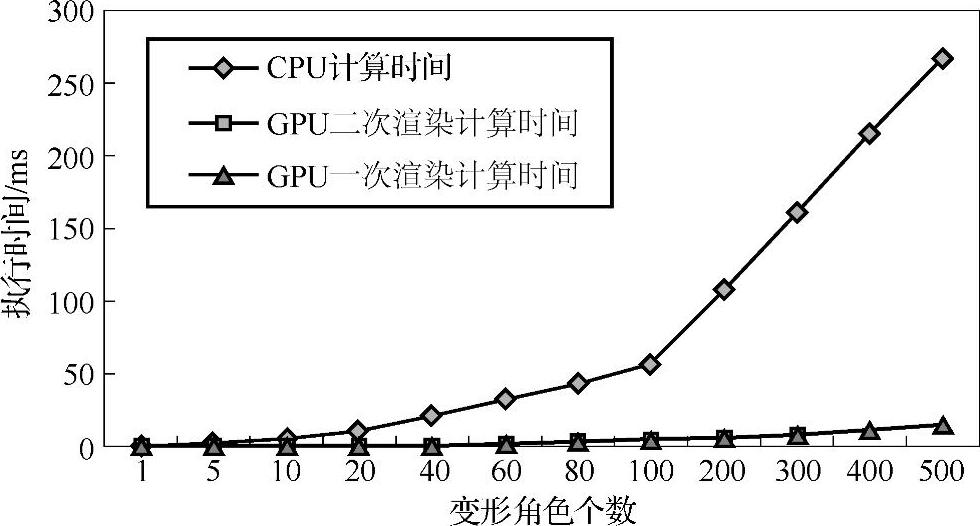
图3-27 不同角色个数的三种方法计算时间比较
