4.1.2　正弦量的相量表示法

4.1.2　正弦量的相量表示法

正弦量的相量表示法

在线性电路中，如果激励是正弦量，则电路中各支路的电压、电流的稳态响应将是同频率的正弦量。同时，若电路中有多个激励均为同频率的正弦量，则根据线性电路的叠加定理，电路全部稳态响应也是同一频率的正弦量。

一个正弦量具有幅值、频率和初相位三个要素。在分析计算线性电路时，电路中各部分电压和电流都是与电源同频率的正弦量，因此，频率是已知的，计算时可不必考虑。这样，一个正弦量就可与一个复数一一对应。复数的模对应正弦量的幅值（或有效值），辐角对应正弦量的初相角。表示正弦量的复数称为相量。

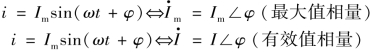
例如：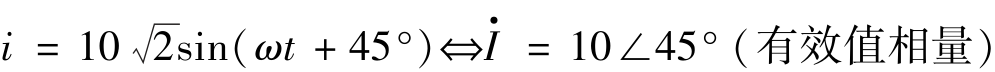

　　　

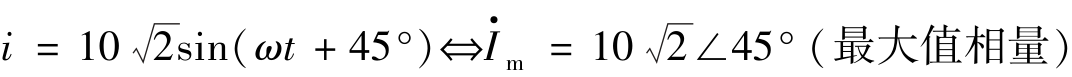
相量和复数一样，也可以在复平面上用矢量来表示，表示相量的图称为相量图。

需要强调的是：

（1）正弦量的相量和它时域内对应的函数表达式是一一对应的关系，不是相等的关系。

（2）只有正弦量才能用相量表示，非正弦量不可以。

（3）若已知正弦量的瞬时值表达式，可直接写出与之对应的相量，反之，若已知正弦量的相量，须再知道其角频率才能写出与之对应的函数表达式。

（4）在实际应用中，更多采用有效值相量。

（5）只有同频率的正弦量才能画在一张相量图上，不同频率不可以。

（6）相量有两种表示方法：相量表达式和相量图。