第十七章 论理性
§1.斐 在各别地谈到信仰之前,我们将先来讨论理性[1]。这个词有时意指明白和真正的原则,有时指从这些原则演绎出来的结论,而有时则指原因,特别是指目的因。这里我们是把它看作一种功能,由于它我们把人看作有别于禽兽,并且在这方面人显然是大大超过禽兽的。§2.我们之需要理性,既为了扩大我们的知识,也为了规范我们的意见,而正确理解起来,它构成两种功能,这就是用来找出中介观念的机敏(sagacité),和得出结论或推论(inférer)的功能。§3.而我们可以考虑在理性中有这四个等级:(1)发现证据;(2)把它们安排成秩序,使人看出其联系;(3)察觉演绎的每一部分中的联系;(4)从之得出结论。而我们在数学的推证中就可以看到这四个等级。
德 理性[2]是被认识了的真理,它和另一较少被认识的真理的联系,使我们给后者以同意。但它如果不仅是我们的判断的原因,而且还是真理本身的原因时,我们更特别和突出地称之为理性,这就是我们也称之为先天理性(raison a priori)的,而事物方面的原因,就相应于真理方面的理性。这就是为什么原因本身,特别是目的因,之所以常常被称为理性的缘故。最后是那察觉这种真理的联系的功能,或推理的功能,也被称为理性,而这就是您在这里所用的意义。而这种功能在我们这尘世间是只有人才真正具有的,尘世间的其他动物并没有表现出有这种功能;因为我在上面已经指出过,在禽兽中所看到的那种理性的影子,只是在一种显得和过去相似的情况下期待出现相似的事,而并不知道是否有同样的理性在起作用。人们本身在他们仅仅是凭经验的(empiriques)情况下,行事的方式也并不两样。但他们只要看到了真理之间的那些联系,就超出了禽兽之上;这些联系,我说,本身也构成了必然和普遍的真理。这些联系,即使只产生一种意见,当经过切实研究之后,就我们所能判断范围内的概然性的优势地位可以得到证明时,其实也是必然的,以致那时就也有一种推证,这不是关于事物的真实性的推证,而是关于审慎的思虑要求我们采取哪一边的立场的推证。在划分这种理性的功能时,我认为我们依照一种相当为人们所接受的意见,即把发明和判断加以区别,而承认它有两部分,这样做是不错的。至于您所指出的在数学的推证中的四个等级,我发现那第一个,即发现证据,通常是并不如所希望那样在其中出现的。有一些综合,有时被发现是没有分析的,有时分析是被免除了的。几何学家们在作他们的推证时,首先提出要证明的命题,而为了来作证明他们就作出某种被给定的图形。这就是所谓的列题(Ecthèse)。这以后,他们就来作准备,并画一些为他们作推理所需要的新的线;而往往最大的技巧就在于找出这种准备。这样做了之后,他们就来进行推理本身,从那在列题中已给定的和在准备中所加的作出推论;而为此目的运用着已知或已证明的真理,他们就达到了结论。但有些场合他们也不用列题和准备。
§4.斐 人们一般地认为三段论是理性的重大工具和运用这种功能的最好手段。就我来说,我怀疑这一点,因为它只有助于在单独一个例子中看出证据间的联系而再没有别的;但心灵没有它也一样容易地能看得出甚至也许能更好地看出这种联系。那些知道怎样运用三段论的格和式的人,往往只是凭对他们老师的一种盲目信仰把这种用法视为当然而并不知其所以然的理由。要是三段论是必要的,那么在它被发明以前就没有什么人凭理性知道任何东西了,并且得说上帝把人造成为两条腿的生物之后,就留给亚里士多德来使他成为一个理性的动物;我所指的就是只有为他所能引使来考察三段论的基础的这少数人,这方面,在形成那三个命题〈的三段论〉的60种方式中,只有约14种是可靠的。但上帝对人们却有更多得多的善意;他给了他们一个能作推理的心灵。我这里所说的并不是要来贬低亚里士多德,我把他看作是古代最伟大的人物之一,在广博、精细、心灵的深入透辟以及判断的有力等方面都很少有人能和他相比,并且就是他发明了论证形式的这短小体系这件事本身,也大大有助于学者们来反对那些毫不羞耻地否定一切的人。可是这些形式却并不是推理的唯一和最好的手段;并且亚里士多德也并不是利用这些形式本身来找到它们的,而是通过观念的明显符合这一原始途径找到的;而我们凭借数学证明中的自然秩序所得到的关于它们的知识,不求助于任何三段论还表现得更好。推论就是假定着一些中介观念的一种一定的联系,而从一个已提出作为真的命题,引出另一个作为真的命题;例如,从人们在来世将受惩罚,推论出他们在这里是能自作决定的。其联系如下:人们将受惩罚而上帝是施行惩罚者;因此这惩罚是公正的;因此那受惩罚者是有罪的;因此他本来是能够以别的方式行事的;因此他是有自由的;最后因此他是有自行决定的能力的。这联系在这里比之用五六个错综复杂的三段论看得还更清楚,在用那么些三段论的情况下,这些观念将被移位、重复和嵌进一些人为的形式中去。问题是要知道在三段论中一个中介观念和两端观念有什么样的联系,而这正是没有任何三段论能加以显示的。是心灵才能察觉这些观念,这样用一种并列的方式安排起来,而这是用它自己的眼光来察觉的。那么三段论有什么用呢?它在经院中有用,在那里人们毫无羞耻地否认显然可见地相符合的观念之间的符合。因此人们在寻求真理或教导那些真诚求知的人们时是绝不搞三段论的。也很显然,这样一种秩序:
人——动物——生物
也就是:人是一种动物,而动物是生物,因此人是生物,比之于三段论的这种秩序:
动物——生物。人——动物。人——生物。
也就是:动物是生物,人是一种动物,因此人是生物,是更为自然的。诚然,三段论可以有助于来发现借助于修辞学的华丽辞藻掩盖下的虚妄性,而我从前也曾认为三段论是必要的,至少对于防范那种花言巧语掩盖下的诡辩是必要的;但在更严格的考察之后,我发现只要把那些结论所依据的观念,和那些多余的观念分开,并把它们安排成一种自然的秩序,以显示出其前后不一贯就可以了。我曾认识一个人,完全不知道三段论的那些规则,却能立即觉察出一篇很长的巧伪而貌似有理的言辞中的弱点和虚妄处,而另外一些受过逻辑的全部精巧技术训练的人却让它骗过了;我相信在我的读者之中很少有人会不认识这样的人的。如果不是这样,那么那些君主们在有关他们的王位和他们的尊严的事情上,就不会不在最重要问题的讨论中运用三段论,可是人人都认为这样用是一件可笑的事情。在亚洲,在非洲,在美洲,在那些独立不依于欧洲人的民族中,任何人都几乎从来没有听说过三段论。最后,归根到底算起来,这些经院的形式也并不会少犯些错误;人们也罕见被这种经院的办法弄得哑口无言,更罕见为它所说服和战胜的。他们顶多承认他们的对手比自己更精巧,但他们还是仍然深信自己的道理是正当的。而如果人们能够在三段论中包含谬误推理,那么这种谬误就能用三段论之外的其他方法来加以发现。可是我并不是主张人们抛弃三段论,也不是要人们被剥夺了能有助于理智的任何手段。有些眼睛是需要戴眼镜的;但那些戴眼镜的人不应该说没有眼镜就什么人也看不清楚。这样就会过于贬低自然来抬高一种技术了,他们也许是受惠于这种技术的。除非是他们碰到和这样一些人所经验的完全相反的情况,这些人眼镜用得过多或过早了,视觉就因此被弄得如此模糊,以致不求助于眼镜就再也不能看东西了。
德 您关于三段论无用这一点的推理是充满着大量坚实而美好的意见的。也应该承认三段论的经院的形式世上是很少用的,并且如果认真地要那样用起来也太冗长,太麻烦了。可是,您相信吗?我主张,三段论形式的发明是人类心灵最美好,甚至也是最值得重视的东西之一。这是一种普遍的数学,它的重要性还没有被充分认识;并且我们可以说,其中包含着一种不谬性的技术(un art d'infaillibilité),只要是我们知道并且能够很好地加以运用的话,这不是永远能办得到的。然而要知道,所谓形式的论证(les argumens en forme),我理解为不仅是指在学院中所用的那种经院式的论证方式,而是指凭形式的力量得出结论,并且不需要补充任何项目的一切推理;所以一种堆垛(sorites),即另一种避免了重复的三段论的链,甚至一篇开列得很好的账目,一种代数的演算,一种无穷小的分析,在我看来都差不多是形式的论证,因为它们的推理的形式都是已预先经过推证了的,以致我们靠得住不会受骗弄错。而欧几里得的那些证明也往往就差不多是形式的论证;因为当他看起来在作省略三段论推理时,那被省略和似乎缺了的命题,是用注在边上的引证作了补充的,那里就让人有办法找到那命题是已经证明了的;这就大大地缩短了而又丝毫不减弱力量。他所用的这些戾换(inversions)、组合和理由的划分,只是一些适合于数学家和他们所处理的题材的特殊种类的论证形式,而他们借助于逻辑的普遍形式证明了这些特殊形式。还有,要知道有一些正确的非三段论的结论,也不能严格地用任何三段论来证明而不稍稍改变其名词的;而这些名词的改变本身就使结论成为非三段论的。这样的推论有好多种,如在别的之外就有a recto ad obliquum[3];例如:耶稣基督是上帝;因此耶稣基督的母亲是上帝的母亲。还有那高明的逻辑学家们称为关系的戾换的,例如这个推论:如果大卫是所罗门的父亲,则无疑所罗门是大卫的儿子。而这些结论也仍然可以用通常的三段论本身所依据的那些真理来加以证明的。三段论也并不仅仅是直言的,而是还有假言的,其中也包括选言的。我们可以说直言三段论有简单的和复杂的。简单的直言三段论就是人们通常算的那些,也就是按照各个格中的各个式的那些;而我发现四个格每个各有六个式,所以一共有24个式。第一格中通常的四个式,无非是所有、没有、有些这三个记号所指意义的结果。而我为了毫不省略起见加上的两个,无非是从属于全称命题之下的特称命题。因为从这通常的两个式,即:所有B是C,所有A是B,因此所有A是C;还有:没有B是C,所有A是B,因此没有A是C,我们可以作出这两个外加的式,即:所有B是C,所有A是B,因此有些A是C;还有:没有B是C,所有A是B,因此有些A不是C。因为没有必要来推证那特称命题和证明它的结论:所有A是C,因此有些A是C;以及没有A是C,因此有些A不是C,虽然我们也可以用同一性命题结合第一格中已被接受的式来加以证明如下:所有A是C,有些A是A,因此有些A是C;还有:没有A是C,有些A是A,因此有些A不是C。这样一来,第一格外加的两个式,用这一格通常的头两个式,插进特称命题就得到证明了,这特称命题本身又可以用同一个格的其余两个式来加以证明。用同样的方式,第二格也可以加上两个新的式。这样,第一格和第二格各有六个式;第三格是历来就都有六个式的;人们给了第四格五个式,但我们发现它据同样的增加的原则也有六个式。但必须知道逻辑的形式并不强迫我们采取通常所用的这种命题的次序,而我同意您的意见,先生,下列这另一种安排是更好的,即:所有A是B,所有B是C,因此所有A是C,这在用那种堆垛时就特别会是这样,这种堆垛就是这样的三段论的一条链。因为要是还有这样一个三段论:所有A是C,所有C是D,因此所有A是D,我们可以把这两个三段论作成一条链,而避免了重复,说:所有A是B,所有B是C,所有C是D,因此所有A是D,这里我们看到,所有A是C这个无用的命题被省略了,而两个三段论所要求的这同一个命题的无用的重复被避免了;因为这个命题以后就无用了,而这条链,当其力量靠用这两个三段论一劳永逸地加以证明了之后,则没有这同一个命题也就是一个完全的论证并且在形式上也是正确的。还有无数其他更复杂的链,不仅因为有更多的简单三段论进入其中,而且还因为作为其构成要素的那些三段论彼此之间更加不同,因为我们可以加入其中的不仅有简单直言的,而且还有连接的(copulatifs),也不仅是直言的,而是还有假言的;又不仅是完全的三段论,也还有省略三段论,其中被认为显然自明的命题是被省略了的。所有这一切,再加上非三段论的推论和命题的移位,以及大量的转折和想法由于心灵要求简短的自然倾向以及由于语言在质词的运用中部分地表现出来的那些特性而掩盖了这些命题——所有这些结合起来就将造成一条推理的链,它表现着一位演说者的全部论证本身,只是剔除和剥掉了它的装饰而还原为逻辑的形式,不是以经院的方式,但对于依照逻辑的规律来认识其力量永远是足够的,这种逻辑的规律,无非就是健全理智(le bon sens)的规律被安排成秩序并书写成文了而已,它和健全理智的规律的区别,也不过就像一种乡土风俗习惯,本来未书写成文的,现在书写成文了,这时和它原来未书写成文时的区别一样,只除了它既经书写成文并能更好地一下看出,就提供了更多的光明,使它能被推进和应用;因为自然的健全理智,要是没有技术的帮助,在作某些推理的分析时,有时对认识那些推论的力量会有点困难,例如就难于发现其中所包含的就真理来说是正确的但通常很少用的某个式。但一个逻辑学家,如果要人不用这样一些推理的链,或者他自己想不用这些,认为永远应该把一切复杂的论证都还原为它们实际所依据的那些简单的三段论,那就会像我已对您说过的那样,好比一个人向商人买了点东西,硬逼着商人要一个一个给他计数,就像扳着手指头来数数,或数城市大钟的钟点那样;这样,要是他不会别样算法,或要是他不是扳着手指头就不知道五加三等于八,那就表明他的愚蠢;或者如果他知道这些简便算法而不想用它或不许别人用它,那就表明是一种任意胡闹。他也就像一个人,不要人运用已经证明了的定理和公理,认为永远应该把一切推理都还原为这些中介的定理所实际依据的、能看出观念的直接联系的那些最初原则。
在解释了逻辑形式照我认为人们应采取的方式的用途之后,我来谈谈您的一些考虑。我看不出,先生,怎么您会以为三段论只能用来看出在单独一个例子中证据之间的联系。说心灵永远很容易看出结论,这是不会这样的,因为人们有时看到(至少在别人的推理中),那结论中首先是有可怀疑之处的,要是没有看到那推证的话。通常人们用一些例子来证实这些结论的正确,但这办法不是永远十足可靠的,虽然有一种技术来挑选例子,这些例子要是那结论不正确就不会被发现是真的。我不相信在管理得很好的经院中会允许毫无羞耻地否认观念间显然的符合,我也没有看到人们用三段论来表明这种符合。至少这不是它唯一和主要的用途。人们会比所想的更经常地发现(在考察那些作者的谬误理论时),他们是违犯了逻辑规则,而我自己就有这样的经验,有时在和一些有善意的人进行争论甚至笔头的争论时,只有用形式的论证把推理中的混乱消除了才开始让人了解了自己的意思。在一些深思熟虑的问题上想照经院哲学那样的方式来论证无疑会是可笑的,因为这种推理方式冗长得令人讨厌和非常麻烦,也因为这好像是扳着手指头来数数。可是,在那些有关人生、国家、拯救的最重要的深思熟虑问题上,人们常常让自己被权威的分量、被雄辩的微光、被举得不恰当的例子、被一些错误地假定被省略的命题是自明的那种省略推理,以及甚至被一些错误的结论弄得晕头转向,这一点只能说太确实了,以致一种严格的逻辑,但和经院中的逻辑是不一样的另一码事,对他们只能说是太必要了,除了别的之外,就有必要用它来决定哪一边是最显得正确的。此外,平常人并不知道人为的逻辑,却也还是能很好进行推理,甚至有时比受过逻辑训练的人还进行得更好,从这一点并不能证明逻辑无用,也正如我们不能因为看到有些人并没有学过读书写字,也不知道怎样用笔和筹码,在通常场合却能很好计算,甚至还能纠正另一个学过计算,但可能疏忽或弄混了数字或符号的人犯的错误,就证明人为的算术无用一样。的确三段论也可能变成诡辩,但三段论本身的规律正可用来认清这些诡辩;三段论也并不能使人转变信仰,甚至也并不永远能说服人,但这是因为那些区别的滥用以及那些没有被很好理解的名词把它们的应用弄得太冗长,甚至要是把它推到极端的话就变得令人难以忍受。
这里我只剩下要来考虑和补充您提出的那个论证了,那就是您用来作为一个不用逻辑学家的形式也很明白的推理的例子的。上帝惩罚人(这是一件被假定的事实);上帝公正地惩罚他所惩罚的(这是人们可以当作已经得到推证了的一条理性真理);因此上帝公正地惩罚了人(这是一条三段论的结论,被非三段论地扩充为a recto ad obliquum[4]),因此人是公正地受惩罚的(这是一种关系的戾换,但由于其自明而被省略了的);因此人是有罪的(这是一个省略三段论,这里省略了这样一个命题,它其实只是一个定义:凡是公正地受惩罚的是有罪的);因此人本来是能够以别的方式行事的(这里省略了这个命题:凡是有罪的,是能够以别的方式行事的);因此人曾是自由的(这里又省略了:凡是本来能够以别的方式行事的曾是自由的);因此(据自由的定义)他是曾有自行决定的能力的;这是需要证明的。我还注意到这因此本身其实既包含着那省掉未说的命题(即凡是自由的是有自行决定的能力的),又可用来避免名词的重复。而在这意义下,就什么也没有省略掉,并且那论证在这方面可以被当作是完全的。我们看到这论证是一条三段论的链,是完全符合逻辑的;因为现在我不想来考虑这推理的实质内容,在这方面也许是有些意见可提或可以要求作些阐明的。例如,当一个人不能够以别的方式行事时,在有些情况下他也可以在上帝面前是有罪的,好比他如果为了有某种借口不能援助他的邻人却就因此很高兴的话。总起来说,我承认经院式的论证形式通常是不适当的,不充分的,处理得不好的,但我同时要说,没有什么比依照真正的逻辑的形式论证的技术更重要的了,这就是说,就内容实质说是充分的,就推论的次序和结论的力量说是明白的,或者是本身自明的,或者是先已证明了的。
§5.斐 我曾认为在概然性方面,三段论是更少用处或者毋宁说绝对没有任何用处的,因为它只推进单单一个推论论证[5]。但我现在看到永远必须切实地来证明那在推论论证本身之中的可靠的东西,即在其中所发现的概然性,并看到结论的力量是在于形式之中。§6.可是,如果说三段论对于作判断是有用的,我还是怀疑它们能用于作发明,即找到证据和作新的发现。例如,我不相信欧几里得书上第一卷第47个命题的发现,当归功于通常的逻辑的规则,因为人们是首先认识了它然后才能以三段论的形式来加以证明。
德 把三段论的链以及一切我称为形式论证的也都包括在三段论之列,我们可以说,那不是本身自明的知识,是通过推论的结论而得来的,这些推论的结论只有当它们具有适当的形式时才是正确的。刚才说的那个命题,就是说直角三角形斜边的平方等于另两边的平方之和,在证明这个命题时,是把那大的正方形分成几块,并把两个小的正方形也分成几块,而发现两个小正方形的各块都可以在那大正方形里面找到,并且既不多也不少。这是相等的形式上的证明,而各块的相等也是用有正确形式的论证来证明的。古代人的分析,照巴波[6]说是取其所要求解决的,然后从之引出结论,直至达到某种给定的或已知的东西。我曾指出,为了达到这个结果,那些命题必须是可相互换位的,以便那综合的证明能通过分析的途径又倒回到相反方向去,但这永远是引出结论。可是这里指出这一点是好的,即在天文学或物理学的假说中,这种逆转是不行的;但成功也并不证明假说的真实性。的确它使之成为概然的,但由于这种概然性似乎显得违反了逻辑上教人的真的也可以从假的引出这一条规则,人们会说逻辑规则在概然问题上将完全没有什么作用。我回答说,真的会是从假的所引出的结论,这是可能的,但并不是永远概然的,尤其当一个简单的假说为许多真理提供理由时是这样;这是很罕见并且很难碰到的。我们可以和卡尔唐[7]一起说,概然的逻辑有和必然真理的逻辑不一样的结论。但这些结论的概然性本身应该是用必然真理的逻辑的结论来加以证明的。
§7.斐 您似乎是在为普通逻辑作辩护,但我看得清楚您所提出的是属于一种更高级的逻辑的,普通逻辑对于它来说,就好比初级的ABC对于学者的广博学识一样;这使我记起贤明的虎克[8]的一段话,他在他的名叫《教会政治》一书的第一卷§6.中认为,如果人们能够提供一些对知识和推理技术的真正帮助,这在我们这个算是开明的时代是不大为人所知并且人们也不大为它费心的,那么在判断的成熟可靠方面,用了这些帮助的人们和现在的人们之间就会有很大的区别,正如现在的人们和那些无知的傻瓜之间的区别一样大。我希望我们的谈话能给一些人以机会,来发现这位具有如此透辟精神的伟大人物所说的这些对技术的真正帮助。这将不是一些模仿者,像牲畜跟着脚印走老路那样的(imitatorum servum pecus[9])。但我敢说,在这个时代是有一些人有这样的判断力和这样广阔的心灵,以致能够找出一些新的途径来促进知识的,如果他们愿意费心把思想转向这一方面的话。
德 您已经和已故的虎克先生一起很好指出,先生,世人不大在这方面用功夫;否则我相信是有并且已经有过一些人能在这方面获得成功的。不过必须承认,我们现在是有一些重大的帮助的,不论在数学或在哲学方面都一样,在这方面您那位卓越的朋友的《人类理智论》就不是最小的。我们将来看看是否有办法从之得益。
§8.斐 我还得对您说,先生,我本来曾认为在三段论的规则中是有一种显然可见的错误的;但从我们在一起谈话以来您已使我迟疑起来了。可是我还是要向您提出我的困难。人家说,“任何三段论的推理,如果不包含至少一个全称命题,就不能有结论”。但似乎只有特殊事物才是我们的推理和我们的知识的直接对象;它们只涉及观念的符合不符合,这些观念每一个都只有一种特殊的存在并且只代表一件单个的事物。[10]
德 只要您想到事物的相似性,您就想到了某种不止于此的东西,而普遍性无非就在于此。您也永远不会提出任何论证,其中没有用到普遍真理的。可是指出这一点是好的,即人们是把(就形式方面说)特称命题包括在全称命题之下的。因为虽然的确只有过单单一位使徒圣彼得,我们却可以说,凡曾是使徒圣彼得的都曾不认他的主。这样,这个三段论:圣彼得曾不认他的主,圣彼得曾是一个门徒,因此有些门徒曾不认他的主(虽然只有特称命题),是被看作具有全称肯定命题的,而它的式将是第三格中的Darapti。[11]
斐 我还想告诉您,我本来觉得把三段论的两个前提的位置换一下,说所有A是B,所有B是C,因此所有A是C,比之于说所有B是C,所有A是B,因此所有A是C,似乎更好些。但照您所说的看来,这样似乎也差不多,而两者是被算作同一个式的。如您所指出那样,和通常不同的那种安排法更适合于作成多个三段论构成的一条链,这总始终是真的。
德 我完全同意您的意见。可是人们似乎曾认为像第一格和第二格的大前提那样从全称命题开始,是更适合于教授法的;而且现在还有些讲课者有这种习惯。但像您提出的那样那联系是显得更清楚。我以前曾注意到亚里士多德可能是有一种特殊的理由要照通常那种排法。因为他不说A是B而习惯于说B在A中。而照这种说法,则您所需求的那种联系本身在他就出现在通常所接受的那种排法中了。因为他将不说B是C,A是B,因此A是C,而是这样说:C在B中,B在A中,因此C在A中。例如,不说:矩形是等角形(即各角相等的),正方形是矩形,因此正方形是等角形,亚里士多德不改变命题的位置,而把中间位置保留给中词,用把名词的位置倒过来的办法来说这些命题,他会说:等角形是在矩形之中,矩形是在正方形之中,因此等角形是在正方形之中。而这种说法是不应加以轻视的,因为实际上谓词是在主词之中,或者说谓词的观念是包含在主词的观念之中的。例如,等角形是在矩形之中的,因为矩形是所有的角都是直角的图形,而所有的直角都是彼此相等的,因此在矩形的观念中就有一个所有的角都相等的图形的观念,而这就是等角形的观念。通常的说法毋宁是对个体来说的,但亚里士多德的说法则更多的是就观念或共相来说的。因为说所有的人是动物,我是想说所有的人是包含在所有的动物之中的;但我同时也理解为动物的观念是包含在人的观念之中的。动物比人包含着更多的个体,但人则包含更多的观念或更多的形式性[12];一个有更多的例子,另一个有更大程度的实在性;一个有更大的外延,另一个有更多的内含。我们也可以真正地说,全部三段论都可以用de continente et contento[13]即包含者和被包含者的理论来加以证明,这和全体与部分的理论是不一样的;因为全体永远是大于部分的,但包含者与被包含者有时是相等的,如在可相互换位的命题的情况就是这样。
§9.斐 我开始对逻辑形成了和以往我对它的观念完全不同的另一种观念。我本来把它当作是一种学者的游戏,而我现在看到它照您所理解的那样好像是一种普遍的数学。但愿上帝保佑人们能把它加以推进,使它成为某种胜过它现在所处状况的东西,以便我们能找到虎克所说的那种对理性的真正帮助,这将使人们提高到远远超出当前状况之上。而理性是非常需要这种帮助的一种功能,它的范围是十分有限的,并且它在很多方面对我们是有缺陷的。这就是(1)因为往往那些观念本身就是我们所缺乏的。§6.然后(2)这些观念往往又是模糊和不完全的;反之在它们是明白清楚的场合,如在数的情况,我们就不会发现不可克服的困难,也不会陷入任何矛盾。§7.(3)困难也往往来自我们缺乏中介观念。我们知道,在代数这种重大的工具和人类机智的显著证据被发现以前,人们看到古代数学家们的许多推证都很惊讶。§12.也有这种情况,(4)人们在一些假的原则的基础上来建立〈理论〉,这就可能陷入困难,在这里理性只有进一步把事情弄乱而远不是把事情搞清楚。§13.最后,(5)那些意义不确定的名词,使理性为难。
德 我不知道我们是否如您所想那样缺乏那么多观念,这是说,清楚的观念。至于混乱的观念,或毋宁说影像,或者要是您喜欢,可以说印象,如颜色、滋味等等,这是许多小观念的一种结果,这些小观念本身是清楚的,但我们不能清楚地察觉到,这样的观念有无数是我们所缺乏的,这些观念对别的生物比对我们更适合。但这些印象也毋宁只是有助于产生一些本能和建立起一些经验的观察,而不是为理性提供材料,除非是它们伴随着清楚的知觉。因此主要是我们缺乏对这些被混乱观念掩盖着的清楚观念的知识,阻碍了我们,而甚至当一切都清楚地陈列在我们感官或我们心灵面前时,那必须考虑的事物的繁多,有时也把我们搅浑。例如,当有一千发的一堆炮弹放在我们眼前时,显然,为了能够很好地想着这很多的一堆东西的数目和特性,把它们像在仓库里所干的那样安排或各种形状是很有用的,为的是对它们可以有清楚的观念,并且甚至将它们加以固定,这样就可以省去麻烦,不必屡次地来数它们。也正是考虑的东西的繁多,使得在关于数本身的科学中也有一些极大的困难,因为人们在其中找一些简便的办法,而有时不知道自然对所涉及的情况是否在它夹缝中有这样的办法。例如,表面看起来还有什么比素数的概念更简单的吗?所谓素数就是指除了1和本数之外不能被任何其他数所整除的整数。可是人们还在寻找一种确实而容易的标志,以便用不着把小于所给定素数的平方根的所有〈各个本身也是〉素数的除数都来试一试,就能确定地认识这些素数。有大量的标志,可以使人不必作很多计算就知道某个数不是素数,但人们要求要有一种标志,既是容易的,又当一个数是素数时就能使人确定地知道它是素数。也正是这使得代数学至今还是如此不完善,虽然没有什么比它所用的那些观念更为人所知的了,因为这些观念无非是指一般的数;因为公众至今还没有办法来求出超过四次的任何方程的无理根(只除了一种极受限制的情况),[14]而刁方廷[15]、斯齐比翁·费利[16]以及路易·费拉利[17]各自用来求解二次、三次和四次方程的方法,目的是把它们化为一次方程,或者是把带从方程[18]化为纯方程,这些方法彼此都是完全不同的,就是说,用来解某一次方程的方法和用来解另一次方程的方法差一次。因为二次方程化为一次的,只要消去那第二项就行了。三次方程的得到解决是因为把未知数分成几部分,由此就幸好得到了一个二次方程。而在四次或双二次的方程中,是在方程的两边加上某种东西,以使得两边都能开方;而又幸好发现要得到这个结果,只需要一个三次方程就行了。但所有这一切都只是幸运或机遇和技术或方法的一种混合。而在探索后两种即三次和四次方程的解法时,人们并不知道它是否能成功。在五次或六次即双三次的方程方面要获得成功,也还需要某种别的技巧;而虽然笛卡尔曾认为,他在解四次方程中所用的方法,即把四次方程看作另外两个二次方程所产生的结果(但这方法归根到底也并没有超出路易·费拉利的方法),在解六次方程中也会得到成功,却并没有被发现是这样。这种困难使人看到即使最明白、最清楚的观念也并不始终总是给我们所要求的一切和从它们能得出的一切。这也使人断定,代数要成为发明的技术还差得很远,因为它本身也还需要一种更一般的技术;而我们甚至可以说,那种普遍语文(la specieuse en général[19])即关于符号的技术对此是一种了不起的帮助,因为它有助于解放想象力。看了刁方廷的算术和阿波罗纽及巴波的几何学书籍,我们毫不怀疑古代人在这方面已有了一些东西。韦达[20]曾对此加以扩大,不仅要求的未知数而且连已知数也用一般的字母符号来表示,在计算方面作了欧几里得在推理方面所已做的事;而笛卡尔则把这种计算扩大应用于几何学,用方程来表示线。可是即使在我们现代的代数学发现以后,布依奥先生[21],无疑是一位卓越的几何学家,我在巴黎也曾认识的,也看到阿基米德关于螺线的证明只感到很惊奇,而不能理解这位伟大人物怎么会想到把这曲线的切线作为圆的度量。而圣·文生的格里高利神父[22]似乎猜到了这一点,断定这是由螺线和抛物线的类似而达到的。但这条途径只是一种特例,而我所想到并且成功地与公众分享的那种通过微分法来进行的新的无穷小演算[23],则给了人一种一般的方法,在这里,这种就螺线所作的发现就只是一种游戏和最容易的事情的一种试样,就像我们以前在有关曲线长度问题方面所曾发现的几乎所有东西一样。这种新的演算之所以有好处,其理由还在于它在笛卡尔排除在他的几何学之外的那些问题上解放了想象力,笛卡尔排除这些问题的借口是说它们最经常地会引向力学去,但骨子里是因为它们和他的演算不一致。至于那些由于名词的含糊而产生的错误,那是要靠我们去加以避免的。
斐 也还有一种情况是不能用理性的,但这里也是不需要理性并且观察的眼光比理性还更有价值的。这就是在直觉知识方面的情况,这里观念之间和真理之间的联系是直接被看到的。对那些无可怀疑的公则的知识就是这样,而我总倾向于认为,这是天使现在所具有,也是达到完美程度的正义的人的心灵在未来状态下对于现在为我们认识所不及的千百种事物所具有的显明性的程度。§15.但基于中介观念的推证,则给人一种推理知识。这是因为中介观念和两端观念的联系是必然的,并且通过明证的并列而被看到的,就好像一根尺子,我们用来量一下这件衣服,又量一下那件衣服,以使人看出它们是一样长的。§16.但如果那联系只是概然的,则判断只给人一种意见。
德 单只上帝才有只具有直觉知识这种好处。但那些幸福的灵魂,不论如何脱离了这粗鄙的身体,以及那些精灵本身,不论他们何等崇高,尽管他们具有一种比起我们的来无比地更为直觉的知识,并且往往一眼就能看出我们靠推论的力量在花了许多时间精力以后才能找出的东西,他们在他们的道路上也当碰到困难的,否则他们就会没有作出发现这种愉快了,这是最大的愉快之一。并且永远应该承认也有无数真理对他们也是掩盖着的,或者是完全掩盖着,或者是一时掩盖着,须要他们靠推论的力量才能达到,也要靠推证或者甚至往往还靠猜测。
斐 〔那么这些精灵也就只是比我们更完善些的动物了,这就好像您和那位月亮上的皇帝一起说过的,一切也都和这里地上一样。〕
德 我要说不是完全这样,而是就事物的根底来说是这样,因为圆满性的方式和程度是无限地变化多端的。可是那根底是到处同样的,这在我是一条基本公则,并且支配着我的全部哲学的。而我只是照我们所清楚认识的事物的方式来设想那些不认识或混乱地认识的事物;这使得哲学成为非常容易的,而我确认为是应该这样。但如果说这种哲学就根底来说是最简单的,而就表现样式方面来说则也是最丰富的,因为自然可以使它们无限地变化多端,正如它也使之具有所能想象的一切富饶、秩序和装饰一样。就是因为这样,我认为没有什么精灵,不论他如何崇高,会没有无数更高的精灵在他之上。可是虽然我们比这许多精灵性的存在物低得多,我们却有这种好处,就是在这地球上并不显然受控制,在这里我们是毫无争议地占有头等地位的;而且不论我们陷于怎样的无知状态,我们却有这样的愉快,没有看到什么超过我们之上的。而如果说我们这样是虚荣,我们也可以像恺撒那样认为,宁愿在一个小村镇当头头,也不愿在罗马当第二把手。此外,我这里说的只是这些心灵的自然知识,而不说那种有福的面见上帝[24],也不说上帝愿赐给他们的那种超自然之光。
§19.斐 由于每个人都或者对自己或者对别人来运用理性的推理,对于那四种论证来作些思考将不是无用的,人们习惯于用这论证来把别人拉到自己的意见这边来,或者至少是使别人处于一种折服状态,以阻止他们进行辩驳。第一种论证可以叫做argumentum ad verecundiam,[25]当人们引用那些由于知识、地位、权力或其他而获得权威的人的意见时就是这样;因为当别人不立即顺从它时,就会被谴责为虚荣浮夸,甚至被责为傲慢无耻。§20.还有(2)argumentum ad ignoratiam[26],这就是迫使对方承认那证据,否则就要他指出一个更好的来。§21.还有(3)argumentum ad hominem,[27]当人们以一个人自己说过的话来逼迫他时就是这样。§22.最后还有(4)argementum ad judicium[28],这就是应用从某种知识或概然性的源泉得出的证据〈来进行论证〉;而这是所有论证中唯一能使我们前进和对我们有所教益的;因为假使我出于恭敬而不敢反驳,或者我没有什么更好的可说,或者我自相矛盾了,也并不因为这些您就是对的。我可以是谦逊的,无知的,弄错了的,而您可能也是弄错了的。
德 在说起来是对的和真正要来相信的东西之间,无疑必须加以区别。可是,大部分的真理是可以大胆公开地坚持的,有些反对一种意见的偏见却必须遮遮掩掩。利用无知(ad ignorantiam)的论证在一些要作出推定的情况下是对的,在这种场合,坚持一种意见直到那相反的得到证明为止,是有道理的。以子之矛攻子之盾(ad hominem)的论证有这样的效果,即它表明这一个或另一个论断是假的,而对手不论采取何种方式总是错了的。我们还可以提出人们所用的其他一些论证,例如那可叫做ad vertiginem[29]的论证,当人们像下列这样推理时就是这种论证:如果不接受这一证据,我们就无法在所论之点上达到确定性,这是被人看作荒谬的。这种论证在某些情况下是对的,好比有人若想否认那些原始的直接的真理,例如任何东西都不能同时既是又不是,或我们自身存在[30],因为如果他有理,那就会没有任何办法来认识任何东西。但当我们定下某些原则,并想加以坚持,因为否则已被接受的某种学说的整个系统将会倒塌时,这论证却不是决定性的;因为在那必须用来支持我们的知识的东西,和可用来作为我们已被接受的学说或我们的实践的基础的东西之间,必须加以区别。在法学家们那里有时就用一种类似的推理来为他们根据其他被控犯有同样弄妖术罪的人的供词而对那些被认为弄妖术的人定罪或刑罚的做法进行辩护,因为他们说:如果这一论证倒台了,那我们怎么来使他们服罪呢?而有时在刑事问题上,某些作者以为在较难使人服罪的事情上,比较薄弱的证据也可以被当作充足的。但这不成一个理由。这只是证明必须更加仔细小心,而不是说我们应该更加轻忽地就相信,除非是在一些极端危险的犯罪案件中,例如在大逆不道的事情上,这种考虑是有分量的,不是为了给一个人定罪,而是为了防止他为害;这样,在判决中,在法律和习惯许可的场合,就可以有一种中道,不是在有罪与无罪之间的中道而是在定罪与免罪之间的中道。在德国,若干时期以来人们也用一种类似的论证来为铸造坏钱币文过饰非;因为(他们说)如果要遵守规定的规则的话,我们要铸钱就不能不有所损失。因此就应该允许降低成色。但除了应该只减轻重量而不是降低成色或成分来更好地避免作假骗人之外,人们是把一种并非必要的做法当作必要的;因为既没有上天的命令也没有人间的法律要强迫那些既无矿产也没有机会有许多银条子的人来铸造钱币;而将钱求钱,这是一种很坏的做法,它自然会带来腐化堕落。那么(他们说)怎么来实施我们铸钱的王家特权呢?答案是很容易的。你就满足于用好银子少铸点钱币吧,即使受点损失也罢,要是你认为铸钱造币对你很重要的话,因为你既无必要也无权利以坏货币来充斥世界。
§23.斐 在关于我们的理性和其他人的关系方面说了一点之后,让我们再就它和上帝的关系再来说一点,这种关系使我们在那反理性的和超理性的之间作了区别。属于第一类的是一切和我们明白而清楚的观念不相容的东西;属于第二类的是一切这样的想法,它的真实性或概然性是我们看不出能借助于理性从感觉或反省演绎出来的。因此如不止一位上帝存在是反理性的,而死人复活是超理性的。
德
关于您对超理性的所下的定义,我觉得有点意见要提,至少要是您把它和这话的公认用法联系起来的话;因为我觉得照这定义所暗示的方式,它一方面走得太远了而另一方面又走得不够远;而如果我们遵照着它,则凡是我们所不知道的以及我们在当前状况下没有能力认识的东西就会都是超理性的了,例如,某一恒星比太阳大些或小些,还有维苏威火山在哪一年将会爆发喷火,这些事实的知识超出我们的范围,并不是因为它们是超乎我们的感官的;因为我们要是有更完善的器官并且对其环境情况有更多了解的话,是将能很好地对它作出判断的。也有一些困难,是超乎我们现在的功能,但并不是超乎一切理性的;例如,世上没有一位天文学家能够不用握笔在手就计算出在一个pater[31]的空间的一次日月食的细节,可是也许有些精灵,对他们来说这简直不过是一种儿戏。因此,所有这些事情,假定有对事实更多的了解,更完善的器官和更高级的心灵的话,都可能被弄成借助于理性得以认识或可行的。
斐 要是我把我的定义理解为不仅是对我们的感觉或反省,而是也对所有其他可能的被创造心灵的感觉或反省而言,那您这反驳就失效了。
德 如果您这样理解,您是对的。但将还有另一个困难,这就是:照您的定义就将没有什么是超理性的了,因为上帝将永远能够给办法用感觉和反省来把握不论什么真理;正如事实上那些最大的神秘事情由于上帝的作证对我们也就变成被认识的了,这种作证是我们通过可信性的动机(les motifs de crédibilité)而认识到的,我们的宗教就以这种动机为基础。而这些动机无疑是依赖于感觉和反省的。因此问题似乎不在一件事实的存在或一个命题的真实性是否能从理性所用的原则,也就是从感觉和反省,或者说从外感官和内感官演绎出来,而在于一个被创造的心灵是否能够认识这事实的如何或这种真实性的先天理由;所以我们可以说那超理性的也是很能被把握的,但它是不能通过被创造的理性的途径和力量而被理解的,不论这理性多么伟大和崇高。这是单只保留给上帝来理解的,正如使它成为事实也单只属于他一样。
斐 这种考虑我觉得是对的,我也正是希望人家这样来理解我的定义的。这同一种考虑也使我更坚信我现在所持的意见,即把理性和信仰对立起来的说法,尽管有很大权威,也是不恰当的,因为我们是用理性来核实我们所当信仰的。[32]信仰是一种坚决的同意,而得到应有方式的规范的同意,只能是根据正当理由来给予。因此那种并无任何相信的理由就相信的人,可能是爱他的幻想,但他并不是真的在追求真理,也不是合法地服从他神圣的主,主要是他运用那些功能的,主以那些功能丰富了他,为的是保他不犯错误。否则,如果他走在正路上,那是碰巧;而如果他走了邪路,那是由于他的错误,对此他是要对上帝负责的。
德 我非常赞赏,先生,您要把信仰建立在理性的基础上;要不然为什么我们会认为基督教圣经比可兰经或婆罗门教的古籍好呢?我们的神学家们以及其他一些有学问的人也都曾认识到这一点的,也正是这一点使得我们有如此美好的有关基督教真理的作品,并且有这么多美好的证据被提出来反对那些异教徒以及古代和近代的其他不信神的人们。明智的人们也始终怀疑那样一些人的主张,他们以为在涉及信仰的事情上是不必费心考虑理由和证据的;其实这是不可能的事情,除非信仰就只意味着背诵或重复,以及无所用心地听之任之,就像很多人所干的那样,以及甚至就像有些民族的性格那样,他们比其他民族更其如此。这就是为什么十五和十六世纪的有些亚里士多德派哲学家,他们的残余在那以后很久还继续存在(如我们从已故的诺德先生[33]的信及《诺德集》中可以看出的),曾想主张有两种对立的真理,一种是哲学的,另一种是神学的,在利奥十世主持下的最后一次拉特兰会议[34]曾有理由加以反对,正如我认为已曾指出过的那样。[35]前些时在赫尔姆斯台特,在神学家但以理·霍夫曼(Daniel Hoffmann)和哲学家高乃伊·马丁(Corneille Martin)之间也曾引起过一场完全类似的争论,不过有这点区别,这位哲学家是要把哲学和启示相调和,而这位神学家则想抛弃哲学不用。而儒勒公爵(le Duc Jules),这位大学的创立者,则宣布支持哲学家[36]。的确,在我们的时代一位有最崇高地位的人士也说过,在信仰问题上必须挖掉眼睛才能看得清楚,而德尔都良[37]在有个地方也说过:这是真的,因为它是不可能的;这是必须信仰的,因为它是荒谬的。但如果说这样说法的人心意是好的,这种说法总是过头的,并且可能造成危害的。圣保罗就说得更正确些,他说上帝的智慧在人面前是疯狂;这是因为人们只是照他们极其有限的经验来判断事物,而凡是和这经验不合的在他们就显得是荒谬的。但这种判断是非常冒失的,因为有无数自然事物,要是别人对我们说起的话,我们也会当它们是荒谬的,就像有人说我们的河面上盖着冰,那位暹罗国王就觉得是荒谬的一样。但自然本身的秩序,既不是什么形而上学的必然性,就只是基于上帝的乐意,所以是可以由于神意的高超理由而远离这种秩序的[38],虽然他也完全只应根据正确的证据行事,这种证据只能来自上帝本身的作证,对此,当其得到恰当证实时,我们是应该绝对恭顺服从的。
[1]法语raison或英语reason一词,有多种含义,中译通常在不同场合因其不同含义分别译作“理性”或“理由”等等。这里用的这个词也涉及多种含义,但为表明它在原文中是同一个词,故一律译作“理性”。
[2]参阅本书第二卷第十四章§27“德”;第十七章§1“德”。 这里的“理性”即raison,都本可译作“理由”,下同。
[3]莱布尼茨在1663年大学毕业时的学位论文答辩就是讨论这个原则,题为Disputatio metaphysica de principio individui(《个体性原则的形而上学答辩》),载G本第四卷第15—26页,E本第1—5页,即第一篇。 拉丁文,意即:“由正到歪”,或“由直到曲”。
[4]Héliogabalus,218—222年为罗马皇帝,以愚蠢、残暴和荒淫无道著名。 见上第589页注①。
[5]三个都是《圣经》里的人物,该隐(Cain)是亚当和夏娃的长子;含(Cham,英文作Ham)是挪亚(Noé)的第二个儿子,被说成是黑种人的祖先,伊斯梅尔已见前注,被说成是阿拉伯人的祖先。 原文为argument topique,亚里士多德的《正位篇》(les Topiques)1.,1,100a27以下,说明“argument topique”是指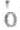 διaλεκτικ
διaλεκτικ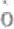 ς συλλογισμ
ς συλλογισμ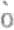 ς或
ς或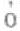
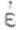 ξ ενδ
ξ ενδ ξων συλλογιζ
ξων συλλογιζ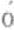 μινος,即“辩证的三段论”或“从概然的出发进行推理的三段论”,以区别于
μινος,即“辩证的三段论”或“从概然的出发进行推理的三段论”,以区别于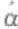 π
π δειξις,即基于和引回最初的必然真理的证明。
δειξις,即基于和引回最初的必然真理的证明。
又参阅第二卷第二十一章§66“德”(2)注(第207页注②),及第四卷第一章§1“德”注(第414页注②)。
[6]原文各本均作§9,但下面又有§9,当系§8之误。在洛克原书此段内容也见8。 见前第四卷第十二章§4“德”注(第547页注③)。
[7]法文原文为“sentiment”,英译作“consciousness”。 见第一卷第一章开始处的注(第33页注④)。
[8]G本原文作:“la conscience(consciousness ou connscienciosité)”,E本及J本作“la conscience(consciousnes ou consciosité)”。 Richard Hooker,1553—1600,在他所作的《教会政治的法律》(Laws of Ecclesiastical Polity)一书中,企图维护新教君主和国会所建立的那种对英国教会的主教制形式的统治,而反对长老会派对此的攻击。为此目的,他在该书的头两卷中提出了一些基本原则作为解决所争论的问题,特别是关于一般法律本性问题的哲学基础。洛克和莱布尼茨所引的这一段,见该书第一卷第六章§3。见牛津大学1841年版《虎克著作集》两卷本的第一卷第164页。
[9]“不休”原文为“incessabilité”,直译即“不可停止性”,即永久继续下去的意思;“不朽”原文为“immortalité”,也就是“不死”。照莱布尼茨的观点,不论是动物或人的灵魂,作为“单子”都是不能自然消灭的,也就是不死的;他甚至还否认任何生物有严格意义的“生”和“死”,可参阅《单子论》§73及§14等处。 拉丁文,意即:“模仿者,供人役使的牲畜”,见贺拉西Epist.(《书信》)1,19,19。
[10]“不休”原文为“incessabilité”,直译即“不可停止性”,即永久继续下去的意思;“不朽”原文为“immortalité”,也就是“不死”。照莱布尼茨的观点,不论是动物或人的灵魂,作为“单子”都是不能自然消灭的,也就是不死的;他甚至还否认任何生物有严格意义的“生”和“死”,可参阅《单子论》§73及§14等处。 这里是洛克的经验论中唯名论观点的鲜明表现。这种观点只承认单个或特殊事物的存在,而否认普遍性的实在性,从而也只承认对单个事物的认识而否认对普遍性的理性认识的可靠性。这也正是洛克这种经验论观点的片面性和局限性所在。莱布尼茨对这种观点的反驳是抓住了经验论固有的弱点的,但他自己的观点则是唯心主义的,同时他的唯理论观点总的说来也陷于另一方面的片面性。
[11]Darapti即第三格第一式,参阅第四卷第二章§1“德”注(第423页注②)。
照通常的办法,这里“彼得”作为中词,而“门徒”是结论中的主词,小前提必须换位,这样全称肯定命题“圣彼得曾是一个门徒”就变成了特称肯定命题“有些门徒曾是圣彼得”,从之就直接可得出特称肯定的结论“有些门徒曾不认他的主”。这样第三格的Daraptj式就变成了第一格的Darii式。这里前提之所以为全称是因为“彼得”构成他所属的整个的类,其实也就是把“彼得”看成只包含单个分子的“类”。关于“彼得不认主”,见《马太福音》第二十六章第六十九节以下。
[12]formalités,经院哲学名词,即指本质。
[13]拉丁文,意即:“包含者和被包含者”。
[14]G本和J本作“les âmes estant...”(J本作étant),E本作les ames tant...,译文从G本和J本。 在莱布尼茨的时代,如正文所说,二次、三次、四次方程都被化为纯方程,而超过四次的更高次方程的化法,还是个未解决的问题,数学家们为此费了很多工夫,直到挪威的著名数学家阿贝尔(N.H.Abel,1802—1829)才证明了(1824)五次及任何更高次的方程一般都不可能以根式来求解。
[15]Henry More,拉丁名Morus,参阅第一卷第一章(第33页注⑧)。他认为一切灵魂都是和这世界同时被创造出来的,并且和莱布尼茨一样认为灵魂也是永远和某种物质相结合的,参阅他的《著作集》第1卷,第750—754页。 Diophantus,约325—409,亚历山大里亚学派的著名希腊数学家,在其《算术》一书中曾给出了解一次和二次方程的方法。
[16]Messie,英文作Messiah,一译“默西亚”,即“救世主”,古代犹太人“先知”预言上帝将派遣“救世主”来拯救世人特别是以色列人。基督徒则认为耶稣基督就是这“救世主”。 Scipion du Fer,或Scipione del Ferro或Ferri,约1465—1525,意大利数学家,约在1505年曾发现了一个三次方程的特例的解法。
[17]Louis de Ferrare即Ludovico或Luigi Ferrari,1522—1562或1565,意大利数学家,曾发现解三次方程的公式的证明,和解四次方程的方法。
[18]“带从方程”原文为équation affectée,疑是指具有低次项的方程。如费拉利解x4+ax3+bx2+cx+d=0时,就是设法先消去ax3,而如果ax3,bx2,cx都消去则得纯方程。我国古代称解纯三次方程为开立方,而称解一般三次方程为“开带从立方”,故姑且将“équation affectée”译为“带从方程”。
[19]G本和E本作“l'expression”(“表现”),J本作“l'impression”(“印象”)。 参阅第三卷第二章§1“德”(第302页注①),及三卷九章§19—21“德”(第390页注①)等处。
[20]见前第四卷第七章§6“德”注(第489页注①)。
[21]Bouillaud(Ismael Bullialdus)即Ismael Boulliau,1605—1694,法国的数学家和天文学家,曾对某些星的光的变化首先提出过一种解释。
[22]Grégoire de Saint-Vincent,1584—1667,法兰德斯的几何学家,曾大力从事于探求化圆为方的问题。
[23]从G本、E本和J本仍如前§9作(consciosité ou consciousnes)。 “微分法”,原文为différences,这词在现代是指“差分法”,但在莱布尼茨的时代是指“微分法”。“无穷小演算”原文为“calcul des infinitésimales”,也就是指莱布尼茨所发明的微分。关于他自己对他发明微积分一事的论述,可参考他的Historia et origo calculi differentialis(《微分的历史和起源》),载Gerhardt编《莱布尼茨数学著作集》Ⅱ.1〔第五卷〕,392—410;Dutens编的《莱布尼茨全集》第三卷有大量有关莱布尼茨和牛顿关于微积分发明权问题的争论的材料。
[24]vision béatifique,这是宗教神学上用的名词,用以指圣者和天使在天上直接面见上帝,这被认为是他们的主要幸福。这种观点本起源于柏拉图所宣扬的对理念的“超理性”的直觉知识,新柏拉图主义者斐罗、普洛提诺等进一步发展为对于上帝的神秘的出神状态的直观,中世纪基督教的一些神秘主义神学家特别宣扬这套观点。一些哲学上的唯心主义者也借此来宣扬一种“超理性”、实即反理性的而似乎是最确定、最完满的绝对知识。
[25]拉丁文,意即:“借口谦恭的论证”,洛克原书中译作“剽窃名言”。
[26]拉丁文,意即:“利用无知的论证”,洛克原书中译作“利用无知”。
[27]拉丁文,意即:“以子之矛攻子之盾的论证”,洛克原书中译作“穷迫他说”。
[28]拉丁文,意即:“明辨事理的论证”,洛克原书中译作“准事酌理”。
[29]E本和J本无“或宽恕”(ou excusé)。 拉丁文,意即:“兜圈子”〈的论证〉。
[30]G本原文作“juger contre ce qu'il sait?”;E本和J本作“juger contre ce qu'ils font?”(“作出和他们所做的事相反的判决”)。 E本无“ou que nous existons nous mêmes”(“或我们自身存在”)一句,译文从G本。
[31]拉丁文,这词的通常意义是指“父亲”,也指天上之“父”即“上帝”,或神话中的众神之王尤比德(Jupiter)。这里所谓“一个pater的空间”也就是指“广阔无垠的空间”的意思。
[32]Origène,185—253,出生于亚历山大里亚的基督教圣经注释家,神学家,早期的护教者,把柏拉图的学说和基督教义相融合。 这里照G本,原文为“car c'est par la raison que nous vérifions ce que nous devons croire”。E本和J本此句均作:“car c'est par la raison que nous devons croire”。(“因为我们应该凭理性来信仰。”)
[33]E本和J本无“完全”(entier)一词。 Gabriel Naudé,1600—1653,著名法国学者,初曾为法王路易十三的医生,后主要从事于文化及图书馆事业。《诺德集》(Naudenna)是从他的谈话中抽出的一些逸闻的集子。
[34]拉特兰(Latéran)是罗马天主教的大本营,这是指1512年12月19日在教皇利奥十世主持下的第五次拉特兰宗教会议。
[35]原文为l'angle de contingence,照字面的意义就是偶然的、不正规的或异常的角,实际是指切线与弧之间的角,有的数学家也称之为“号角状角”(horn-shaped angle),欧几里得几何学是把它作为不正规的角而要加以排除的。 参阅《神正论》前言,§§7、8、11。这里所说的“亚里士多德派哲学家”,分为两派,是按照其创始人对亚里士多德的不同解释而形成的。一派称“亚历山大派”,是照公元200年前后,阿发洛地西亚(Aphrodisias)的亚历山大(Alexandre)的解释,另一派称“阿威罗伊派”,是照伊斯兰哲学家阿威罗伊(Averroes,1124—1198,即伊本·鲁世德)的解释。两派都否认个人灵魂不死,也都主张“双重真理”说,因而在1512年的“拉特兰会议”上被定为“异端”。十五、十六世纪主张这种“双重真理”说的人中,最主要的是意大利哲学家彭波那齐(Pietro Pomponazzi 1462—1525)。他属于“亚历山大派”,也被控为“异端”,他曾企图为这种“双重真理”说找一种更深的基础,认为理性有双重的本性,即思辨的和实践的,思辨的理性提供了哲学的基础,实践的理性则提供了神学和伦理学的基础。这种“双重真理”说在当时是企图为哲学摆脱传统宗教神学的束缚寻找理论根据,因而具有反封建的进步意义的。
[36]参阅《神正论》,前言§13.关于这场争论,从1598延至1601年,可参阅Pünjer,Gesch.d.Christ.Religionsphilosophie(彭耶:《基督教宗教哲学史》)第一卷,第132—141页,以及托马修:《论霍夫曼的争论》(G.Thomasius:De controversia Hofmanniana,Erlangen,1844)等专著。本书德译者夏尔许米特注认为儒勒公爵是Henry Julius,是那位大学创立者儒勒公爵的儿子和继承人,他曾审阅了这场争论的文件,并作出决定,要保护哲学家而反对他的对手,这些对手就在国外大肆散布恶毒诽谤他的流言飞语,对他进行攻讦。(https://www.daowen.com)
[37]Tertullien,160—240,基督教早期的著名“教父”,生于迦太基。这里所引的他的话,见于他的De carne christi(《论基督的肉体》),第五章。莱布尼茨在其《神正论》前言§50,也引了这段话。
[38]Corlowitz或Karlovci是现今南斯拉夫的一个城市,1699年1月26日,土耳其在战败后与奥地利、波兰、威尼斯及俄国在此订立和约,放弃了大片在欧洲所占领土。这里所说“皇帝”当系指“神圣罗马帝国皇帝”,亦即奥地利的皇帝。 参阅第四卷第六章末的注(第483页注①)。
