6.3 线性规划
案例 风电场排班问题(2016高教社杯全国大学生数学建模竞赛D题第三问)
某大型风电场共有风机124台,4组工作人员,根据风电场实际风速、风机及工作人员的情况,解决以下最优风机维护排班问题:已知每台风机需每年进2次维护,为更好地养护风机,每台风机的连续工作时间不能超过270d;并且,每台风机每次维修需用时连续2d,为应变突发状况,风电场每天需留1组工作人员值班,因风电场地处郊区,考虑到工作人员实际状况,每组人员不得连续工作超过6 D.现试在实现最大经济效益的目标下,制定对每组工作人员相对公平的风机维护方案.
案例分析
模型假设
1.风电场的风机在其寿命期内会一直运行,不会中途停止.
2.假设不用考虑风向和风机的摆放方向.
3.假设值班人员每次必须连续工作2 D.
4.假设一次一台风机的维修工作时间2d算1个周期.
5.假设值班人员和维修的工作不受任何因素的影响.
模型的建立
为使风电场达到较好的经济效应且维修人员的工作量相对均衡,为简化问题,现将一年分为如下三部分考虑:
第一部分:上半年第1d到第180d,共180d;
第二部分:全年第181d到185d,共5d;
第三部分:第186d到第365d,共180 D.
不妨将维修风机工作全部安排在第一部分与第三部分完成,第二部分只完成值班工作即可,并且在排班第二部分5d时考虑第一第三部分每组工作人员的总排班量,尽量平衡4组人员的总工作量.即将全年的维修工作全部安排在第一、第三两部分完成,每部分均需完成对所有风机进行一次维护.若每次维护风机的顺序不变,则已满足条件:每台风机两次维护时间不得超过270 D.又因每次维护工作需同一组工作人员连续工作2d才能完成,不妨再假设值班人员每次必须连续值班2d,则可将维修、值班两类工作统一.为方便建立模型,可假设每连续的2d为一个工作周期.因为影响电厂效益的主要因素为维修过程中所占用的有效风时数,为使经济效益达到最好,满足维修时总可用风时数尽可能小即可.(https://www.daowen.com)
Xij表示第i组人员在第j个工作周期是否工作,若工作取1,不工作取0,tj表示第一部分每个工作周期所对应的可用风时数,希望满足维修占用的总可用风时数最少这一目标,即
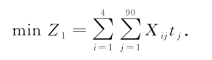
计修完124台风机所需的工作量为124周期;计第一部分的值班工作量为90周期,则第一部分的工作量总和为124+90=214,可得约束条件一:
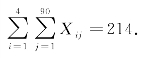
每个组的工作时间不能连续超过6d即连续工作周期不能超过3可得约束条件二:
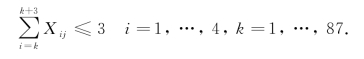
每天风电场均须有值班人员,所以每周期至少有1组人员在工作,得约束条件三:
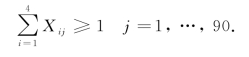
综上,得出如下0~1规划模型:
其中,目标函数为
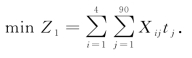
约束条件为
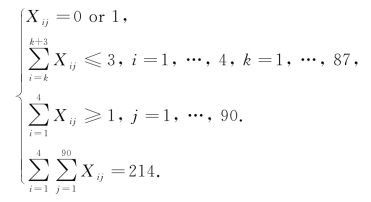
拓展提升:学习完本书后,请用LINGO编程求解上述模型,得出风电场最优排班方案.
