8.2.1 可分离变量微分方程

8.2.1 可分离变量微分方程

定义1

一般形如

的方程，称为变量可分离的微分方程.

这类微分方程可以将两个不同的变量分离在等式的两端，即等式一端只含有一个自变量和其微分，另一端只含有另一个变量和其微分，接着等式两端同时进行积分运算，即可求出通解.称这种方法叫分离变量法.

分离变量法的解法步骤：

（1）分离变量：

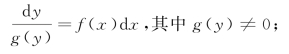
（2）两边同时积分：；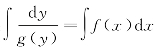

（3）求解不定积分，得通解.

例1 求解微分方程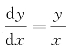的通解.

解 显然y=0是该方程的解.

当y≠0时，方程可变形为，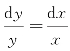

两端同时积分，即

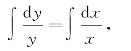
积分后，求解即

化简得

即，由于±仍是任意常数，可记作C，于是，所给方程的通解为y=Cx，其中C为任意常数.

用MATLAB软件求解如下：

例2 求方程xydx-dy=ydx满足初始条件y|x=0=2的特解.

解 整理方程，得

y(x-1)dx=dy.

分离变量，得

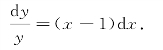
两边积分，得

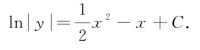
因此，原方程的通解为将初始条件y|x=0=2代入得C=2.

故所求的特解为

用MATLAB软件求解如下：