7.1 不定积分
2026年01月14日
7.1 不定积分
20世纪以来,随着大量的边缘科学诸如电磁流体力学、化学流体力学、动力气象学、海洋动力学、地下水动力学等的产生和发展,相继出现各种各样的微分方程,通过不定积分我们得出这些问题解,从而处理各种科学问题,促进社会发展.
案例1 在几何中的应用
曲线方程 设曲线通过点(1,2),且曲线上任一点处的切线斜率等于这点横坐标的两倍,求此曲线的方程.
解 设所求曲线方程为y=f(x),依题意,曲线上任一点(x,y)处的切线斜率为即f(x)是2x的一个原函数.2x的不定积分为
![]()
因此必有某个常数C使f(x)=x2+C,即曲线方程为y=x2+C曲线族中的某条.
又所求曲线通过点(1,2),故
2=1+C,C=1,
于是所求曲线为
y=x2+1.
案例2 在物理中的应用
结冰厚度 美丽的冰城常年积雪,滑冰场完全靠自然结冰,结冰的速度由![]()
![]() (k>0为常数)确定,其中y是从结冰起到时刻t时冰的厚度,求结冰厚度y关于t的函数.
(k>0为常数)确定,其中y是从结冰起到时刻t时冰的厚度,求结冰厚度y关于t的函数.
解 根据题意,结冰厚度y关于时间t的函数为
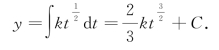
其中常数C由结冰的时间确定.(https://www.daowen.com)
如果t=0时开始结冰的厚度为0,即y(0)=0代入上式得C=0.
这时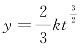 为结冰厚度关于时间的函数.
为结冰厚度关于时间的函数.
案例3 在经济学中的应用
边际成本 已知某公司的边际成本函数![]() ,边际收益函数为
,边际收益函数为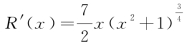 .设固定成本是10000万元,试求此公司的成本函数和收益函数.
.设固定成本是10000万元,试求此公司的成本函数和收益函数.
解 因为边际成本函数为![]() ,所以成本函数为
,所以成本函数为
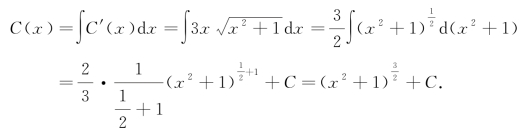
又因固定成本为10000万元,即C(0)=10000(万元),即
![]()
所以C=10000-1=9999(万元).
故所求成本函数为![]() (万元).
(万元).
因为边际收益函数为![]() .所以
.所以
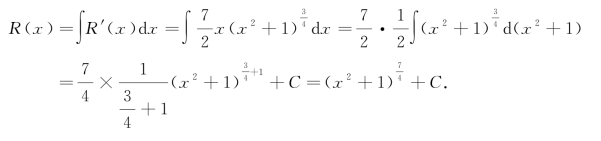
又当x=0时,R(0)=0可得C=-1.
故所求的收益函数为![]()
