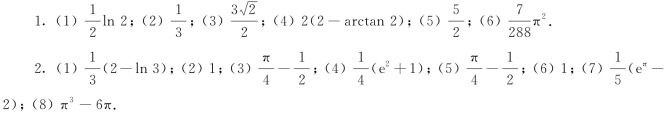7.2.3 定积分的计算
定积分的换元积分法
应用微积分基本公式计算定积分时，首先要求出原函数.本节我们介绍定积分的换元积分，定积分的分部积分以及MATLAB求定积分.
7.2.3.1 定积分的换元法
定理 若（1）函数f（x）在区间[a，b]上连续；
（2）函数x=φ（t）在区间[α，β]上单值有连续导数；
（3）当α≤t≤β时，有a≤φ（t）≤b，又φ（α）=a，φ（β）= B.
在这些条件下，则有定积分的换元公式
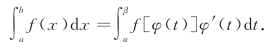
事实上，设F（x）是f（x）的原函数，即F′（x）=f（x）.
由复合函数的求导法则，F[φ（t）]是f[φ（t）]φ′（t）的原函数.由微积分基本公式，得
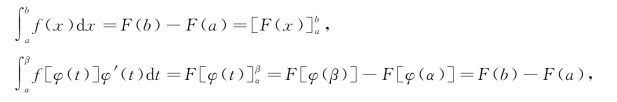
故
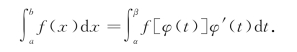
应用定积分换元公式时注意两点：
（1）用x=φ（t）把原来变量x代换成新变量t时，积分的上、下限也要换成相对应于新变量t的积分上、下限，即“换元必换限”；
（2）求出f[φ（t）]φ′（t）的一个原函数F[φ（t）]后，不必像计算不定积分那样再把F[φ（t）]回代成原来变量x的函数，只要把t的上，下限代入F[φ（t）]计算即可.
例1 计算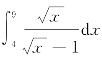
.
解 设x=t，则x=t2，dx=2tdt.
当x=4时，t=2；当x=9时，t=3.
原式：
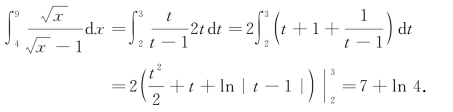
MATLAB代码为：
按Enter得到结果为ans=log（4）+7.
例2 证明
（1）若函数f（x）在区间[-a，a]上连续，且为偶函数（图7-18），则
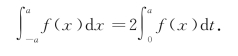
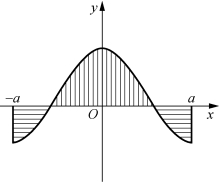
图7-18
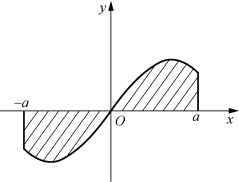
图7-19
（2）若函数f（x）在区间[-a，a]上连续，且为奇函数（图7-19），则
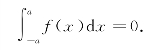
证明 已知
.
对于积分
，
当f（x）为偶函数，有f（x）=f（-x）.令x=-t，则dx=-dt，这时
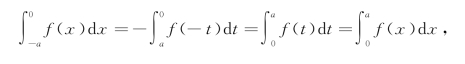
所以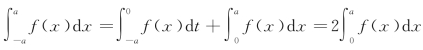 
.
当f（x）为奇函数，有f（x）=-f（-x）.令x=-t，则dx=-dt，这时
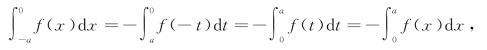
所以
.
例2表明了奇，偶函数在对称区间[-a，a]上的积分性质.利用这一性质，可以简化在对称区间上奇，偶函数的定积分的计算.
例3 计算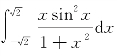
.
解 因为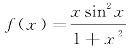
为奇函数，积分区间与原点对称，
所以
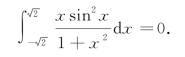
7.2.3.2 定积分的分部积分法
设函数u（x），v（x）在区间[a，b]上有连续导数，由函数乘积的导数公式，有
[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x).
分别求上式两边在[a，b]上的定积分，得(https://www.daowen.com)
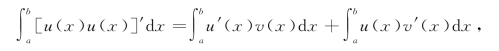
由于
所以有
或简写为
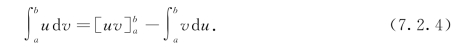
式（7.2.3）或式（7.2.4）都称为定积分的分部积分公式.用分部积分公式求定积分的方法就是分部积分法.
例1 求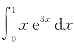
.
解
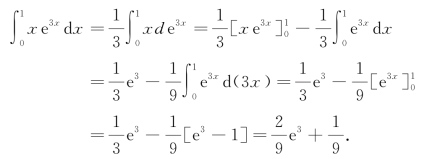
例2 求
.
解
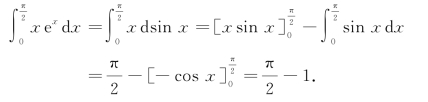
7.2.3.3 MATLAB求定积分
MATLAB中主要用int进行符号积分.
例1 计算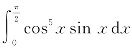
.
解 MATLAB代码为：
按Enter得到结果为ans=1/6.
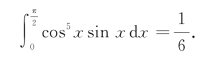
例2 计算
.
解 MATLAB代码为：
按Enter得到结果为ans=pi/16所以：
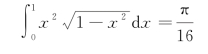
例3 求
.
解 MATLAB代码为：
按Enter得到结果为ans=（pi*2^（1/2））/8+2^（1/2）/2-1.
所以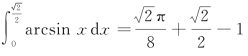
：
例4 求
.
解 MATLAB代码为：
按Enter得到结果为ans=2.
所以
例5 求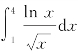
.
解 MATLAB代码为：
按Enter得到结果为ans=log（256）-4.
所以：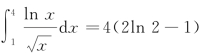
.
课后提升
1.求下列定积分.
2.求下列定积分.
答案
