7.3.1 定积分的微元法
2026年01月14日
7.3.1 定积分的微元法
定积分是分部在区间上的整体量.因整体是由局部组成,将实际问题抽象为定积分,必须从整体着眼,从局部入手.具体作法是,将区间上的整体量化成区间上每一点的微分,也叫微元,这时化整为零,然后,对区间上每一点上的微分无限累加,这是积零为整,这样就得到所求的定积分.我们回顾7.2.1节定积分的概念与性质中曲边梯形面积问题.
设函数f(x)在区间[a,b]上连续且f(x)≥0,由曲线y=f(x)和直线x=a,x=b以及x轴所围成的曲边梯形的面积![]() 的过程:
的过程:
(1)分割:把区间[a,b]任意分成n个子区间,所求曲边梯形的面积A分为每个子区间上小曲边梯形的面积ΔAk(k=1,2,…,n)之和,即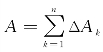 .
.
(2)近似代替:在每个小区间[xk-1,xk]上任取一点ξk(xk-1≤ξk≤xk),以f(ξk)为高,Δxk为底的小矩形的面积为f(ξk)Δxk,则小曲边梯形面积ΔAk的近似值就是小矩形的面积.即ΔAk≈f(ξk)Δxk(k=1,2,…,n).
(3)求和:
![]()
(4)取极限:
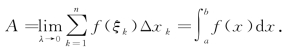 (https://www.daowen.com)
(https://www.daowen.com)
在实际应用中,还可以简化上述步骤:
设函数f(x)在区间[a,b]上连续,具体问题中所求的量为A.
①在区间[a,b]内任取子区间[x,x+Δx],在此子区间上量A的微元为
dA=f(x)dx.
②把微元在区间[a,b]上积分,即
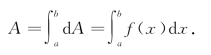
这种方法就是微元法(或元素法).
从上述例子可以看出,要将某实际问题抽象为定积分,首先求出要求量的微元.如计算曲边梯形的面积要求出面积微元.微元都是根据具体问题的公式写出来的.再将每一点上的微元连续累加起来,就得到了定积分.
