9.2.3 假设检验
统计推断的另一类重要问题是假设检验问题.在总体的分布函数完全未知或只知其形式但不知其参数的情况,为了推断总体的某些性质,提出某些关于总体的假设.例如,提出总体服从泊松分布的假设,对于正态总体提出数学期望等于μ0的假设等.假设检验就是根据样本对所提出的假设做出判断:是接受还是拒绝.这就是所谓的假设检验问题.
原假设H0:在统计学中,把需要通过样本去推断正确与否的命题,称为原假设,又称零假设.它常常是根据已有资料或经过周密考虑后确定的.
备择假设H1:与原假设对立的假设.
显著水平(significantlevel)α:确定一个事件为小概率事件的标准,称为检验水平,亦称为显著性水平.通常取α=0.05,0.01.
1.单个总体N(μ,σ2)均值μ的检验,假设检验有三种:
双边检验:H0:μ=μ0,H1:μ≠μ0;
右边检验:H0:μ≤μ0,H1:μ>μ0;
左边检验:H0:μ≥μ0,H1:μ<μ0.
假设检验的基本步骤:
(1)提出假设:原假设H0及备择假设H1;
(2)选择适当的检验统计量,并指出H0成立时,该检验统计量服从的抽样分布;
(3)根据给定的显著水平,确定相应的临界值,并确定拒绝域;
(4)根据样本观察值计算检验统计量H0.当检验统计量的值落入拒绝域时拒绝H0而接受H1,否则可接受H0;
(5)利用P值进行检验的准则,见表9-21.
若P值<α,拒绝H0成立,若P值>α,接受H0成立.
表9-21 P值说明

例5 某车间用一台包装机包装糖果.包得的袋装糖重是一个随机变量,它服从正态分布.当机器正常时,其均值为0.5kg,标准差为0.015kg.某日开工后为检验包装机是否正常,随机地抽取它所包装的糖9袋,称得净重为(kg):0.497/0.506/0.518/0.524/0.498/0.511/0.520/0.515/0.512(α=0.05),问机器是否正常?
解 总体σ已知,x~N(μ,0.0152),μ未知.提出假设:H0:μ=μ0=0.5和H1:μ≠0.5.
①定义变量x,输入数据;正态性检验:P-P图(图9-2);
②选择分析→比较均值→单个样本t检验;
③将变量x放置检验变量栏中,并在检验值输入数据0.5;
④单击确定按钮执行,所得结果见表9-22和表9-23.
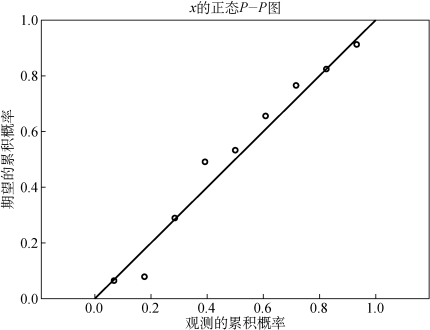
图9-2 正态检验P-P图(https://www.daowen.com)
表9-22 单个样本统计量

表9-23 单个样本t检验

结果表明,图9-2中的P-P图成一条直线是正态分布.根据表9-22可看出样本的均值和标准差,根据表9-23所示双边P值=0.007<α=0.05,所以拒绝原假设,即认为这天包装机工作不正常.
例6 某种电子元件的寿命x(以h计)服从正态分布,μ,σ2均未知.现得16只元件的寿命如下:159/280/101/212/224/379/179/264/222/362/168/250/149/260/485/170(α=0.05),问是否有理由认为元件的平均寿命大于225(h)?
解 提出假设:H0:μ≤μ0=225和H1:μ>225.
操作步骤同上,检验值输入225.
表9-24 单个样本检验

根据表9-24表明,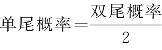 .该题是单尾概率,所以单尾
.该题是单尾概率,所以单尾![]() 0.257,说明在显著水平为0.05的情况下,不能拒绝原假设,认为元件的平均寿命不大于225h.
0.257,说明在显著水平为0.05的情况下,不能拒绝原假设,认为元件的平均寿命不大于225h.
例7 在平炉上进行一项试验以确定改变操作方法的建议是否会增加钢的得率,试验是在同一平炉上进行的.每炼一炉钢时,除操作方法外其他条件都尽可能做到相同.先用标准方法炼一炉,然后用建议的新方法炼一炉,以后交换进行,各炼了10炉,其得率分别为

设这两个样本相互独立分别来自正态总体N(μ1,σ2),N(μ2,σ2),μ1,μ2,σ2均未知,问建议的新方法能否提高得率(α=0.05)?
解 总体σ已知,x~N(μ,0.0152),μ未知.提出假设:H0:μ1-μ2≥0和H1:μ1-μ2<0.
(1)定义变量x,g,输入数据;
(2)选择分析→比较均值→独立样本t检验;
(3)将变量x放置检验变量栏中,将g放入分组变量,定义g的取值并在检验值;
(4)单击确定按钮执行,所得结果见表9-25和表9-26.
表9-25 组统计量

表9-26 独立样本检验
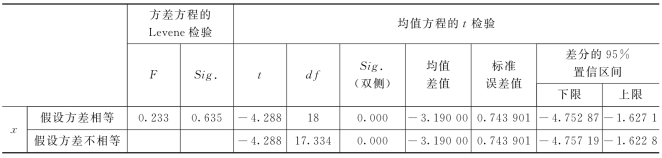
根据表9-25和9-26假设方差相等和不相等的情况下,双尾P值=0.000<α=0.05表明在α=0.05的显著水平下,可以拒绝原假设,即认为建议的新操作方法较原方法优.
