8.5 二阶常系数线性微分方程

8.5 二阶常系数线性微分方程

微分方程在化学方面的应用

案例电容器放电问题

一个电阻R=90Ω，电感L=10H，电容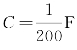组成的串联电路，如图8-2所示，当开关K闭合后，电容器开始放电，如果电容器上原有电量为1C，试分析电容器放电规律.

解 设任意时刻电容器电量为Q=Q（t）.电流即为

i=Q′(t).

由闭合回路上电压的代数和等于零得

Uc+UL+UR=0,

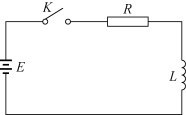
图8-2

其中，

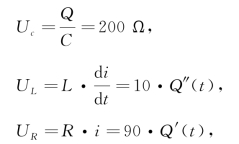
则

200·Q+10·Q″(t)+90·Q′(t)=0,

即

20·Q+Q″(t)+9·Q′(t)=0.

对应的特征方程为

r2+9·r+20=0.

特征根为

r1=-4,r2=-5.

故通解为

Q=C1e-4t+C2e-5t.

求导得

Q′=-4·C1e-4t-5·C2e-5t.

将初始条件

Q|t=0=1,Q′|t=0=0,

代入上式有

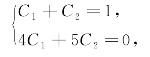
即

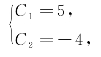
解为

Q=5·e-4t-4·e-5t,

因此，电容器放电规律为Q=5·e-4t-4·e-5t.

MATLAB解法如下：