第4章 恶臭污染的散逸收集及输送
恶臭的散逸特性属于流体力学的研究范畴,而流体力学的最终目的是寻求满足给定边界条件的流动状态。对于空间坐标(x、y、z)和时间t这四个独立变量,对应有五个未知标量函数,分别为流体的速度矢量V(三个分量u、v、w)和热力学量(压力p、温度T、内能e、焓h、熵s等)中的任意两个量。在热力学状态方程中,只有两个物理量能够独立变化。为了求解这五个未知量,需要寻求五个相互独立的约束方程,通常可从三大守恒定律(质量守恒定律、动量守恒定律和能量守恒定律)出发得到。由于动量是空间矢量,故动量守恒定律将给出三个包含未知量的关系式,另外两个关系式则由质量守恒定律和能量守恒定律给出。由此,五个未知量与五个关系式构成封闭的方程组,理论上可根据定解条件的限制求得所研究问题的特解。
根据质量守恒定律,指定质点系的质量不随时间的推移而发生变化,即流体在流动过程中,对于任一指定的控制体,单位时间内流入该区域的质量等于流出该区域的质量。其控制方程为
![]()
式中 ρ——密度;
u——速度矢量沿x轴方向的分量;
v——速度矢量沿y轴方向的分量;
w——速度矢量沿z轴方向的分量。
引入拉普拉斯算子(∇),方程(4-1)可表示为
![]() (https://www.daowen.com)
(https://www.daowen.com)
拉普拉斯算子:
![]()
方程(4-2)是直角坐标系下连续性方程的偏微分方程形式。对于柱面坐标系,连续性方程的形式为
![]()
在经典力学中,物体的运动状态是用牛顿第二定律进行描述的,即F=ma。该基本物理学原理同样适用于流体系统中,对于流体通常采用牛顿第二定律的另一种表述形式——动量守恒定律,即流体系统的动量变化率等于该系统受到的外力之和。进一步考虑作用在单位质量黏性流体上的力,除了质量力F0=(X,Y,Z)外,还有周围流体施加的表面应力(法向和切向)。因而动量方程可表述为
![]()
根据能量守恒定律,单位时间内任意指定物质系统总能量的增加量恒等于外界对该系统所做的功与传入的热量之和。对于单位质量流体,其所具有的总能量包括内能e和动能![]() 。其中,
。其中,![]() 。若令
。若令![]() ,则单位质量流体的能量变化率为
,则单位质量流体的能量变化率为![]() 由此可得应用于流体的能量守恒方程
由此可得应用于流体的能量守恒方程
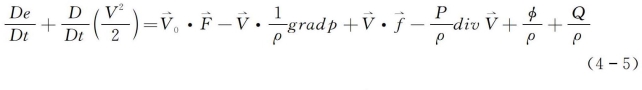
以上流体力学控制方程中,设流体的速度矢量 在三个坐标上的分量分别是u、v、w,压力为p,密度为ρ,内能为e,流体摩擦产生的热为φ,由外界传入的热量为Q。
在三个坐标上的分量分别是u、v、w,压力为p,密度为ρ,内能为e,流体摩擦产生的热为φ,由外界传入的热量为Q。
